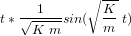Les CubeSats
Auteur: Gary Quinsac
- Découvrir
- Projet spatial
- Intérêt des satellites
- Classes de satellites
- Système spatial
- Conception, exigences et contraintes
- Déroulement d'un projet spatial
- Nanosatellites
- Standard CubeSat
- Applications pour les CubeSats
- Sous-systèmes
- Exemples de missions CubeSats
- Système de Contrôle d'Attitude et d'Orbite
- Introduction au Système de Contrôle d'Attitude et d'Orbite
- Système de Contrôle d'Attitude
- Système de Guidage, Navigation et Contrôle
- Modes SCAO
- Comprendre
- Réferentiels et transformations
- Systèmes de coordonnées
- Généralités
- Systèmes de coordonnées célestes
- Systèmes de coordonnées spatiaux
- Représentation d'attitude
- Introduction
- Matrice du cosinus directeur
- Angles d'Euler
- Quaternions
- Représentation 3D
- Présentation mathématique
- Equations du mouvement
- Introduction à la cinématique et la dynamique
- Cinématique du satellite
- Cinématique du point
- Cinématique d'attitude
- Dynamique du satellite
- Bases de la dynamique
- Dynamique du solide
- Perturbations
- Perturbations : introduction
- Perturbations externes
- Champ magnétique
- Gradient de gravité
- Pression de radiation solaire
- Traînée atmosphérique
- Perturbations internes
- Matériel
- Introduction aux capteurs et actionneurs
- Capteurs
- Capteurs optiques
- Capteurs magnétiques
- Capteurs inertiels
- Actionneurs
- Actionneurs inertiels
- Actionneurs magnétiques
- Propulsion
- Introduction à la propulsion
- Fondamentaux de la propulsion
- Systèmes de propulsion
- Systèmes de propulsion
- Propulsion chimique
- Propulsion électrique
- Filtrage et lois de commande
- Introduction
- Estimation d'attitude
- Principe
- Cas statique
- Cas général
- Lois de contrôle
- Introduction à la théorie du contrôle
- Contrôleur
- Se tester
- Présentation des exercices
- QCM sur la partie "découvrir"
- Exercices : Représentation d'attitude
- Exercices : Equations du mouvement
- Exercice : Couples perturbateurs sur un CubeSat
- Exercice : Propulsion
- Exercices : Lois de commande
- Mini-projets
- Présentation des mini-projets
- Questions
Les CubeSats
Ce cours est une introduction aux problématiques liées à la réalisation d'une mission spatiale. Pour ce-faire, nous vous proposons d'aborder un format bien particulier de petits satellites : les CubeSats. D'une manière générale, le bon fonctionnement d'un satellite est garanti par de nombreux domaines qui seront introduits dans ce cours. Dans un second temps, nous nous focaliserons sur un aspect en particulier, la nécessité de fournir un contrôle d'attitude et d'orbite pour mener à bien une mission spatiale. Des exercices vous permettront de vous exercer sur de nombreux points du cours. Enfin, vous pourrez utiliser les connaissances acquises pour pré-dimensionner quatre missions spatiales qui vous sont proposées sous la forme de mini-projets.
 Prérequis
Prérequis
La partie Découvrir s'adresse à toute personne, pas nécessairement scientifique, qui souhaiterait découvrir brièvement les aspects et enjeux d'une mission spatiale. Pour aborder la partie Comprendre, un bagage scientifique de niveau licence est requis, à savoir :
- Algèbre linéaire : maîtrise des produits scalaire et vectoriel, des opérations sur les matrices;
- Géométrie dans l'espace à 3 dimensions : notions sur les référentiels et systèmes de coordonnées;
- Mécanique classique :
- connaissance du mouvement linéaire et de la 2ème loi de Newton (leurs équivalents pour des mouvements circulaires seront introduits dans le cours mais des notions préalables peuvent aider);
- connaissance des forces de gravité, de pression, de frottement et électromagnétique.
- Automatisme et filtrage : des notions dans ces deux domaines faciliteront la compréhension de la dernière partie de ce cours.
Tout au long de ce cours le lecteur doit garder à l'esprit que de nombreuses notions abordées pourraient faire l'objet d'un cours à part entière. Des liens vers d'autres cours issus de ce site ou de Fenêtre sur l'univers seront proposés autant que possible. Voici également des références qui pourront lui permettre d'approfondir les sujets souhaités :
 Livres conseillés
Livres conseillés
- M. Macdonald and V. Badescu, The International Handbook of Space Technology, Springer, 2014.
- F. L. Markley and J. L. Crassidis, Fundamentals of Spacecraft Attitude Determination and Control, vol. 2. New York, NY: Springer New York, 2014.
- M. J. Sidi, Spacecraft Dynamics and Control, vol. 7, no. 9. Cambridge: Cambridge University Press, 1997.
[Début du cours]
Découvrir
Auteur: Gary Quinsac
Projet spatial
Auteur: Gary Quinsac
Intérêt des satellites
Besoin scientifique
L'astronomie est science d'observation. Dans l'Antiquité, l'observation des objets célestes visibles à l’œil nu permet d'abord la mesure du temps. Ensuite, elle s'attache à prédire les mouvements des objets observés. Les observations étaient menées par des astrologues (qui parlent des astres) qui, au fil du temps, ont évolué pour travailler comme astronomes (qui étudient le mouvement des astres) et, aujourd'hui, astrophysiciens (qui utilisent la physique pour comprendre les astres). Au cours des siècles les instruments utilisés s'améliorent, permettant des observations toujours plus fines. Le XXème siècle marque un tournant, les astronomes se retrouvant confrontés à des limitations difficilement surmontables ainsi qu'à des besoins nouveaux :
- de nombreuses longueurs d'onde ne sont pas accessibles depuis le sol car elles sont absorbées par l'atmosphère de notre planète ;
- la pollution atmosphérique limite la précision des instruments au sol ;
- la turbulence atmosphérique dégrade les images astronomiques ;
- on commence à vouloir effectuer des observations géophysiques et géographiques de notre planète pour la météorologie, la géodésie, la climatologie, l'inventaire des ressources naturelles, la reconnaissance militaire…);
- enfin, un besoin de grands relevés à l'échelle de toute la planète apparaît.
Pour certains objectifs, il apparaît alors nécessaire de satelliser les instruments d'observation.
Différentes applications actuelles
Dès le début de l'ère spatiale, les industriels emboîtent le pas des scientifiques et imaginent des applications commerciales. On retrouve ainsi, de nos jours, de nombreux types de satellites différents :
- satellites astronomiques, dédiés à l'observation d'objets spatiaux de l'Univers proche ou lointain. On peut citer le télescope spatial infrarouge Herschel et la mission de cartographie de notre galaxie Gaia, tous deux de l'agence psatiale européenne (ESA), ou encore le chasseur d'exo-planètes Kepler de l'agence spatiale américaine (NASA) ;
- satellites de communication, qui répondent à des besoins de télécommunication, tels que ceux d'Intelsat, premier fournisseur de services de télécommunication par satellites en 2008 ;
- satellites d'observation de la Terre, à visée non-militaire telles que la surveillance environnementale, la météorologie ou encore la cartographie. La famille de satellites SPOT développées par l'agence spatiale française (CNES) en fait partie ;
- satellites de positionnement et de navigation servant à localiser des récepteurs au sol. À titre d'exemple, nous pouvons citer les systèmes américain GPS, européen GALILEO et russe GLONASS ;
- vaisseaux spatiaux habités, comme la famille de véhicules spatiaux soviétiques puis russes Soyouz ;
- stations spatiales, qui sont des structures artificielles développées pour que des humains puissent vivre dans l'espace. À la différence des véhicules spatiaux habités, celles-ci ne disposent pas d'un moyen de propulsion principal. La Station Spatiale Internationale (ISS) en est un exemple.
 Aller plus loin
Aller plus loin
Opacité atmosphérique
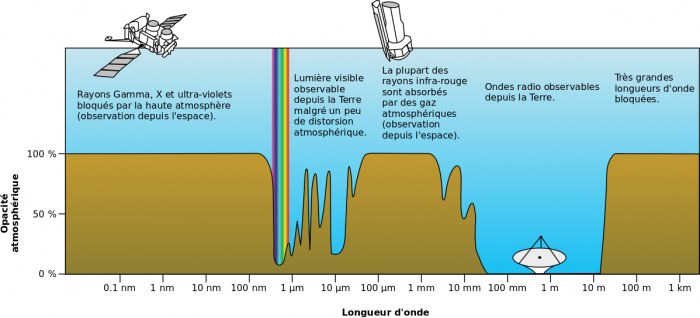
Pourcentage d'absorption du spectre électromagnétique par l'atmosphère terrestre. Si l'atmosphère est opaque à une grande partie du spectre électromagnétique, parmi les exceptions se trouve le domaine du visible.
Crédit :
NASA
Turbulence atmosphérique et optique adaptative

Effets liés à turbulence atmosphérique. L'image de gauche est l'étoile HIC 59206 capturée par le VLT, tandis que celle de droite est la même image corrigée par
optique adaptative.
Crédit :
European Southern Observatory
Météorologie

L'ouragan Matthew vu dans l'infrarouge par le satellite Metop-A, le 7 octobre 2016. Les observations dans plusieurs bandes spectrales conduisent, une fois compilées, à une carte de température.
Crédit :
Eumetsat
Classes de satellites
Les satellites sont généralement classés en fonction de leur masse au lancement. Alors que dans les années 60, lorsque l'affrontement politique entre les États-Unis et l'Union soviétique s'exprimait sur le terrain de la course à la Lune, les engins spatiaux n'étaient limités que par les progrès techniques de l'époque, ce sont actuellement des critères économiques qui prévalent lors du développement des satellites. Une relation à peu près linéaire existe entre la masse d'un satellite et son coût. Une classification typique des satellites est présentée dans le tableau suivant.
Classification des satellites
| Dénomination | Masse | Coût | Examples |
|---|
| Gros satellites | > 1 t | > 150 M€ | Station Spatiale Internationale (500 t) |
| Sondes spatiales : Cassini Huygens autour de Saturne (NASA, 5,7 t) / Rosetta autour d'une comète (ESA ,3 t) |
| Satellites GEO de 3 à plusieurs dizaines de tonnes |
| Satellites LEO, MEO et GEO de 1 à 3 tonnes |
| Satellites moyens | <1 t | < 150 M€ | Constellation de télécommunication Iridium en LEO (66 satellites, 700 kg) |
| Télescope spatial CoRoT pour l'étude des étoiles (CNES, 668 kg) |
| Constellation Galileo, système de positionnement par satellites (ESA, 700 kg) |
| Minisatellites | < 500 kg | < 50 M€ | Sondes spatiales : New Horizons vers Pluton (NASA, 478 kg, ~600 M€) / SMART-1 vers la Lune (ESA, 366 kg, ~110 M€) |
| Plateforme PROTEUS (Thalès) |
| Microsatellites | < 100-150 kg | < 8 M€ | Plateforme Myriade (CNES, 100-150 kg) : PARASOL pour l'étude de l'atmosphère terrestre / MICROSCOPE pour le test du principe d'équivalence |
| PROBA-1 : démonstrateur technologique (ESA, 94 kg) |
| Nanosatellites | < 10 kg | < 3 M€ | Constellation Planet Labs (60 CubeSats 3U de 5 kg début 2017), observation de la Terre |
| GOMX-1 : CubeSat 2U (GomSpace 2,66 kg), démonstrateur technologique |
| ROBUSTA-1A (CNES / Université de Montpellier 2) : CubeSAT 1U (1 kg) développé par des étudiants |
| Picosatellites, femtosatellites... | < 1 kg | < 300 k€ | WREN (STADIKO) : femtosatellite de démonstration technologique financé participativement |
 Source d'information
Source d'information
Masse et coûts de quelques satellites
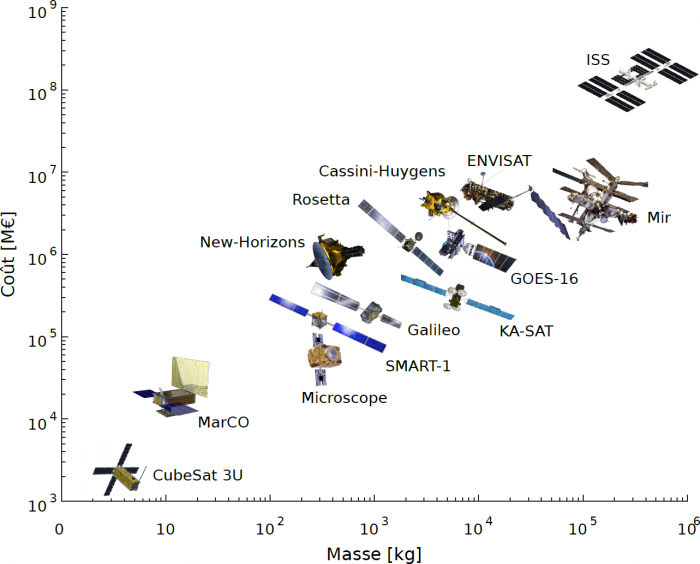
Comparaison de la masse et du coût de certains satellites. Les deux paramètres sont reliés par une relation presque linéaire, les satellites scientifiques apparaissant plus coûteux.
Crédit :
Gary Quinsac
Hubble

Télescope spatial Hubble. Sa masse est de 11 tonnes, il fait la taille d'un bus (13 x 4 x 4 m3) et consomme 2,8 kW. Son orbite relativement basse (550 km d'altitude) a permis aux navettes spatiales américaines de venir effectuer des réparations et des remplacements d'équipements.
Crédit :
ESA
Station Spatiale Internationale

Plus grand objet artificiel placé dans l'espace (110 m de longueur, 74 m de largeur et 30 m de hauteur), la Station Spatiale Internationale fait environ 400 tonnes. Chacune de ses 16 ailes de panneaux solaires mesure 35 m de long pour 12 m de large, produisant un maximum de 120 kW. Son altitude varie entre 330 et 420 km et a été choisie pour faciliter son assemblage/ravitaillement en orbite par les différents pays impliqués dans son exploitation.
Crédit :
CNES
Satellite GPS

Un satellite GPS de 1,5 tonne pour 2.5 x 2 x 2 m3. Il consomme 1,9 kW et orbite à 20000 km d'altitude. De nombreux satellites de ce type composent ce qu'on appelle une constellation GPS, l'objectif étant d'avoir toujours au moins 4 satellites en visibilité depuis une zone donnée à la surface de la Terre.
Crédit :
GPS.gov
Satellite de télécommunication

Satellite de télécommunication KA-SAT d'une masse de 6 tonnes (dont 3 pour le carburant) et mesurant 5 x 2 x 2 m3. Comme de nombreux satellites de télécommunication il se trouve sur l'orbite géostationnaire (GEO), c'est à dire à 36000 km d'altitude. Ses panneaux solaires de 40 m d'envergure lui permettent de produire 14,4 kW.
Crédit :
J. Huart/ ESA
Système spatial
Un système spatial se décompose en trois éléments :
- le segment spatial,
- le segment sol,
- le lancement,
Segment spatial
Le segment spatial est décomposé en deux sous-ensembles principaux : la charge utile et la plateforme. La charge utile regroupe les instruments nécessaires à la réussite de la mission. Cela va du montage optique pour un satellite d'observation tel que Hubble aux antennes et amplificateurs associés pour un satellite de télécommunication. Il est important de remarquer que c'est la charge utile d'un satellite qui définit sa mission. La plate-forme assure les servitudes, c'est-à-dire l'ensemble des fonctions génériques nécessaires à l'activité en orbite. Ses différentes fonctions sont :
- la structure porteuse,
- le contrôle thermique,
- la génération, le stockage et la distribution d'énergie,
- la télécommunication,
- la télémesure, la télécommande et la localisation,
- le traitement, le stockage et la gestion des données à bord,
- le contrôle d'attitude et d'orbite,
- la propulsion.
Ces aspects sont developpés plus en détail dans la partie consacrée aux sous-systèmes.
Segment sol
Le segment sol se compose des stations de poursuite, des moyens d'opération et de commande/contrôle et des moyens de programmation de la charge utile, de réception, pré-traitement, archivage et diffusion des informations de cette même charge utile (centre de mission).
Lancement
Le lancement est l'étape permettant la mise en orbite d'un objet. C'est une étape dimensionnante en termes d'orbite atteinte, de masse et de volume disponibles sous coiffe. Le lanceur le plus lourd jamais créé a permis à un homme de marcher sur la Lune pour la première fois en 1969 et se nomme Saturn V. Depuis, de très nombreux types de lanceurs ont été développés pour permettre à des charges utiles plus ou moins importantes d'atteindre différentes orbites.
Les différentes orbites terrestres sont classées en fonction de leurs altitude, inclinaison et excentricité. En voici quelques unes :
- basses ou LEO pour "Low Earth Orbit", ces orbites présentent l'avantage de permettre des révolutions rapides et d'être sous les ceintures de Van Allen dont elles ne subissent pas les particules énergétiques ;
- héliosynchrones ou SSO pour "Sun Synchronous Orbit", elles sont choisies spécifiquement pour que l'angle entre le plan d'orbite et la direction du Soleil reste quasiment constant, ce qui permet notamment d'éviter les phases d'ombre dues à la Terre ;
- moyennes ou MEO pour "Medium Earth Orbit", privilégiées par les satellites de navigation (GPS, Glonass, Galileo) ;
- très elliptiques ou HEO pour "Highly Elliptical Orbit", elles sont utilisées pour permettre à des satellites de passer une longue période, autour de son apogée, au dessus de zones du globe à forte latitude ;
- de transfert géostationnaire ou GTO, pour "Geostationary Transfert Orbit", pour rejoindre une orbite géostationaire depuis une orbite basse ;
- géostationnaires ou GEO pour "Geostationary Earth Orbit", pour orbiter en 24h et ainsi pouvoir se trouver en permanence au-dessus du même point sur la Terre au voisinage de l'équateur.
- lointaines ou interplanétaires; elles regroupent les trajectoires de rencontre avec la Lune ou d'autres corps de notre système solaire, ainsi que des zones d'équilibre gravitationnel stables nommées points de Lagrange.
 Ceintures de Van Allen
Ceintures de Van Allen
Les ceintures de Van Allen, ainsi nommées en l'honneur du physicien les ayant découvertes, sont des zones de la magnétosphère terrestre contenant une grande densité de particules énergétiques, pour la plupart d'origine solaire. Leurs deux principaux effets sont la création d'aurores polaires lorsque les particules énergétiques rencontrent l'atmosphère terrestre et la mise en danger des satellites les traversant (des blindages sont nécessaires pour protéger les équipements sensibles de satellites passant une longue période dans les ceintures). On a pour habitude de considérer qu'elles sont au nombre de deux, la première s'étendant entre 700 km et 10 000 km d'altitude et la seconde entre 13 000 km et 65 000 km. D'autres ceintures sont susceptibles d'apparaître mais ne semblent pas permanentes.
Station sol de PicSat

Station sol UHF/VHF installée à l'Observatoire de Meudon pour communiquer avec le CubeSat PicSat.
Crédit :
PicSat
Comparaison de lanceurs
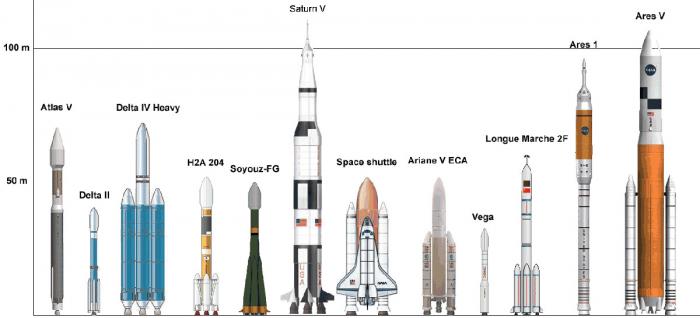
Comparaison de lanceurs utilisés depuis le début de l'ère spatiale. La masse de carburant embarqué par un lanceur pour satelliser un objet représente la majeure partie de sa masse au lancement. Par exemple, l'Ariane 5 GS est capable d'emporter plus de 6 tonnes en orbite GTO, elle mesure à peu près 50 m de hauteur pour une masse au décollage de 750 tonnes composée à 90% de carburant.
Crédit :
NASA
Orbites terrestres
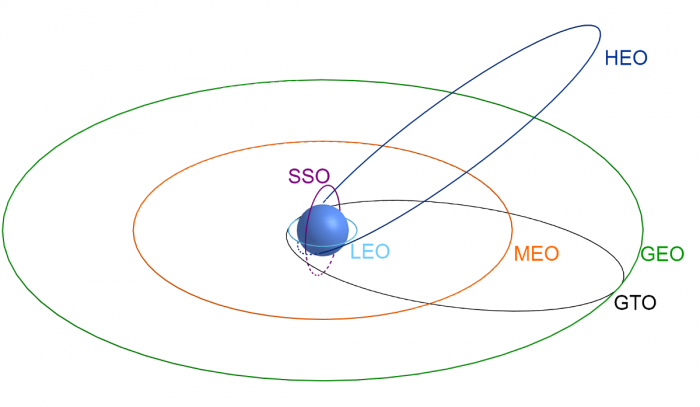
Orbites terrestres les plus utilisées.
Crédit :
Gary Quinsac
Aurore boréale

Photo d'une aurore boréale en Alaska. Ces phénomènes lumineux sont provoqués par la rencontre entre des particules énergétiques provenant du Soleil ou du rayonnement cosmique et de l'atmosphère. Ces particules ont été préalablement piégées par le champ magnétique terrestre dans une zone que l'on nomme ceinture de Van Allen.
Conception, exigences et contraintes
Tout projet spatial répond à un enjeu : objectif scientifique, démonstration technologique... Il doit donc faire face à son lot d'exigences et de contraintes. Les exigences définissent les fonctions qu'un système ou un composant doit remplir. Elles répondent à la question "que fait ce système/composant ?". Les contraintes spécifient, quant à elles, ce que le système doit être. Elles sont généralement des limitations du système.
Cette situation est encore plus vraie pour les projets spatiaux. Les erreurs commises sont le plus souvent irréversibles et irratrapables une fois que le système est lancé. Il faut ainsi :
- remplir des exigences mission,
- prendre en compte toutes les contraintes technologiques, d'environnement spatial, de lancement et des moyens sols,
- respecter les règlements,
- proposer des compromis performance/coûts et d'éventuelles modifications des exigences.
Les exigences mission dépendent du type de satellite considéré, mais le principe est toujours le même : un besoin est exprimé auquel le satellite va essayer de répondre. Se faisant, un type d'orbite va être identifié :
- terrestre : basse, héliosynchrone, géostationnaire, excentrique ;
- non-terrestre : au point de Lagrange, solaire, interplanétaire.
De ce choix découle un système de lancement, ou lanceur. La charge utile embarquée doit ensuite répondre aux exigences mission tout en prenant en compte les contraintes imposées par le système de lancement (volume et masse disponibles, interfaces) et l'environnement orbital. Toutes ces questions se posent bien entendues également pour la plate-forme, qui devra s'adapter à la charge utile choisie (ou inversement, si le choix est fait d'utiliser une plate-forme standardisée).
L'environnement spatial présente de nombreuses spécificités qui doivent être prises en compte dès le début du développement :
- le vide,
- l'apesanteur,
- les forts contrastes de température et l'absence de convection thermique,
- les effets des rayonnements électromagnétiques et des particules chargées énergétiques,
- la présence d'oxygène atomique qui est un agent chimique agressif,
- la collision possible avec des débris ou des micrométéorites,
- l'impossibilité d'accéder au satellite une fois en orbite (sauf cas exceptionnel).
Outre ces aspects négatifs, l'environnement peut également être mis à profit pour certaines fonctions :
- contrôler l'attitude avec le gradient de gravité, la pression de radiation solaire ou le champ magnétique local,
- contrôler l'orbite avec le freinage atmosphérique,
- refroidir des composants avec le fond du ciel à 3 K.
Que le programme soit public ou privé, la question du coût reste centrale. Ce coût doit prendre en compte le lancement, le segment spatial (durée de fabrication, des essais…), le système sol et des opérations. Il est ensuite amorti sur la durée de vie du système.
Des règlements nationaux et internationaux imposent des restrictions, notamment en termes de fréquences de télécommunication. La bande de fréquence utilisée doit avoir été définie en amont. Dans certains cas (satellite GEO) la notion de compatibilité électromagnétique implique de ne pas perturber les satellites voisins. La gestion d'un satellite en fin de vie est de plus en plus importante du fait de la prolifération des débris en orbite terrestre. Ainsi en France, la Loi sur les Opérations Spatiales (LOS) réglemente ces aspects.
 Exemple : pollution orbitale
Exemple : pollution orbitale
En orbite autour de la Terre, les objets sont animés de vitesses relatives qui peuvent atteindre 15 à 20 km/s. À de telles vitesses, les énergies cinétiques qui sont en jeu peuvent engendrer de très importants dégâts. Chaque collision, au même titre que le délitement des vieux satellites, crée de nouveaux débris qui viennent augmenter le nombre d'objets orbitant la Terre. Cette pollution orbitale croît très fortement et impose aux États et aux entreprises de mettre en place des stratégies de réduction du nombre de débris.
Classification des débris orbitaux et risques associés
| Taille de l'objet | Nombre d'objets | Répertoriés ? | Risques associés à l'objet |
|---|
| > 10 cm | 20 000 | Oui | Collisions catastrophiques, production de débris |
| 1 cm < objet < 10 cm | 500 000 | Non | Perte de la mission, aucun blindage ne résiste à des objets > 2 cm |
| < 1 cm | > 10 000 000 | Non | Perforations, risque de perte d'équipement critique |
Arbre fonctionnel
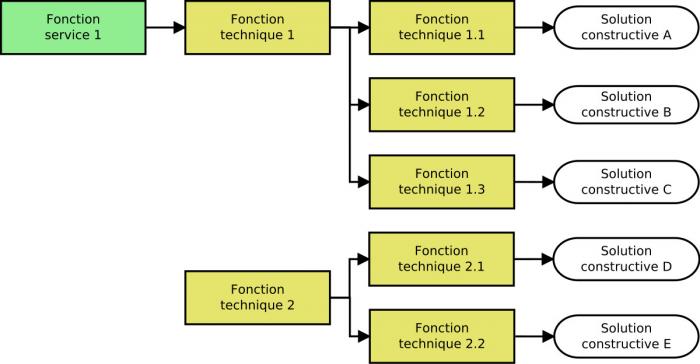
Exemple d'arbre fonctionnel. A partir des fonctions principales sont dérivées des fonctions secondaires, jusqu'à pouvoir identifier des solutions exécutant ces fonctions.
Crédit :
Gary Quinsac
Nombre mensuel d'objets en orbite terrestre par type d'objets
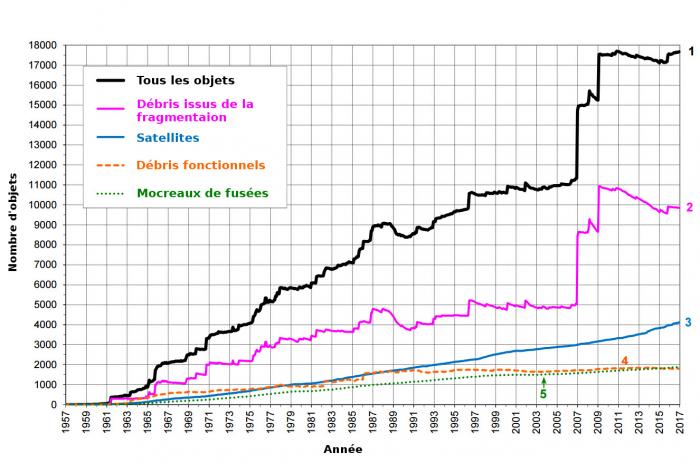
Résumé de tous les objets en orbite terrestre officiellement répertoriés par l'U.S. Space Surveillance Network. Les "débris issuent de la fragmentation" regroupent les débris produits par des anomalies (explosions, casses...), tandis que les "débris fonctionnels" regroupent l'ensemble des objets libérés, distribués ou séparés dans le cadre d'une mission. Les "morceaux de fusée" quant à eux sont des pièces ou des ensembles de pièces appartenant à la fusée (tels que les différents étages de poussée). Le pic observé en 2007 correspond à la destruction par la Chine de l'un de leurs satellites météorologiques (Fengyun-1C) dans le cadre d'un test de missile anti-satellite. Le second, en 2009, est dû à la collision entre un satellite militaire russe hors de service (Cosmos 2251) et un satellite de télécommunication américain (Iridium 33).
Crédit :
NASA - Orbital Debris Quarterly News, February 2017
Déroulement d'un projet spatial
Cycle de vie d'un système
Au cours d'un projet, un système va être amené à évoluer, d'un premier état conceptuel à un état physique. Des tests doivent alors êtres effectués pour s'assurer que le système répond aux exigences identifiées précédemment, ce sont les étapes de validation. Les états successifs du système et les activités le concernant constituent ce que l'on appelle le cycle de vie. S'il existe différentes façons de représenter ce-dernier, le cycle en V reste le modèle le plus suivi. Ce cycle est parcouru de gauche à droite, d'abord du haut vers le bas puis du bas vers le haut. Aux phases de conception succèdent les phases d'assemblage, d'intégration et de test. Le cycle en V permet d'identifier facilement l'étape de validation correspondant à chaque étape de conception.
Dans certains projets, tels que des projets étudiants, on utilise des méthodes agiles. Elles ont pour origine le manifeste Agile et reposent sur un cycle de développement itératif, incrémental et adaptatif. Ces méthodes autorisent une plus grande flexibilité et réactivité, nécessaires à ces projets.
Phases d'un projet spatial
Dans le cas d'un projet spatial, on divise le déroulement du projet en 7 phases successives. Chacune d'entre-elles correspond à un état du système et se conclut par une revue de projet. On peut remarquer que les premières phases correspondent aux étapes de conception (0-A-B), avant de passer à la réalisation (C-D), à l'utilisation et au retrait.
- Durant la phase 0, on exprime la mission en termes de besoin, on évalue l'environnement et ses contraintes et on identifie des concepts possibles.
- La phase A sert à affiner et valider le besoin. Les différents concepts possibles sont ainsi explorés, on identifie et évalue les éléments critiques afin d'estimer les risques associés.
- Durant la phase B l'architecture système est précisément définie. Cette architecture système inclut les différentes vues (opérationnelle, fonctionnelle et technique) et les différents points de vue (conception, supervision, opération, maintenance) du système. Cette architecture système est un élément incontournable de respect des contraintes de coût, de délai, de qualité et de performance inhérentes à un projet spatial. On commence également à sélectionner et définir, préliminairement, des solutions techniques.
- La définition détaillée n'a lieu que lors de la phase C.
- La phase D correspond à la phase de réalisation et de test des produits.
- C'est seulement lors de la phase E que le système va entrer dans sa période d'utilisation. Une fois lancé, une dernière qualification en vol a lieu puis l'exploitation peut commencer.
- Lorsque sa mission est terminée, le système entre en phase F, qui correspond à la fin de vie du satellite.
Cycle en V
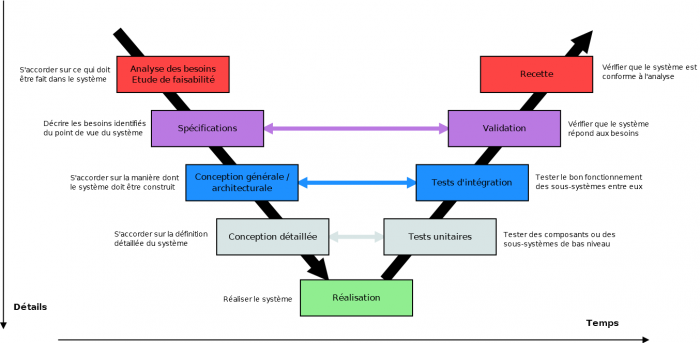
Cycle en V d'un produit. Chaque étape de conception correspond à une étape de validation, de la même couleur.
Crédit :
Gary Quinsac
Phases d'un projet spatial
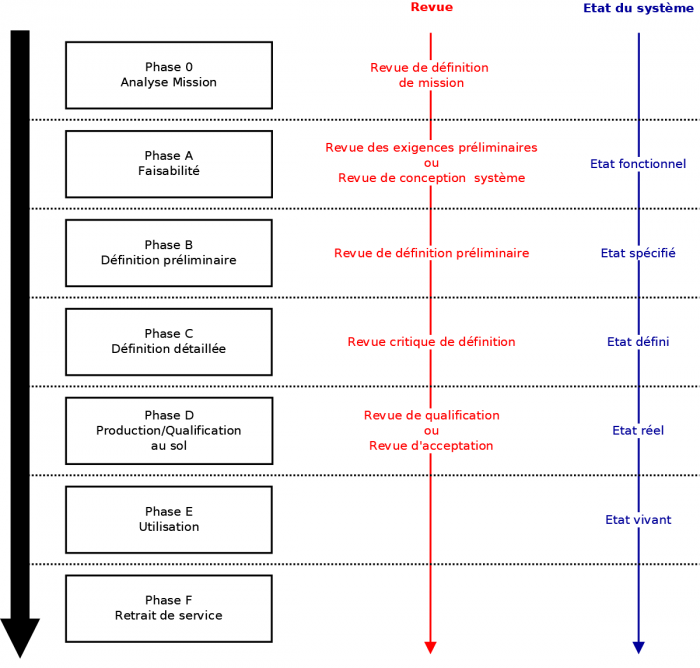
Phases d'un projet spatial. Chaque phase correspond à un état d'avancement du système et se conclut par une revue de projet.
Crédit :
Gary Quinsac
Nanosatellites
Auteur: Gary Quinsac
Standard CubeSat
Le standard CubeSat a été défini en 1999 par l'Université polytechnique de Californie (Cal Poly) et l'Université de Stanford comme un format de nanosatellites. Ce standard définit une unité de base, appelée "U", qui est un cube de 10 cm d’arête pour une masse d'environ 1,3 kg. Ces unités peuvent être assemblées de manière à obtenir des satellites plus volumineux, appelés "2U", "3U", "6U", "12U" ou même "27U" en fonction du nombre d'unités utilisé. Outre son format réduit, ce standard permet une importante réduction des coûts financiers et opérationnels :
- Possibilité pour un CubeSat d'être lancé en tant que charge utile secondaire, à condition qu'il n'amène pas de risque supplémentaire à la mission principale. L'extérieur de la structure des CubeSat étant standardisé, cela permet l'utilisation de "déployeurs" qui assurent l'interface entre le satellite et le lanceur. Le CubeSat est placé en position éteinte dans un déployeur fermé (P-POD ou équivalent) attaché à la fusée qui assure le lancement. Le CubeSat reste ainsi dans le déployeur jusqu’à son largage dans l’espace par ouverture du déployeur. Le largage déclenche la mise sous tension du CubeSat et donc le début de sa mission ;
- Fabrication en série donnant lieu à l'apparition de composants sur étagère (COTS pour "Components On The Shelf" en anglais) ;
Illustration du standard CubeSat
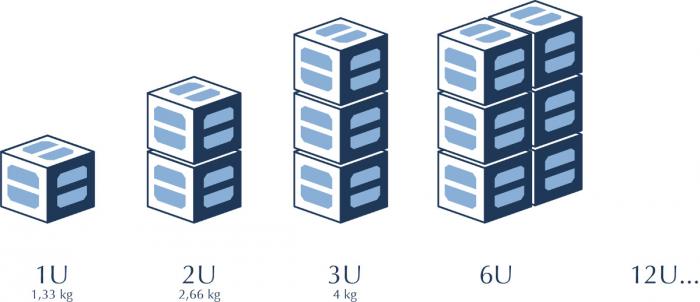
Chaque unité ("U) est un cube de 10 cm d’arête pour une masse d'environ 1,3 kg. Il est possible d'assembler plusieurs unités.
Crédit :
C²ERES, Campus et Centre spatial de PSL
Applications pour les CubeSats
Adopté dans différents secteurs
Il est possible de classer les CubeSats en différents secteurs et par extension tous les satellites de moins de 50 kg (échelles "nano" et en partie "micro"), dont les CubeSats forment la majeure partie :
- Secteur civil : ils sont utilisés pour des activités non militaires et à but non lucratif. On peut distinguer les deux catégories suivantes :
- Secteur académique : secteur historique des CubeSats, il regroupe l'ensemble des satellites développés à des fins pédagogiques. L’objectif principal est de former les étudiants à un certain nombre de disciplines d’ingénierie nécessaires pour réaliser un satellite. C’est dans ce but que des universités américaines ont créé le standard CubeSat. La mission particulière du satellite n’est donc pas en soi l’objectif prioritaire.
- Secteur public : on y retrouve tous les CubeSats des agences nationales ou des laboratoires de recherche (exemple : NASA).
- Secteur militaire : ce secteur regroupe les opérateurs dont l'objectif principal est de participer à des activités de défense nationale (exemple : US Naval Research Laboratory). La demande des opérateurs militaires devrait être constante dans les années à venir.
- Secteur commercial : les opérateurs de cette catégorie envoient des satellites pour générer de l'activité et du profit (exemple : Spire). Ce secteur commercial devient le principal moteur du lancement de nouveaux CubeSats, avec plus de 70 % des lancements prévus dans les 5 prochaines années.
De nombreuses applications
Le même classement peut être fait concernant les familles d'applications :
- CubeSat technologique : l’objectif principal est de démontrer une technologie particulière en environnement spatial avec un satellite beaucoup moins cher qu’une mission traditionnelle. Ainsi les nanosatellites peuvent nous aider à préparer les instruments de demain. Si la mission du nanosat est un succès, la technologie aura un niveau de maturité technologique (TRL pour "technology readiness level" en anglais) plus élevé, ce qui permettra de la proposer plus tard pour une mission spatiale scientifique encore plus ambitieuse et pas nécessairement au format nanosatellite.
- CubeSat scientifique : le CubeSat peut aussi embarquer un instrument de mesure. L’objectif principal est alors de réaliser cette mesure scientifique. Les applications scientifiques émergent peu à peu, avec une diversification de concepts, comme le CubeSat d’accompagnement d’une mission mère qui peut aller reconnaître le terrain avant de s’approcher d’un astéroïde ou comme les flottilles ou les essaims de nanosatellites pour des mesures "coopératives" (mesures simultanées par plusieurs CubeSats).
- CubeSat d'observation de la Terre / de télédétection : le satellite se concentre sur l'étude de la Terre et son atmosphère. La plupart des CubeSats commerciaux se concentre sur ce type d'applications (Planet Labs et Spire).
- CubeSat de communication : le CubeSat relaie des signaux émis par des stations émettrices vers des stations réceptrices. On retrouve de nombreux CubeSats pédagogiques dans cette catégorie (ITF 2, lancé le 12/2016).
Une tendance à l'embonpoint
Depuis la création de ce standard, le nombre de lancements a fortement augmenté au fil des ans. Cette tendance ne fait que se confirmer avec les nombreux nouveaux acteurs du marché, qu'ils se placent du côté de la conception de CubeSats ou de leur lancement. Il est intéressant de noter que si les CubeSats de petit format (1U, 2U et 3U) ont été privilégiés jusqu'à présent, des formats 12U et 27U sont maintenant envisagés afin d'offrir des profils de mission plus flexibles (missions interplanétaires, plus grosse charge utile) tout en préservant les avantages offerts par la standardisation, faisant varier le profil des CubeSats envoyés.
Nano/microsatellites par secteur (1 - 50 kg)
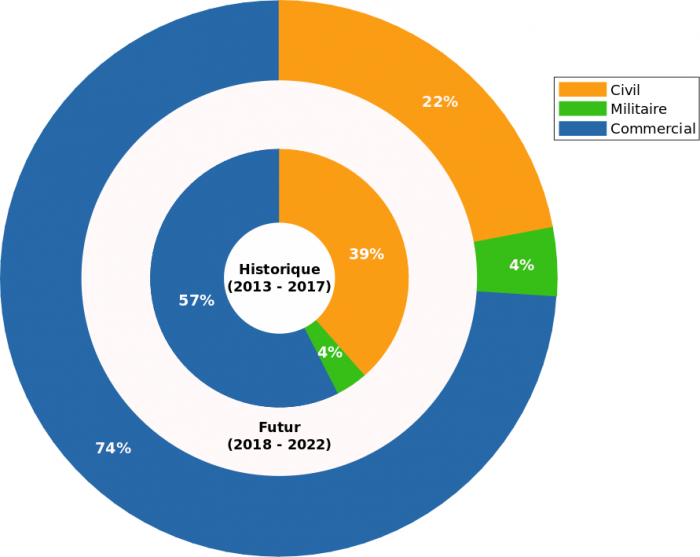
Le secteur commercial est en très forte augmentation, devenant bientôt le secteur dominant les satellites de 1 à 50 kg.
Crédit :
Gary Quinsac / Données de SpaceWorks - Nano/Microsatellite Market Forecast, 2018
Nano/microsatellites par application (1 - 50 kg)
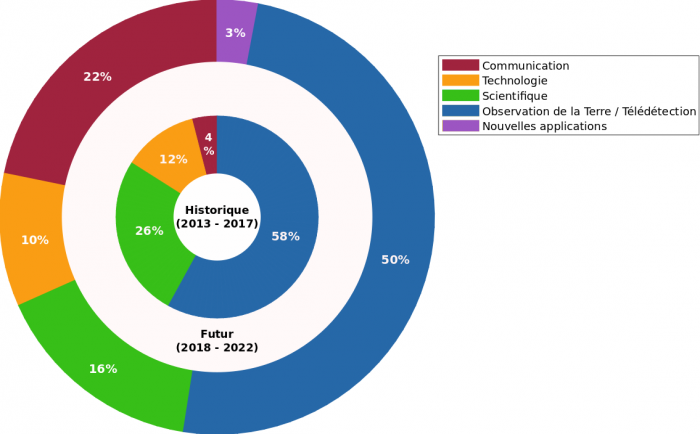
Le format de ces satellites est particulèrement intéressant pour la réalisation de constellations d'observation de la Terre. Les progrès réalisés sur la miniaturisation et les retours d'expérience des premières missions poussent les acteurs à considérer sérieusement leur utilisation dans un but scientifique.
Crédit :
Gary Quinsac / Données de SpaceWorks - Nano/Microsatellite Market Forecast, 2018
Lancements des nano/microsatellites
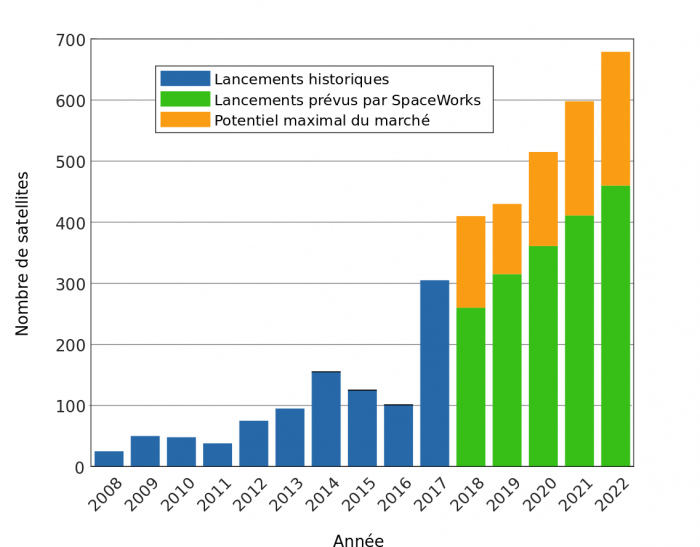
Après deux années de stagnation majoritairement due à des retards de lancement, l'année 2017 a vu une forte augmentation du nombre de lancements. Cela correspond à la croissance attendue pour ce marché, avec près de 2600 lancements attendus d'ici 5 ans.
Crédit :
Gary Quinsac / Données de SpaceWorks - Nano/Microsatellite Market Forecast, 2018
Evolution de la taille des nanosatellites
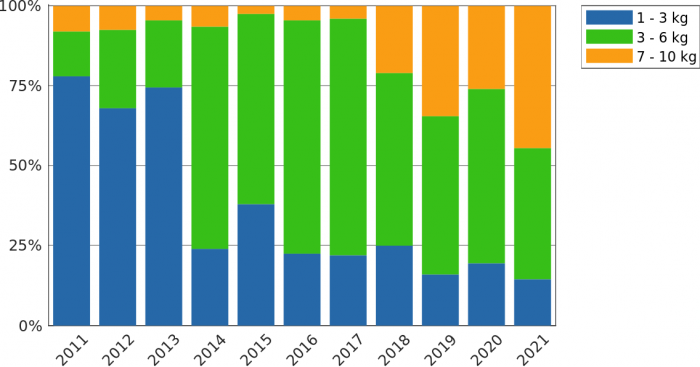
On constate une augmentation de la taille des nanosatellites afin de répondre aux demandes de charges utiles plus complexes. Néanmoins, le format 3U devrait rester le plus populaire dans les 5 années à venir.
Crédit :
Gary Quinsac / Données de SpaceWorks - Nano/Microsatellite Market Forecast, 2018
Sous-systèmes
Comme nous l'avons vu précédemment, un satellite se décompose en différents sous-systèmes essentiels à son bon fonctionnement :
- la charge utile,
- la structure porteuse,
- le contrôle thermique,
- la génération, le stockage et la distribution d'énergie,
- la télécommunication,
- la télémesure, la télécommande et la localisation,
- le traitement, le stockage et la gestion des données à bord,
- le contrôle d'attitude et d'orbite,
- la propulsion.
Charge utile
La charge utile est le sous-système qui réalise les fonctions correspondant à l'objectif de la mission. Si celle-ci varie fortement d'une mission à l'autre, les éléments suivants qui forment la plate-forme sont généralement présents sur tous les satellites.
Structure porteuse
La structure porteuse a pour but d'assurer l'interface avec le lanceur, la cohésion mécanique du satellite et le support des équipements. Elle est aussi appelée "architecture mécanique". L'intégrité du satellite doit être assurée dans les différents environnements qu'il rencontrera au cours de sa vie, c'est-à-dire le sol, le lancement et l'orbite.
- Au sol, il est victime de sollicitations mécaniques de type quasi-statique lors de la phase d'intégration et l'ensemble de ses composants est soumis à la gravité (1 g au sol), qui peut entraîner des déformations par différence avec l'environnement orbital. Le transport et la manutention peuvent être sources de chocs et de conditions climatiques variables (- 40°C, + 40°C). Les longues périodes de stockage nécessitent un contrôle de l'environnement (pression, température, hygrométrie) afin de ne pas dégrader les caractéristiques des éléments structuraux. A cela s'ajoutent les essais mécaniques qui constituent la source principale de sollicitation mécanique au sol.
- Durant le lancement, différents éléments sont dimensionnants du point de vue mécanique. On peut citer l'allumage des moteurs et le décollage, la pression dynamique et le passage du mur du son, la séparation des propulseurs latéraux à poudre (EAP) ou encore la séparation de la coiffe. Ils sont définis dans les Manuels Utilisateurs des Lanceurs par l'accélération statique continue, les vibrations à basse fréquence, l'environnement acoustique et les chocs dus aux séparations pyrotechniques.
- Lors de sa vie orbitale, le satellite est soumis à un cyclage en température dû aux variations de l'environnement thermique externe et à la dissipation des électroniques internes, générant des gradients thermiques sur la structure. L'utilisation de matériaux organiques, quant à elle, pose des problèmes hygro-élastiques. Une fois dans l'espace (ou même dans la coiffe du lanceur), ces matériaux subissent une déformation liée à la désorption de l'humidité préalablement absorbée au sol. Dernier aspect à ne pas négliger, les vibrations en orbite provoquées par les parties mobiles de certains équipements (roues, gyroscopes, mécanismes d'orientation des générateurs solaires...) peuvent altérer l'alignement d'optiques particulièrement sensibles.
Contrôle thermique
Le contrôle thermique a pour fonction de maintenir les équipements dans leur plage de température de fonctionnement, quelle que soit la phase de la mission, et ce durant toute la durée de vie du satellite. Dans le cas de missions nécessitant une grande précision astrométrique, le contrôle thermique permet également d'uniformiser les températures afin d'assurer une stabilité dimensionnelle (et ainsi éviter des phénomènes de dilatation/contraction par exemple). Pour ce faire, on peut faciliter ou interdire certains échanges thermiques de façon passive, ou utiliser des actionneurs (des réchauffeurs pour réchauffer ou des radiateurs pour refroidir) pour réguler la température. Ce contrôle thermique s'effectue dans des conditions très particulières, celles du milieu spatial, qui limitent le nombre d'acteurs. Nous pouvons classer les acteurs en deux catégories : les sources froides et les sources chaudes.
- Le Soleil, qui génère au voisinage de la Terre un flux de 1500W/m2, est l'une des sources chaudes. Son flux décroît en 1/D2, D étant la distance au Soleil. Pour une sonde spatiale s'éloignant fortement du Soleil, l'impact du flux solaire décroîtra donc rapidement.
- Les planètes, telles que la Terre, sont elles aussi des sources chaudes. Elles réfléchissent le flux solaire, c'est ce que l'on appelle le flux albédo. Elles émettent également directement un rayonnement.
- Les surfaces externes du satellite se refroidissent en émettant un rayonnement vers le fond du ciel (partie du ciel sans le Soleil et les planètes) qui n'est pas réfléchi vers le satellite. Néanmoins, l'espace est à l'origine d'un rayonnement dont le spectre correspond à un corps noir à 3 K. Ce rayonnement, appelé fond diffus cosmologique, est le vestige d'une phase importante de notre univers : sa réionisation 380 000 ans après le Big Bang. Cela veut dire que le fond du ciel consitue un puits radiatif infini et qu'un corps inerte dans l'espace tend vers une température d'équilibre de 3 K.
 Complément : modes de transfert d'énergie
Complément : modes de transfert d'énergie
Il existe trois modes de transfert d'énergie :
- Le transfert par conduction est l'échange d'énergie, sous l'effet d'une différence de température, entre deux corps en contact physique ou au sein d'un même corps solide.
- La convection thermique désigne l'échange d'énergie à l'interface d'un fluide en mouvement sous l'effet d'une différence de température. L'absence de fluide conducteur (air) dans l'espace empêche ce type de transfert thermique vers l'extérieur du satellite.
- Le transfert radiatif (ou transfert par rayonnement) représente l'unique transfert possible avec l'espace. Il représente le transfert d'énergie par radiation et implique l'interaction du rayonnement avec la matière.
Génération d'énergie
La génération d'énergie permet le fonctionnement de l'engin spatial en lui fournissant l'énergie électrique dont il a besoin. En effet, ce dernier étant mobile et autonome, il a besoin de produire son électricité. Le système d'alimentation électrique est découpé en quatre éléments qui sont la production (ou source primaire), le stockage (ou source secondaire), la régulation et la distribution.
- La production électrique utilise généralement le flux solaire grâce à des générateurs solaires placés sur la structure du satellite. Ces générateurs solaires, aussi appelés panneaux solaires, peuvent être déployables afin d'offrir une grande surface d'accumulation malgré un volume restreint dans la coiffe du lanceur. Des cellules solaires assurent la conversion de l'énergie lumineuse en énergie électrique, avec un certain rendement. Outre l'énergie solaire, des missions lointaines pilotées par les agences américaine ou russe ont également utilisé des générateurs nucléaires ou isotopiques (sonde Cassini-Huygens).
- L'énergie produite est ensuite stockée dans les batteries électrochimiques afin d'alimenter le satellite lors de phases d'éclipse ou de consommation instantanée supérieure à la production des générateurs.
- La régulation et la distribution permettent de fournir à la charge utile et aux autres éléments nécessitant de l'énergie une alimentation présentant des caractéristiques électriques précises et compatibles avec les différents équipements. La régulation permet également de garantir la durée de vie de la batterie. Pour ce faire, on limite la profondeur de décharge, c'est-à-dire la quantité d'énergie fournie par la batterie, on limite le courant de charge et de décharge...
Ce sous-système occupe usuellement entre 20 % et 30 % de la masse sèche (réservoirs vides d'ergols) d'un satellite classique.
Télécommunication
Le sous-système de télécommunication utilise des émetteurs, des récepteurs ou des transpondeurs afin de gérer l'ensemble des fonctions de communication. S'il s'agit d'un satellite de communication, ce sous-système peut alors devenir la charge utile du satellite.
Télémesure, télécommande et localisation
Les équipements de télémesure, télécommande et localisation constituent un ensemble de télécommunications de servitude transmettant au sol les télémesures de différents paramètres soumis à contrôle (température d'un équipement, charge d'une batterie) et recevant les télécommandes pour les équipements à opérer (plate-forme et charge utile).
Chaîne de traitement, de stockage et de gestion bord
Les informations transitant dans le satellite sont prises en charge par la chaîne de traitement, de stockage et de gestion bord. Ce sous-système s'assure de la bonne distribution des données vers les équipements. Il est également en charge du stockage des données avant que celles-ci soient transmises, généralement à une station sol.
Système de contrôle d'attitude et d'orbite
Le système de contrôle d'attitude et d'orbite (SCAO) assure deux types de mouvement : celui autour de son centre de gravité (attitude) et celui de son centre de gravité (orbite). En d'autres termes, il est responsable de l'orientation et de la position du satellite dans l'espace. En fonction de l'attitude recherchée, les commandes d'attitude impriment les corrections d'orientation autour du centre de gravité. Le maintien du satellite sur l'orbite prévue est indispensable à la plupart des missions. Le sous-système de propulsion crée les incréments de vitesse nécessités par les manœuvres d'orbite. Celles-ci sont commandées depuis le sol, ou déterminées à bord, la détermination d'orbite à bord étant aujourd'hui rendue possible par les navigateurs embarqués qui permettent d'accroître l'autonomie des satellites.
Propulsion
La propulsion, enfin, fonctionne de pair avec le SCAO. Elle est un actionneur du SCAO, assez complexe pour être traité séparément, qui a pour fonction de créer les variations de vitesse nécessaires aux manœuvres du satellite.
 Aller plus loin
Aller plus loin
Schéma éclaté du CubeSat ArduSat3
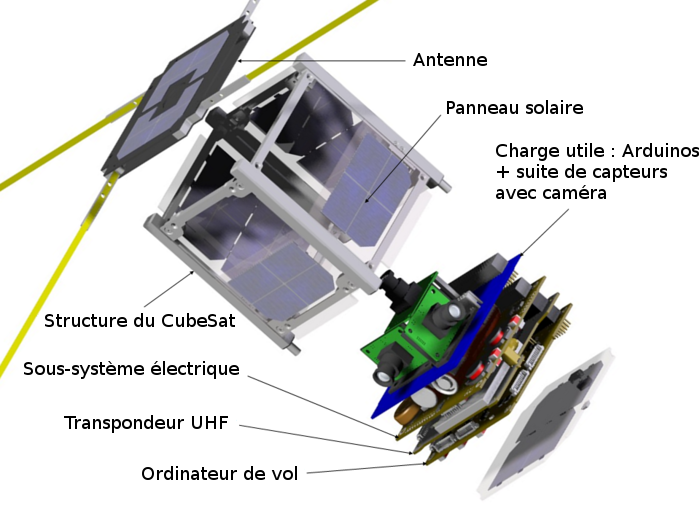
On retrouve une partie des sous-systèmes classiques d'un satellite sur ce CubeSat 1U. On remarque également qu'ils se présentent généralement sous la forme de cartes disposées les unes après les autres dans la structure du CubeSat.
Crédit :
Wikipedia
Exemples de missions CubeSats
GOMX-3 un satellite de démonstration téchnologique
GOMX-3 est une collaboration entre l'ESA et GOMspace (Danemark) embarquant différentes charges utiles de démonstration technologique :
- un contrôle d'attitude 3 axes avec 1 degré de précision, permettant jusqu'à 7 changements d'attitude par orbite et un suivi de cible,
- un récepteur expérimental pour détecter les signaux ADS-B (Automatic Dependent Surveillance-Broadcast) diffusés par les avions en vol,
- une radio réalisée par logiciels pour évaluer les faisceaux de réception des satellites de télécommunication,
- un émetteur bande-X développé par Syrlinks pour télécharger des données à haut débit.
 Focus sur l'émetteur bande-X
Focus sur l'émetteur bande-X
De nombreux types de missions sont maintenant rendus possibles par la miniaturisation des charges utiles, qu'elles soient scientifiques ou technologiques. L'une des principales limitations de ces missions en orbite basse est le volume de données pouvant être téléchargées par orbite. Actuellement, les CubeSats embarquent des sous-systèmes de télémétrie UHF et bande-S qui permettent de télécharger jusqu'à quelques centaines de mégaoctets (Mo) par jour. Ce volume de données est limité par la durée de visibilité entre la station sol et l'antenne du satellite ainsi que le débit (~100 ko/s en UHF et ~1Mo/s en bande-S). Afin d'augmenter les taux de transmission tout en restant compatible avec les stations sol existantes, le CNES et l'ESA ont voulu tester un émetteur-récepteur en bande-S et un émetteur en bande-X, tous deux miniaturisés pour le format CubeSat. L'émetteur en bande-X permet des débits de l'ordre de plusieurs Go par survol d'une station sol compatible bande-X (entre 3,4 et 5 m dans ce cas), tout en étant adapté aux dimensions d'un CubeSat-3U (< 10 W et 300 g pour le sous-système).
Après une année d'opération, le satellite a effectué sa ré-entrée atmosphérique. Tous les objectifs ont été atteints et la mission nominale a même été dépassée, permettant de démontrer d'autres capacités.
QB50 une flotte de CubeSats scientifiques universitaires
L'objectif de la mission QB50 est de démontrer la possibilité de lancer un réseau de satellites construits par des équipes universitaires à travers le monde pour effectuer une étude scientifique de la basse thermosphère. De nombreux enjeux du standard CubeSat se retrouvent à travers les différents objectifs de cette mission :
- faciliter l'accès à l'espace pour des missions spatiales à petite échelle,
- étudier la couche la moins explorée de l'atmosphère (entre 200 et 380 km),
- effectuer des démonstrations technologiques avec certains CubeSats, notamment QARMAN (étude de la rentrée atmosphérique) et InflateSail (test d'une voile solaire),
- permettre à des étudiants en ingénierie de concevoir et construire ces satellites.
 Focus sur l'étude scientifique de la thermosphère
Focus sur l'étude scientifique de la thermosphère
La majeure partie des CubeSats de QB50 a comme objectif scientifique d'effectuer des mesures in-situ en de nombreux points de la thermosphère. Par le passé, cette région a été étudiée par des satellites aux orbites très elliptiques (périgée à 200 km et apogée à 3000 km), ne permettant de passer que quelques dizaines de minutes dans la zone d'étude. Les différentes techniques actuelles sont limitées. Les fusée-sondes ("sounding rockets") permettent d'obtenir des mesures durant quelques minutes et le long d'une unique colonne. Des mesures à distance sont faites depuis le sol et des orbites plus élevées, typiquement entre 600 et 800 km. L'environnement est sondé grâce à la diffusion d'un signal de référence. De telles mesures sont rendues difficiles par la raréfaction de l'atmosphère dans la basse thermosphère qui empêche d'obtenir des signaux de retour de qualité. Le moindre coût des CubeSats permet d'accepter la très courte durée de vie inhérente à une orbite très basse, offrant une étude in-situ d'une période de plusieurs mois. Trois types d'instruments sont répartis parmi les satellites (un type par CubeSat), offrant ainsi une étude poussée des différents paramètres régissant le comportement de cette région de l'espace.
Autres missions
De nombreux projets de CubeSats sont développés dans le cadre de C2ERES (Campus et Centre de Recherche pour l’Exploration Spatiale), le pôle spatial de l'Université de Recherche PSL conjointement piloté par le LabEx ESEP et le Master OSAE. En août 2017, on en dénombre pas moins de 8, à des stades de développement différents :
- PICSAT, surveillance de l'exoplanète Beta Pictoris b
- METEORIX, spectre UV des météores pour analyser la composition des météoroïdes
- SERB, précurseur pour la surveillance de la variabilité solaire
- GPU4SPACE, qualification spatiale d'un GPU
- NANOPOT, Tests pour la maîtrise du potentiel électrique d'un nanosatellite
- OGMS-SA, un instrument d'astrochimie spatiale
- BIRDY-T, développement technologique pour la navigation autonome
- CIRCUS, étude de l'ionosphère avec STAR, une technologie nouvelle
 Aller plus loin
Aller plus loin
GomX-3
Illustration du CubeSat GomX-3 (3U) développé par GOMspace.
Crédit :
GomSpace
Lancements des CubeSats du programme QB50

En août 2017, 36 CubeSats du programme QB50 ont été lancés : 28 depuis la station spatiale internationale et 8 par le lanceur indien PSLV.
Crédit :
QB50
Système de Contrôle d'Attitude et d'Orbite
Auteur: Gary Quinsac
Introduction au Système de Contrôle d'Attitude et d'Orbite
Le contrôle d'attitude et d'orbite concerne tous les aspects nécessaires à la maîtrise de l'orientation et de la trajectoire du satellite. Il comprend :
- la prise en compte des phénomènes physiques gouvernant le déplacement du satellite;
- les méthodes pour mesurer l'état du satellite;
- la détermination des lois de contrôle et leur implémentation;
- les technologies nécessaires afin de produire ces actions de contrôle.
L'ensemble s'appelle le système de contrôle d'attitude et d'orbite (SCAO). Il se compose de différents éléments :
- les capteurs ou détecteurs, permettant de restituer les vitesses et positions angulaires définissant l'attitude,
- l'électronique et l'informatique de bord, chargées du traitement des informations provenant des capteurs,
- les actionneurs, permettant de maintenir une attitude, changer de pointage ou encore modifier les vitesses angulaires,
Le SCAO est l'un des sous-systèmes essentiels de la plupart des satellites. L'une de ses raisons d'être est l'existence de perturbations agissant sur un satellite via des couples ou forces extrêmement faibles qu'il faut utiliser ou compenser. Si rien n'entrave ces phénomènes, les conséquences de ces effets deviennent rapidement significatives. Ces perturbations peuvent être externes (c'est-à-dire causées par des phénomènes extérieurs au satellite) ou internes (c'est-à-dire liées à des mécanismes ou déplacements propres au satellite).
Au sein du SCAO, on a pour habitude de distinguer le contrôle d'attitude du contrôle d'orbite de la manière suivante :
- le Système de Contrôle de l'Attitude (SCA), qui concerne la maîtrise de l'attitude, c'est-à-dire l'orientation du satellite ou de son mouvement autour du centre d'inertie,
- le système de Guidage, Navigation et Contrôle (GNC) est lui en charge de la trajectoire du centre d'inertie du satellite et donc des paramètres orbitaux du véhicule spatial.
Dans la suite de ce cours nous insisterons sur le SCA, même si nous reviendrons par moments sur le système GNC. Il faut bien comprendre que les deux sont généralement développés de manière indépendante et gérés de façon autonome. Le SCAO dans son ensemble est en interaction avec les autres éléments du satellite. Ces interactions sont à l'origine de nombreuses contraintes essentielles lors du développement du SCAO.
 Définitions
Définitions
Quelques définitions sont importantes à ce stade.
- Détermination d'attitude : connaissance de l'orientation du satellite par rapport à un référentiel
- Contrôle d'attitude : processus permettant d'atteindre et de maintenir l'orientation ou le taux de changement d'orientation désiré
- Navigation : connaissance de la position et de la vitesse du satellite par rapport à un référentiel
- Contrôle d'orbite : processus permettant d'atteindre et de maintenir l'orbite désirée
- Guidage : séquence de commande depuis l'état (attitude ou position orbitale) actuel à un état désiré
Digramme en bloc d'un SCAO
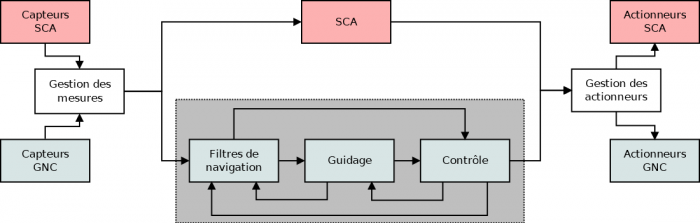
Diagramme en bloc d'un système de contrôle d'attitude et d'orbite.
Crédit :
Gary Quinsac
Relations fonctionnelles du SCAO
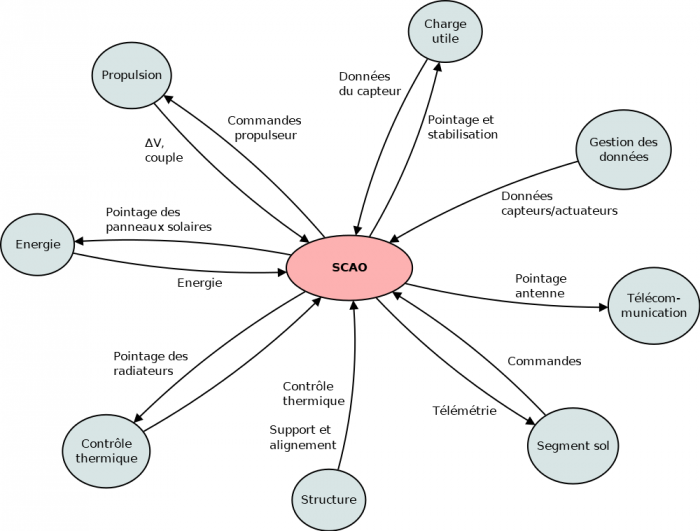
Schéma des relations fonctionnelles entre le système de contrôle d'attitude et d'orbite et les autres sous-systèmes du satellite.
Crédit :
Gary Quinsac
Système de Contrôle d'Attitude
Le sous-système en charge de l'attitude du satellite se nomme le système de détermination et de contrôle d'attitude (SCA). Il a différents rôles en fonction des modes du satellite. Il doit :
- fournir un contrôle du spin et un pointage pour la charge utile, l'énergie, la communication et les systèmes de régulation thermique dans les modes nominal et de survie,
- fournir un contrôle de l'attitude et de son taux de variation pour le transfert orbital et le maintien à poste,
- fournir une connaissance de l'attitude suffisamment précise pour mener à bien les objectifs de la mission.
La détermination et le contrôle d'attitude nécessitent plusieurs outils qui seront développés dans la suite du cours.
Représentation d'attitude
L'attitude du satellite est exprimée par l'orientation de son repère par rapport à un référentiel standard (inertiel, orbital, fixé par rapport à un objet...), comme détaillé dans le chapitre sur la représentation d'attitude. Plusieurs outils existent, de la matrice du cosinus directeur aux quaternions, en passant par les angles d'Euler.
Détermination d'attitude
La détermination ou estimation d'attitude fait le liant entre les mesures fournies par les différents capteurs présents à bord du satellite et la connaissance de l'attitude. La détermination d'attitude nécessite au moins deux mesures de directions bien séparées. Il faut ici différencier les techniques de détermination directe d'attitude des techniques d'estimation :
- les approches directes calculent la matrice de transformation directement à partir des vecteurs de mesure,
- les techniques d'estimation nécessitent une connaissance initiale grossière de l'attitude et une estimation des sources d'erreur de mesure. Les techniques d'estimation peuvent incorporer plusieurs types de capteurs, prendre en compte des statistiques d'erreur et sont généralement plus précises que les méthodes dites "directes".
Contrôle d'attitude
Le contrôle d'attitude rentre dans le domaine de la théorie du contrôle. Des lois de contrôle doivent être implémentées afin d'amener le système d'un état initial donné à un état final souhaité, tout en respectant certains temps de réponse. Les asservissements mis en oeuvre doivent être les moins sensibles possible vis-à-vis des perturbations, qu'elles soient internes ou externes. Des actionneurs sont enfin chargés d'appliquer les corrections d'attitude ainsi déterminées.
Une distinction importante doit être effectuée entre les contrôles d'attitude passif et actif.
- Le contrôle d'attitude passif se base sur l'utilisation des propriétés physiques du satellite et de son environnement pour contrôler l'attitude du véhicule. Cette technique exige un matériel moins complexe et généralement moins coûteux. Nous ne rentrerons pas dans le détail de ces techniques, mais l'on peut tout de même citer le contrôle d'attitude par gradient de gravité
- le contrôle d'attitude actif, en revanche, est plus sophistiqué. Il permet d'obtenir des performances supérieures, c'est-à-dire des pointages beaucoup plus précis et des manœuvres plus rapides.
Boucle SCA
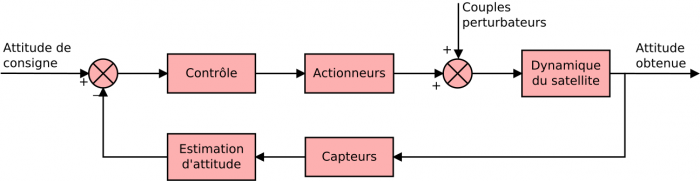
Boucle de contrôle d'attitude.
Crédit :
Gary Quinsac
Système de Guidage, Navigation et Contrôle
Lorsque l'on s'intéresse à l'orbite du satellite, on parle alors de guidage, navigation et contrôle (GNC). C'est une branche de l'ingénierie consacrée à la conception des systèmes de contrôle des véhicules (automobiles, bateaux, avions et satellites). La navigation répond à la question "où sommes-nous ?", le guidage à la question "comment aller à notre destination ?" et le contrôle "quelle commande donner au véhicule ?". En somme, cela concerne la détermination d'orbite et la majeure partie du contrôle, à l'exception de la réalisation du contrôle qui est prise en charge par le sous-système de propulsion. Ce sous-système joue un rôle essentiel dans le succès des missions qui impliquent un rendez-vous, de l'arrimage ("docking") et des opérations de proximité. Le logiciel de GNC se compose d'un filtre de navigation, d'un algorithme de guidage et d'un algorithme de contrôle. Ce sous-système doit ainsi :
- fournir la position et la vitesse du satellite pour pointer les antennes et la charge utile,
- fournir l'instant, la magnitude, la durée et la direction des poussées pour effectuer un transfert orbital et un maintien à poste,
- fournir la position des autres corps pour piloter les éléments mobiles du satellite.
Il ne faut pas confondre le système GNC embarqué avec le système de dynamique de vol qui fait partie du segment sol. Le GNC doit faire face à des contraintes temporelles et de calcul beaucoup plus fortes, ce qui conduit généralement à des performances des logiciels en vol insuffisantes. Un suivi depuis le sol peut se faire a posteriori et ainsi fournir une mise à jour de paramètres tels que la trajectoire de référence. Les exigences du système GNC dépendent fortement du niveau d'autonomie attendu. L'autonomie à bord permet au segment spatial de continuer les opérations de mission et de survivre à des situations critiques sans avoir recours au segment sol. Plus l'autonomie est importante plus les coûts de développement sont importants, mais les coûts d'opération diminuent. De même, dans le cas de missions interplanétaires, la rareté des canaux de communication peut être une motivation pour limiter les interactions avec le segment sol. Rares ont été les satellites autonomes sur ce plan, même si nous pouvons citer SMART-1 de l'ESA et Deep Space 1 de la NASA. Dans la plupart des cas, une majeure partie des étapes nécessaires au contrôle d'orbite sont effectuées par le segment sol avant que des télécommandes soient transmises au satellite.
Navigation
À la manière de l'estimation d'attitude, l'objectif est d'obtenir une estimation de la position orbitale satisfaisant les exigences de la mission. La navigation est généralement implémentée sous la forme d'un filtre numérique joué par l'ordinateur de bord.
Guidage
Le guidage se sert de l'estimation fournie par la navigation et de la consigne mission pour calculer certains des points suivants :
- les manœuvres pour atteindre l'objectif, qu'elles soient impulsionnelles (ΔV en sortie de la fonction) ou continues (profil de poussée en sortie de la fonction),
- la trajectoire de référence (position et vitesse) pour une période future,
- les éphémérides nécessaires au bon fonctionnement d'autres sous-systèmes, basées sur la nouvelle trajectoire.
La trajectoire de référence est calculée par le segment sol et peut être mise à jour durant la mission. Les écarts à cette référence doivent rester suffisamment faibles afin que le guidage puisse les compenser au moyen de faibles variations du profil de poussée. Ces écarts peuvent être dus à des perturbations extérieures, des erreurs d'exécution de manœuvre, des incertitudes de navigation ou des délais opérationnels.
Contrôle
En s'appuyant sur l'estimation de l'état du véhicule (position, vitesse) fournie par le filtre de navigation et sur la trajectoire de référence calculée par la fonction de guidage, la fonction de contrôle s'assure de la bonne exécution de la manœuvre et corrige les erreurs résiduelles. La fonction de contrôle traduit donc les manœuvres reçues en entrée dans le format exigé par la fonction qui s'occupe de la gestion des actionneurs.
Dans le cas de propulseurs, le contrôle établit des forces dans le référentiel du satellite qui seront obtenues en contrôlant le niveau de poussée durant une durée déterminée ou en contrôlant la durée d'une poussée de puissance constante. Une fonction de gestion de la propulsion se chargera de sélectionner le propulseur optimal pour fournir la force ainsi que de fournir les couples réclamés par la fonction de contrôle de l'attitude du satellite.
Digramme en bloc d'un SCAO
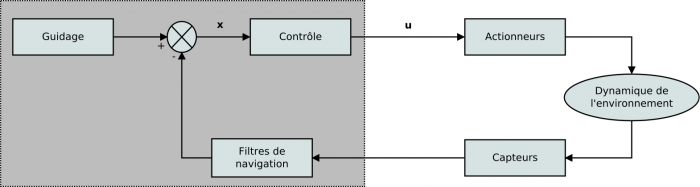
Boucle de contrôle d'un système GNC.
Crédit :
Gary Quinsac
Sonde SMART-1

Vue d'artiste de la sonde spatiale SMART-1 sur le chemin de la Lune. Elle était équipée d'un système de propulsion ionique et d'un système de GNC autonome.
Crédit :
ESA
Modes SCAO
Une fois séparé du lanceur, le satellite va parcourir une série de modes jusqu’à la fin de la mission. Des modes nominaux vont lui permettre de maintenir son attitude, atteindre son poste, déployer ses panneaux solaires et son antenne, le tout afin de se mettre en ordre de marche pour sa mission. Si nécessaire, ces modes d’opération peuvent être interrompus afin de réaliser son maintien à poste, la décharge du moment cinétique des roues à inertie ou répondre à un incident. Différents équipements sont utilisés en fonction de ces modes et certains sont cités en exemple dans la figure 1. On associe aux modes des exigences qui découlent des exigences mission, par exemple :
- Les exigences sur la détermination d'attitude dérivent de plusieurs exigences mission, notamment celle de décrire correctement la position d'une observation dans l'espace, ou peuvent découler d'une allocation d'une exigence de pointage de plus haut niveau (par exemple, afin de pointer un objet avec une certaine précision on a besoin de déterminer l'attitude avec telle précision).
- Parmi les exigences de pointage, on peut citer la définition de la cible et de ce qui doit la pointer (sous-système, instrument etc.). Les exigences peuvent ensuite être classées en 2 catégories : la précision et la stabilité de pointage.
- La précision de pointage est une partie du budget total de pointage de la charge utile, dans lequel se trouvent également des effets mécaniques, thermiques et de mesure.
- La stabilité de pointage découle habituellement des exigences de résolution des instruments. En effet, des mouvements à haute fréquence du satellite ont tendance à dégrader la résolution.
- L'agilité du satellite est souvent nécessaire à une mission pour passer d'un pointage à un autre en un certain temps. Ces exigences ont tendance à contraindre le choix des actionneurs et des méthodes de contrôle.
- La phase dite d'acquisition concerne les satellites équipés de panneaux solaires pour la génération d'énergie. Elle intervient au tout début de la mission, une fois que le satellite est séparé du lanceur, et consiste à stabiliser le satellite et à pointer ses panneaux solaires vers le Soleil avant que ses batteries ne se soient vidées. La connaissance précise du lanceur est essentielle afin de prendre en compte l'ensemble des conditions initiales possibles lors de la conception.
- Des exigences concernent églament la fiabilité et la survie. Il faut déterminer le niveau de fiabilité/redondance nécessaire pour récupérer d'anomalies, ce que le SCAO doit faire en réponse à une anomalie...
Modes SCAO
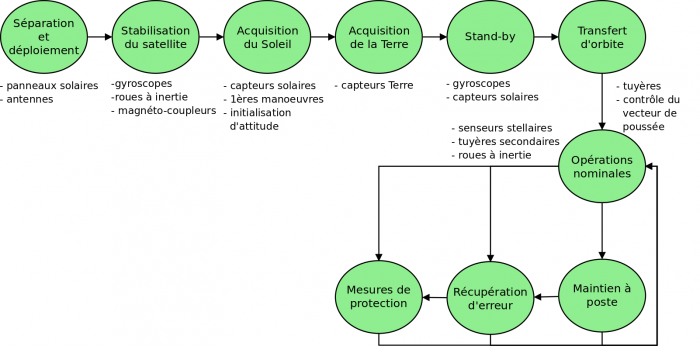
Modes SCAO typiques avec des exemples associés. Après une phase d'initialisation débutée par la séparation et le déploiement et conclue par le transfert d'orbite, le satellite entre dans un mode d'opérations nominales.
Crédit :
Gary Quinsac
Comprendre
Auteur: Gary Quinsac
Réferentiels et transformations
Auteur: Gary Quinsac
Systèmes de coordonnées
Auteur: Gary Quinsac
Généralités
Afin de déterminer la position et l'orientation d'un objet dans l'espace, on fait appel aux systèmes de coordonnées. Dans cette partie, il ne faudra pas confondre les notions de référentiel et système de coordonnées. Un système de coordonnées est notamment défini par son centre (on parle de référentiels géocentrique ou héliocentrique), son plan de référence (équatorial, écliptique) et ses axes. En ce qui concerne les systèmes de coordonnées, on a pour habitude d'utiliser les suivants :
- systèmes de coordonnées rectangulaires (ou cartésiennes), qui à un point de l'espace font correspondre trois distances sur chacun des axes du repère;
- systèmes de coordonnées cylindriques, qui décrivent la position d'un point à l'aide d'une distance au centre, d'un angle et d'une hauteur;
- systèmes de coordonnées sphériques, qui à un point de l'espace associent une distance au centre et deux angles. Ce type de système est couramment utilisé en géographie et en astronomie.
Système de coordonnées inertiel
Un référentiel inertiel (ou galiléen) est un référentiel dans lequel le principe d'inertie est vérifié. Tout corps libre est en mouvement de translation rectiligne uniforme ou au repos. Tout référentiel en mouvement de translation rectiligne et uniforme par rapport à un référentiel inertiel est lui-même inertiel. Les lois de la mécanique sont invariantes par changement de référentiel inertiel. On a l'habitude de distinguer un référentiel considéré comme fixe par rapport à un objet en rotation, comme le repère terrestre, avec un repère dont les axes sont fixés par rapport à une position absolue.
 Termes d'inertie
Termes d'inertie
Dans un référentiel non inertiel, par exemple animé d’un mouvement accéléré par rapport à un référentiel galiléen, il faut faire intervenir les termes d’inertie (comme détaillé par la suite). Ces termes se traduisent par des pseudo-forces, qui se distinguent des forces prises en compte dans un référentiel galiléen car elles ne sont pas associées à une interaction entre le corps dont on étudie le mouvement et un autre corps.
Systèmes de coordonnées célestes
En astronomie, on utilise habituellement les repères cylindriques et sphériques amputés de leur coordonnée de distance. Pour des raisons pratiques, on suppose souvent que les objets observés se situent à des positions fixes à l'intérieur de la sphère céleste, à condition que leur distance soit suffisante.
Un système de coordonnées céleste a pour fonction de déterminer une position dans le ciel. Il existe plusieurs systèmes, utilisant une grille de coordonnées projetée sur la sphère céleste, de manière analogue aux systèmes de coordonnées géographiques utilisés à la surface de la Terre. Les systèmes de coordonnées célestes diffèrent seulement dans le choix du plan de référence, qui divise le ciel en deux hémisphères le long d'un grand cercle (le plan de référence du système de coordonnées géographiques est l'équateur terrestre). Chaque système est nommé d'après son plan de référence.
Système de coordonnées horizontales
Coordonnées horizontales
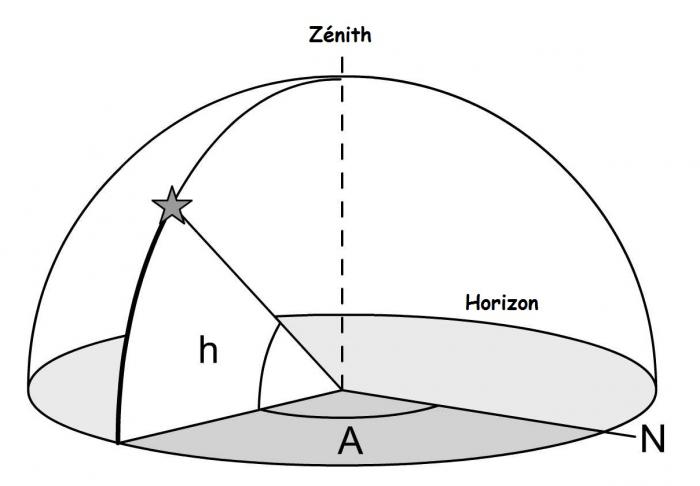
Les coordonnées horizontales locales sont la hauteur (h) et l'azimut (A). La hauteur varie de 0° (horizon) jusqu'à 90° (zénith) et l'azimut est mesuré sur le plan horizontal à partir du Nord (N). Un objet de hauteur négative n'est pas visible depuis le lieu d'observation.
Crédit :
Wikipedia
Le système de cordonnées horizontales, également appelé système local ou système de coordonnées alt-azimutales, est un système de coordonnées célestes utilisé en astronomie par un observateur au sol. Le système, centré sur l'observateur, sépare le ciel en deux hémisphères : l'un situé au-dessus de l'observateur et l'autre situé au-dessous, caché par le sol. Le cercle séparant les deux hémisphères, appelé horizon céleste, situe le plan horizontal. L'altitude (ou élévation, "h") et l'azimut (A), qui constituent les deux principales coordonnées de ce système, sont définis à partir de ce plan.
- L'altitude est l'angle entre l'objet et l'horizon local de l'observateur. Pour les objets visibles, cet angle est compris entre 0° (horizon) et 90° (zénith).
- L'azimut est l'angle de l'objet autour de l'horizon. C'est un cercle divisé en 360° établi sur le plan horizontal depuis le nord vers l'est (des exceptions à cette convention existent).
Ce système de coordonnées présente l'avantage d'être simple et local. Il est facile à établir à un endroit donné à partir du moment où l'observateur sait où se trouve l'un des points cardinaux. C'est la raison pour laquelle il est particulièrement utilisé par les télescopes au sol à monture azimutale, c'est à dire l'essentiel des télescopes les plus récents.
Système de coordonnées équatoriales
Coordonnées équatoriales projetées sur la sphère céleste
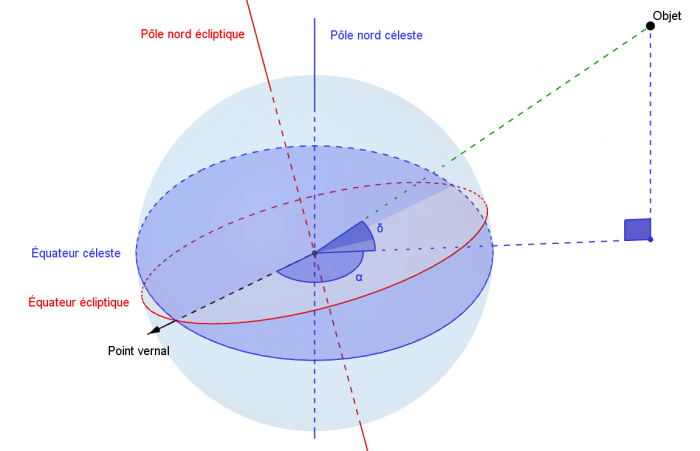
Un système équatorial est projeté sur la sphère céleste. Les longitude (α) et latitude (δ) d'un objet sont indiquées.
Crédit :
Gary Quinsac
Le système de coordonnées équatoriales est un système de coordonnées célestes dont les valeurs sont indépendantes de la position de l'observateur. Ceci est également vrai pour les systèmes de coordoonées écliptiques et galactiques. Ce système utilise comme plan de référence la projection de l'équateur de la Terre sur la sphère céleste. Cette projection s'appelle l'équateur céleste. Elle divise le ciel en deux hémisphères, chacun ayant comme axe de référence la projection d'un pôle terrestre, perpendiculaire à l'équateur céleste. À partir de ces divisions, le système permet d'établir deux coordonnées angulaires : l'ascension droite et la déclinaison.
- L'ascension droite (α) est l'angle mesuré sur l'équateur céleste à partir d'un axe pointant vers un point de référence, le point vernal, correspondant à l'intersection entre l'équateur céleste et l'écliptique. À partir de cet axe, l'angle est mesuré vers l'Est et comporte 24 divisions principales de 15° chacune, nommées « heures ». Chacune des heures se divise en minutes, et en secondes. Cette division de l'angle en heures, minutes et secondes permet de déterminer facilement combien de temps (en temps sidéral) il faudra à un astre pour atteindre un certain point dans le ciel.
- La déclinaison (δ) est l'angle mesuré perpendiculairement entre l'équateur céleste et l'objet céleste observé. Elle se mesure en degrés, positifs pour les objets situés dans l'hémisphère nord et négatifs pour ceux de l'hémisphère sud. La déclinaison varie ainsi de -90° (pôle sud) à +90° (pôle nord) en passant par 0° à l'équateur céleste. L'ascension droite et la déclinaison sont les équivalents astronomiques de la longitude et de la latitude.
Système de coordonnées écliptiques
Coordonnées écliptiques projetées sur la sphère céleste-
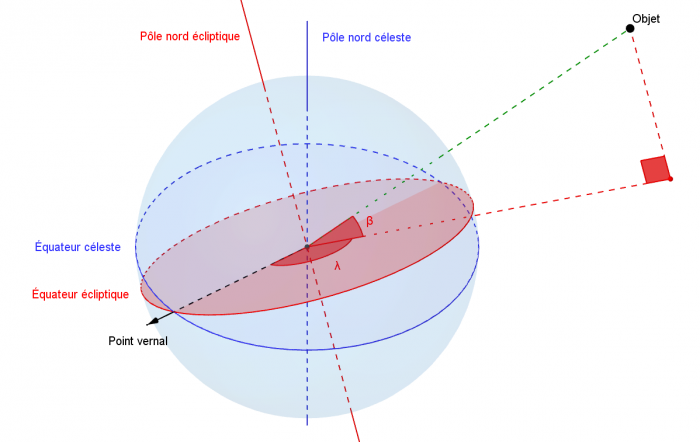
Un système écliptique est projeté sur la sphère céleste. Les longitude (λ) et latitude (β) d'un objet sont indiquées.
Crédit :
Gary Quinsac
Le système de coordonnées écliptiques est un système de coordonnées adapté aux objets célestes : il utilise le plan de l'écliptique (plan de l'orbite de la Terre autour du Soleil) comme plan de référence. Ce plan fait un angle d'approximativement 23° avec le plan équatorial terrestre, du fait de l'inclinaison de l'axe de rotation de la Terre. Ce repère est un système sphérique à deux dimensions.
- La longitude écliptique (λ) est l'angle entre le point vernal (le même que pour le système de coordonnées équatoriales), le centre du repère (le soleil) et la projection de l'objet sur ce plan. Cet angle se mesure en degrés.
- La latitude écliptique (β) représente l'angle entre le plan de l'écliptique, le centre du repère (le soleil) et l'objet.
Ce système peut être centré sur la Terre, le Soleil ou tout autre corps. Il est particulièrement utile pour les objets situés dans le système solaire.
Système de coordonnées galactiques
Coordonnées galactiques projetées sur la sphère céleste
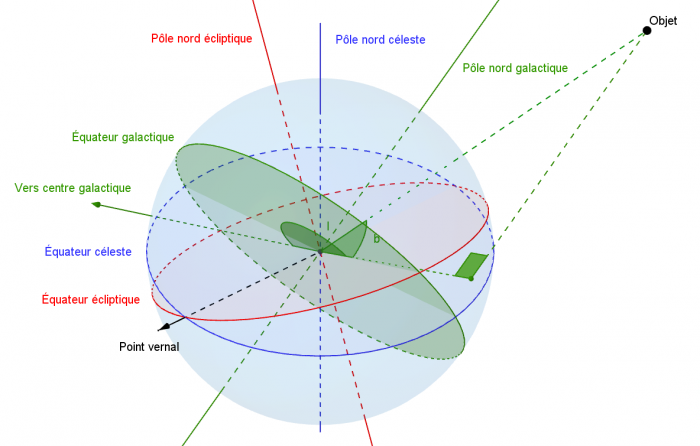
Un système galactique est projeté sur la sphère céleste. Les longitude (l) et latitude (b) d'un objet sont indiquées.
Les coordonnées galactiques sont adaptées aux objets situés dans notre galaxie et non situés dans le voisinage proche du Soleil. Les coordonnées galactiques sont un repérage effectué à l'aide d'une latitude et d'une longitude définies de telle sorte que le plan galactique correspond à l'équateur, et l'origine des longitudes corresponde au centre galactique. Le système de coordonnées galactiques est un système de coordonnées célestes qui prend en compte la rotation de la Galaxie sur elle-même. On parle ici aussi de longitude et de latitude galactiques. Le plan de référence de ce système est le plan de la Galaxie centré sur le centre galactique. Le pôle nord galactique a été défini par convention dans le repère équatorial par une ascension droite de 12 h 51 min 26,282 s et une déclinaison de 27°07′42.01″. Dans ce plan, la direction de référence de la mesure est la direction du centre de la Galaxie.
- La longitude galactique (l) est l'angle entre cette direction de référence et la projection de l'objet sur le plan de la galaxie. La longitude galactique vaut 0° dans la direction du centre de la Galaxie.
- La latitude galactique (b) est la mesure de l'angle entre le plan de référence et l'objet avec le Soleil au centre. Elle mesure en degrés la hauteur de cet objet de 0° dans le plan de référence à 90° au pôle nord galactique.
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle permet d'afficher les trois principaux systèmes de coordonnées célestes en 3D.
Résumé des propriétés des systèmes de coordonnées usuels
| Système de coordonnées | Origine | Plan fondamental | Pôles | Coordonnées | Direction principale |
|---|
| | | | Latitude | Longitude | |
| Horizontal | Observateur | Horizon | Zénith / Nadir | Élévation | Azimuth (A) | Point nord |
| Équatorial | Centre de la Terre (géocentrique) / du Soleil (héliocentrique) | Équateur céleste | Pôles célestes | Déclinaison (δ) | Ascension droite (α) | Point vernal |
| Écliptique | Écliptique | Pôles écliptiques | Latitude écliptique (β) | Longitude écliptique (λ) |
| Galactique | Centre du Soleil | Plan galactique | Pôles galactiques | Latitude galactique (b) | Longitude galactique (l) | Centre galactique |
Systèmes de coordonnées spatiaux
Dans le cadre de l'analyse de l'attitude et de l'orbite d'un satellite, certains référentiels sont particulièrement utilisés. Les plus importants d'entre eux sont présentés dans cette partie.
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle permet de visualiser dans l'espace une partie des repères spatiaux qui vous sont présentés dans cette partie.
Référentiel héliocentrique
Le référentiel de Kepler (ou référentiel héliocentrique) est le référentiel centré sur le centre de masse du Soleil et dont les axes pointent vers des étoiles fixes. Ce référentiel inertiel est utilisé pour les missions interplanétaires. Ces étoiles sont suffisamment lointaines pour qu'elles apparaissent fixes aux échelles de temps considérées.
- Le repère HSEa (pour "heliocentric solar ecliptic inertial") est un exemple de repère héliocentrique. Son axe X pointe vers le point vernal, Z vers le pôle nord écliptique et Y complète le trièdre.
Référentiel géocentrique (ECI)
Le référentiel géocentrique ("Earth Centered Inertial"ou ECI en anglais) est un référentiel dont l'origine est le centre de la Terre et dont les trois axes pointent également vers des étoiles fixes. L'origine du système se situe au centre géométrique de la Terre, l'axe Z est aligné avec le pôle nord, l'axe X pointe vers le point vernal et l'axe Y complète le trièdre. D'autres systèmes de ce type existent, définis par rapport à d'autres directions. La bonne connaissance de la position des étoiles permet de déterminer l'orientation du satellite dans ce référentiel par observation de ces étoiles.
- Parmi ces référentiels, on peut citer J2000 GCI (pour "geocentric inertial"). Son axe Z est aligné avec le pôle nord, l'axe X pointe vers le point vernal au 1er janvier 2000 et l'axe Y complète le trièdre. Ce repère est équatorial.
 Point vernal "vrai"
Point vernal "vrai"
Le point vernal "vrai" se déplace chaque année en raison de la précession des équinoxes (mouvement de l'axe de rotation de la Terre) et du lent déplacement des étoiles. De ce fait on définit un point vernal fixe conventionnel (celui du 1er janvier 2000 pour le repère J2000).
Repère instruments
Un repère instrument est aligné suivant les directions caractéristiques de l'instrument. Ces repères sont définis par rapport au repère satellite ou par rapport à un repère secondaire, lui-même défini par rapport au repère satellite. L'alignement entre les différents référentiels est mesuré sur le sol mais peut évoluer pendant le lancement, mais également à cause du changement de gravité et des distorsions thermiques. Un instrument peut d'ailleurs être positionné sur un bras articulé (cela se rencontre surtout sur les sondes planétaires). La connaissance précise de l'attitude nécessite un étalonnage en vol de ces changements d'alignement et distorsions. Les données et les commandes de la charge utile et des capteurs sont paramétrées par rapport aux systèmes de coordonnées locaux.
Représentation d'attitude
Auteur: Gary Quinsac
Introduction
L'orientation d'un satellite dans l'espace correspond à l'orientation du repère fixé sur son corps par rapport à un autre repère, tel que ceux vus précédemment. Ainsi, la détermination d'attitude d'un satellite en particulier requiert des méthodes d'estimation de la matrice orthogonale transformant des vecteurs d'un référentiel de référence fixé dans l'espace à un référentiel fixé par rapport au corps du satellite. De plus, une mission spatiale ne peut être définie par un unique référentiel. En fonction des besoins, de l'échelle à laquelle on se place, il est nécessaire d'utiliser tel ou tel référentiel. Dès lors, le passage d'un référentiel à un autre devient un aspect crucial du SCAO. L'une des plus importantes propriétés des matrices d'attitude est énoncée par le théorème d'Euler.
 Théorème d'Euler
Théorème d'Euler
L'orientation instantanée d'un objet peut toujours être décrite par une unique rotation autour d'un axe fixe.
On peut parler de pôle eulérien pour nommer le centre de rotation. Il doit son nom au mathématicien et physicien suisse Leonhard Euler. Dès lors qu'un point d'un solide reste fixe lors d'un déplacement, ce déplacement est équivalent à une rotation autour d'un axe passant par le point fixe (pôle eulérien). En algèbre linéaire, ce théorème implique que deux référentiels cartésiens partageant la même origine sont reliés par une rotation autour d'un axe fixe.
Leonhard Euler

Portrait par Johann Georg Brucker (1756).
Crédit :
Domaine public
Les relations permettant de jongler entre les systèmes de coordonnées peuvent être charactérisées de différentes manières, comportant chacune leurs lots d'avantages et inconvénients. Certaines d'entre elles sont présentées dans la partie suivante :
Les démonstrations des principales relations sont proposées en exercices.
Matrice du cosinus directeur
La façon la plus évidente de donner l'orientation d'un référentiel par rapport à un autre est d'exprimer leurs vecteurs de base dans l'autre repère.
Propriétés de la MCD
La MCD est une matrice orthogonale, ce qui signifie que son inverse est égal à sa transposée :
![[T]^{-1} = [T]^T](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation32.png) et
et ![[T][T]^T = [I] = [T]^T[T]](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation33.png)
![\bold v_R = [T]_{R|B}^T \bold v_B = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_y \cdot \bold R_x & \bold B_z \cdot \bold R_x \\ \bold B_x \cdot \bold R_y & \bold B_y \cdot \bold R_y & \bold B_z \cdot \bold R_y \\ \bold B_x \cdot \bold R_z & \bold B_y \cdot \bold R_z & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation34.png)
Les transformations successives entre référentiels peuvent être déterminées par une série de multiplications matricielles. Par exemple, la transformation du référentiel inertiel au référentiel du satellite peut être décomposée de la manière suivante : transformation du référentiel inertiel au référentiel fixé sur la Terre multipliée par la transformation du référentiel fixé sur la Terre au référentiel orbital, le tout multiplié par la transformation du repère orbital au repère du satellite.
![[T]_{sat|inertiel} = [T]_{sat|orbite} [T]_{orbite|Terre} [T]_{Terre|inertiel}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation35.png)
Limitations de cette représentation
Malgré certains avantages, la MCD n'est pas toujours la représentation la plus adaptée. Elle utilise 9 paramètres pour décrire une orientation, parmi lesquels seulement 3 sont indépendants.
Angles d'Euler
Présentation des angles d'Euler
Les angles d'Euler sont les angles introduits par Leonhard Euler pour décrire l'orientation d'un solide. Ils peuvent être utilisés pour définir l'orientation d'un référentiel par rapport à un autre. On obtient une rotation en faisant varier l'un des trois angles d'Euler et une séquence de 3 rotations est suffisante pour décrire n'importe quelle transformation. La première rotation est effectuée selon n'importe quel axe, tandis que les deux suivantes ne peuvent jamais être effectuées autour d'un axe utilisé par la rotation précédente. Au total, 12 jeux d'angles d'Euler existent : (1,2,1), (1,2,3), (1,3,1), (1,3,2), (2,1,2), (2,1,3), (2,3,1), (2,3,2), (3,1,2), (3,1,3), (3,2,1), (3,2,3). L'ordre des rotations et la valeur des angles ne sont pas uniques et sont sujets à des singularités mathématiques.
Exemples
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle permet de visualiser dans l'espace les séquences d'Euler qui sont introduites dans cette section à titre d'exemple.
- La séquence d'Euler la plus connue, nommée d'après lui, est la séquence (3,1,3). Elle a notamment été utilisée pour étudier le mouvement gyroscopique avec les trois rotations successives :
- La précession
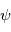 , autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).
, autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu). - La nutation
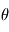 , autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).
, autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert). - La giration
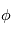 , ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
, ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
Cette séquence peut également être utilisée pour décrire les paramètres orbitaux d'un satellite par rapport au référentiel inertiel centré sur la Terre. La première rotation correspond alors à l'angle du noeud ascendant, 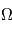 , autour de l'axe
, autour de l'axe  . La deuxième rotation est l'inclinaison,
. La deuxième rotation est l'inclinaison, 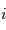 , autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie,
, autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie, 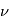 , autour de la normale à l'orbite.
, autour de la normale à l'orbite. - La séquence (3-1-2) est souvent utilisée pour décrire l'orientation d'un satellite par rapport au référentiel orbital.
- La première rotation correspond au lacet, autour du nadir.
- La suivante est le roulis, autour de l'axe
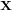 du satellite.
du satellite. - La dernière est le tangage.
Les angles d'Euler décrivent une rotation unique, ce qui est généralement un avantage par rapport à la MCD. Cependant, à une orientation donnée correspondent plusieurs jeux d'angles d'Euler.
Limites de cette représentation
D'une manière générale, les angles d'Euler déterminent une orientation unique, ce qui est un avantage sur la MCD. Des singularités apparaissent lorsque le deuxième angle d'Euler aligne les premier et troisième axes de rotation. Dans ce cas, cette description d'attitude à 3 degrés dégénère en une description à seulement 2 degrés de liberté. Cette condition est réalisée lorsque l'angle vaut 90 et 270 degrés pour les 6 rotations où les premier et troisième axes sont différents, et lorsque l'angle vaut 0 et 190 degrés pour les 6 rotations où les premier et troisième axes sont identiques.
Séquence d'Euler pour les paramètre orbitaux
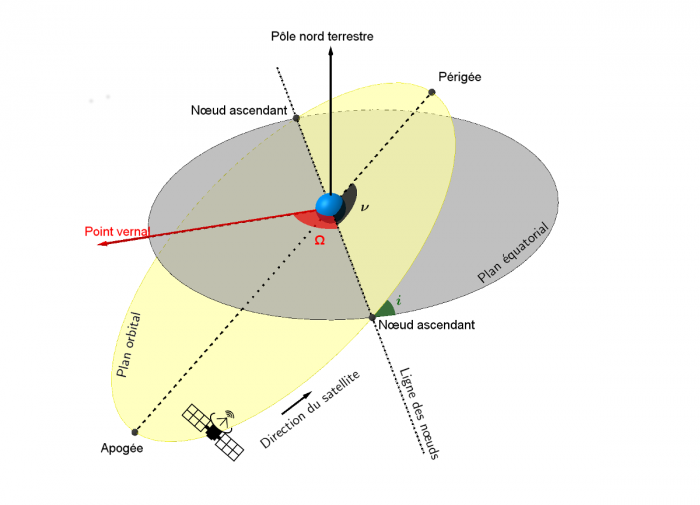
La séquence d'Euler (3-1-3) correspond aux paramètres orbitaux habituellement utilisés pour un satellite en orbite terrestre : le nœud ascendant (
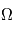
), l'inclinaison (
) et l'anomalie vraie (
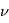
).
Crédit :
Gary Quinsac
Séquence d'Euler pour les roulis, tangage et lacet
La séquence d'Euler (3-1-2) correspond aux angles de roulis, tangage et lacet. Ils sont illustrés avec le satellite d'observation de la Terre SPOT 3.
Crédit :
Gary Quinsac
Quaternions
Auteur: Gary Quinsac
Représentation 3D
Afin de s'affranchir du problème de singularité rencontré avec les angles d'Euler, une représentation de l'attitude composée de 4 éléments est introduite sous le nom de quaternion (dont les éléments sont appelés paramètres d'Euler). Cette construction mathématique est présentée plus en détail dans la partie suivante.
Des quaternions à la MCD
De la même façon que l'on peut exprimer la MCD en fonction des angles d'Euler, elle peut être paramétrée en fonction d'un quaternion de la manière suivante :
![[T]_{B|R} = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation15.png)
Propriétés des quaternions
Avantage des quaternions
Un avantage inhérent à cette représentation est que les équations de la cinématique deviennent purement algébriques et ne contiennent plus de fonctions trigonométriques.
Présentation mathématique
Les quaternions sont un système de nombres premièrement décrits par William Rowan Hamilton en 1843 appliqué à la mécanique et à l'espace à 3 dimensions.
 William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton (04/08/1805 - 02/09/1865) est un mathématicien, physicien et astronome irlandais (né et mort à Dublin). Outre sa découverte des quaternions, il contribua également au développement de l'optique, de la dynamique et de l'algèbre. Ses recherches se révélèrent importantes pour le développement de la mécanique quantique.
William Rowan Hamilton
Peinture de Sir William Rowan Hamilton.
Crédit :
Domaine public
Définition mathématique
Un quaternion q est une expression de la forme :
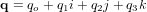
où 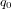 ,
,  ,
,  ,
,  sont des nombres réels, et
sont des nombres réels, et 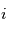 ,
, 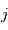 ,
, 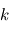 sont des symboles respectant les relations quaternioniques :
sont des symboles respectant les relations quaternioniques :
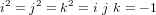
Par analogie avec les nombres complexes, 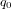 est appelé partie réelle de
est appelé partie réelle de  et
et 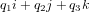 est appelé partie imaginaire.
est appelé partie imaginaire.
L'ensemble des quaternions est un espace vectoriel de dimension 4 et de base 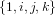 où s'applique l'addition composant par composant. Soient deux quaternions
où s'applique l'addition composant par composant. Soient deux quaternions  et
et  :
:
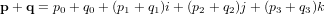
Afin d'introduire la multiplication, il faut d'abord introduire le produit hamiltonien. Les produits des éléments de base 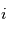 ,
, 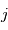 et
et 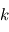 sont définis de la manière suivante :
sont définis de la manière suivante :
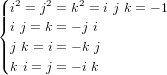
La multiplication de quaternions est associative et distributive, mais pas commutative en général. Pour les quaternions q et p elle est définie par :
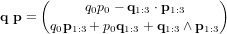
Elle peut être représentée par une multiplication matricielle. Dans ce cas, une matrice composée de valeurs du premier quaternion vient multiplier le second quaternion, tel que : ![\bold q \ \bold p = [Q(\bold q)] \bold p](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation53.png)
avec ![[Q(\bold q)] = \begin{pmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation54.png) .
.
Le conjugué, la norme et l'inverse des quaternions  et
et  sont :
sont :
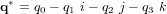 et
et 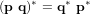
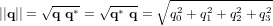 et
et 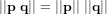
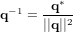
Equations du mouvement
Auteur: Gary Quinsac
Introduction à la cinématique et la dynamique
Maintenant que nous avons étudié les différentes façons de décrire l'orientation d'un repère à l'instant t, nous pouvons introduire la notion de mouvement. Les équations du mouvement sont un aspect essentiel de la conception et de la réalisation d'un système de contrôle d'attitude car elles régissent la position au cours du temps des objets considérés. Ces équations peuvent être séparées en deux catégories :
- Lorsque nous étudions l'orientation relative de deux référentiels en fonction du temps, nous sommes dans le domaine de la cinématique. Elle recouvre les aspects du mouvement qui peuvent être analysés sans considérer les forces et les couples.
- À l'instant où les forces et les couples sont introduits, on entre dans le domaine de la dynamique.
Afin de clarifier les choses, prenons une particule ponctuelle de la physique newtonienne. Si  représente sa position,
représente sa position,  sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit
sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit  . L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen
. L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen 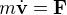 ou
ou  , avec
, avec 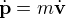 la quantité de mouvement,
la quantité de mouvement,  la résultante des forces appliquées et
la résultante des forces appliquées et  la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire
la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire  . Les forces et quantités de mouvement sont quant à elles remplacées par le couple
. Les forces et quantités de mouvement sont quant à elles remplacées par le couple  et le moment angulaire
et le moment angulaire  . La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
. La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
 Aller plus loin
Aller plus loin
Cinématique du satellite
Auteur: Gary Quinsac
Cinématique du point
La cinématique est l'étude du mouvement en fonction du temps indépendammant des causes produisant ce mouvement. Elle est utilisée pour décrire la trajectoire du centre de masse d'un satellite dans l'espace.
Cinématique et changement de référentiels
Dans notre domaine, nous sommes constamment contraints de passer d'un repère à un autre pour décrire la trajectoire d'un objet. En cas de référentiels en rotation, tels qu'un référentiel fixé par rapport à la Terre et un référentiel inertiel, passer de l'un à l'autre nécessite d'introduire des termes supplémentaires. Par exemple, si l'on veut décrire la position, la vitesse et l'accélération d'une particule dans un référentiel inertiel noté 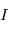 à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté
à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté 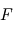 , on peut écrire :
, on peut écrire :
![\bold{r}_I = [T]_{I|F} \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation10.png)
![\bold{v}_I = \frac{d}{dt} (\bold{r}_I) = [T]_{I|F} \ \frac{d}{dt} (\bold{r}_F) + \frac{d}{dt}([T]_{I|F}) \ \bold{r}_F = [T]_{I|F} \ \frac{d}{dt}(\bold{r}_F) + ([T]_{I|F} \ [\Omega]) \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation11.png)
Nous avons utilisé la dérivée de la MCD qui est introduite dans le chapitre sur la cinématique d'attitude. Finalement :
![\bold{v}_I = [T]_{I/F} ([\Omega] \ \bold{r}_F + \bold{v}_F)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation12.png)
![\bold{a}_I = \frac{d}{dt}(\bold{v}_I) = \frac{d}{dt}([T]_{I/F}) ([\Omega] \ \bold{r}_F + \bold{v}_F) + [T]_{I/F} \left[ \frac{d}{dt}([\Omega]) \ \bold{r}_F + [\Omega] \ \frac{d}{dt}(\bold{r}_F) + \frac{d}{dt}(\bold{v}_F)\right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation13.png)
![\bold{a}_I = [T]_{I/F} \left[ [\Omega] \left([\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega] \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation14.png)
Dans le réferentiel en rotation (celui fixé par rapport à la Terre), la deuxième loi de Newton peut alors être écrite :
![\bold{F}_F = [T]_{F/I} \left( m \ \bold{a}_I \right) = m \left[ [\Omega] \left( [\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega]) \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation15.png)
où ![\frac{d}{dt} \left( [\Omega] \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation16.png) est l'accélération angulaire. On introduit ici les accélérations centripète
est l'accélération angulaire. On introduit ici les accélérations centripète ![[\Omega] \left( [\Omega] \ \bold{r}_F \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation17.png) et de Coriolis
et de Coriolis ![2 \ [\Omega] \ \bold{v}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation18.png) .
.
Cinématique d'attitude
La simulation et l'estimation d'attitude nécessitent généralement des représentations simples de l'attitude, telles que celles présentées dans le chapitre du même nom. Les équations différentielles de la cinématique peuvent ainsi être obtenues pour ces différentes représentations. Les démonstrations de ces équations sont proposées en exercices.
La cinématique d'attitude relie des vitesses angulaires à des orientations dans l'espace. Si cela peut sembler simple dans le cas d'une rotation autour d'un axe fixe, cela devient beaucoup moins intuitif dans le cas d'un mouvement plus général, où l'axe de rotation varie au cours du temps. Pour un corps en rotation autour d'un axe fixe, l'orientation par rapport à cet axe peut être déterminée en intégrant la vitesse angulaire ω, puisque 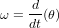 .
.
Quaternions
Dans le cas des quaternions, l'expression de l'équation de la cinématique se retrouve simplifiée :
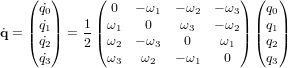
Une écriture plus compacte est possible :
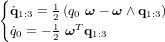
Contrairement aux angles d'Euler, les quaternions ne présentent pas de singularité géométrique. L'équation cinématique exprimée avec les quaternions ne possède pas de fonctions trigonométriques, ce qui rend les quaternions parfaitement adaptés aux calculs à bord réalisés en temps réel. Ainsi, les algorithmes de détermination d'attitude modernes sont généralement décrits en termes de quaternions.
Dynamique du satellite
Auteur: Gary Quinsac
Bases de la dynamique
Maintenant que nous nous tournons vers la dynamique d'attitude, il est important de bien différencier le mouvement de rotation d'un système du mouvement de son centre d'inertie. Nous allons nous concentrer sur le cas d'un corps rigide.
Propriétés d'inertie
Lorsque l'on parle du mouvement d'un solide autour de son centre d'inertie, il nous faut définir le tenseur d'inertie. Il s'exprime ainsi :
![[I] = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{n}{m_i \left(y_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & -\sum_{i=1}^{n}{m_i \ x_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ z_i} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+y_i^2 \right)} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation9.png) ,
,
Les éléments diagonaux de ces expressions sont les moments d'inertie du solide par rapport aux divers axes, et les autres éléments sont les produits d'inertie. Les propriétés inertielles d'un solide sont donc totalement décrites par sa masse, la localisation de son centre d'inertie (ou centre de masse), et par les moments et produits d'inertie définis par rapport à des axes de références en un point particulier. Tous les solides ont un jeu d'axes principaux d'inertie dont l'origine se trouvent en son centre de masse et qui annule les produits d'inertie, rendant diagonale la matrice d'inertie.
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle illustre l'importance du choix des axes d'inertie dans le calcul de la matrice d'inertie.
 Rappel
Rappel
Dynamique du solide
Considérons un satellite solide avec un référentiel fixé sur son corps  dont l'origine se trouve au centre de masse du satellite. Notons
dont l'origine se trouve au centre de masse du satellite. Notons  le vecteur vitesse angulaire du référentiel
le vecteur vitesse angulaire du référentiel  par rapport au référentiel inertiel
par rapport au référentiel inertiel 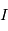 .
.
Equation d'Euler
D'après la 2ème loi de Newton, dans un référentiel galiléen, la dérivée de la quantité de mouvement est égale à la somme des forces extérieures qui s'exercent sur le solide. Dans le cas du moment angulaire, son principe de conservation stipule que sa dérivée est égale à la somme des couples extérieurs qui s'exercent sur le corps :
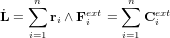
où 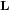 est le moment angulaire du corps solide par rapport à son centre de masse et
est le moment angulaire du corps solide par rapport à son centre de masse et 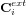 sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
Facteurs impactant l'attitude d'un satellite
Il est maintenant possible de réécrire cette équation en reprenant l'expression du moment cinétique présentée précédemment complétée par le moment angulaire stocké par n'importe quel objet en rotation dans le satellite ![\bold L = [I] \boldsymbol\omega+ \bold h](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation28.png) :
:
![[I] \dot{\boldsymbol\omega} = \sum_{i=1}^{n}{\bold C_i^{ext} - \dot{\bold h} - \dot{[I]} \boldsymbol\omega}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation29.png)
Cette dernière équation permet de comprendre comment l'attitude d'un satellite peut être modifiée. En prenant les termes de cette équation de la gauche vers la droite, on retrouve d'abord les couples extérieurs, les objets embarqués en rotation (tels que les roues à inertie) et les modifications des moments d'inertie du satellite (qui peuvent notamment être dues à la perte de carburant au cours d'une mission).
En conclusion, les couples peuvent perturber l'attitude d'un satellite mais peuvent également être utilisés pour la contrôler. Les actionneurs doivent donc avoir une capacité suffisante pour contrer les couples perturbateurs tout au long de la mission si l'on veut un contrôle permanent de l'attitude du satellite.
Perturbations
Auteur: Gary Quinsac
Perturbations : introduction
Les faibles forces agissant sur un satellite sont connues pour dégrader la précision de pointage et engendrer des déformations mécaniques.
Des perturbations de différentes origines...
On peut distinguer les perturbations externes des perturbations internes au satellite. Dans la première catégorie on retrouve la pression de radiation solaire, la trainée atmosphérique ou pression dynamique, le couple magnétique dû au dipôle résiduel et le gradient de gravité. Les perturbations internes sont liées aux équipements présents dans le satellite. Si certains sont utilisés pour contrôler le satellite, comme les roues à inertie, la plupart sont à l'origine de couples perturbateurs. Parmi ces phénomènes, on retrouve les mécanismes tels que ceux utilisés pour les panneaux solaires ou les instruments mobiles, le désalignement et la quantification des actionneurs, le déplacement du carburant, l'incertitude sur le positionnement du centre de gravité, le frottement des roues à inertie ou encore le dégazage des polymères.
Les forces extérieures sont les plus importantes pour la majorité des CubeSats car ceux-ci sont généralement dépourvus de mécanismes ou de parties mobiles. On dénombre 4 sources environmentales de couples perturbateurs dont l'intensité varie grandement en fonction de la position du satellite dans l'espace :
Ayant différents effets
On remarque que les perturbations citées précédemment peuvent avoir deux types d'effets : séculaire ou cyclique. Les perturbations ayant un effet cyclique sont en moyenne nulles sur une orbite circulaire. Les perturbations séculaires s'accumulent durant une orbite et sont analogues à une force non-conservative. Or, on se souvient que les couples extérieurs sont proportionnels à la variation du moment cinétique du satellite. La gestion du moment cinétique va donc dépendre du type de perturbation auquel le satellite aura affaire. Suivant le pointage, certaines perturbations extérieures peuvent être cycliques ou séculaires. Dans le cas d'un pointage inertiel, on parle d'effets cycliques pour la traînée atmosphérique, le gradient de gravité et les couples magnétiques, alors qu'on parle d'effets séculaires pour les couples de pression de radiation solaire. Dans le cas d'un autre pointage classique, le pointage nadir, les couples magnétiques et de pression solaire ont des effets cycliques, à l'inverse de la trainée atmosphérique. Pour ce qui est des gradients de gravité, ils peuvent avoir les deux types d'effets.
Perturbations environmentales
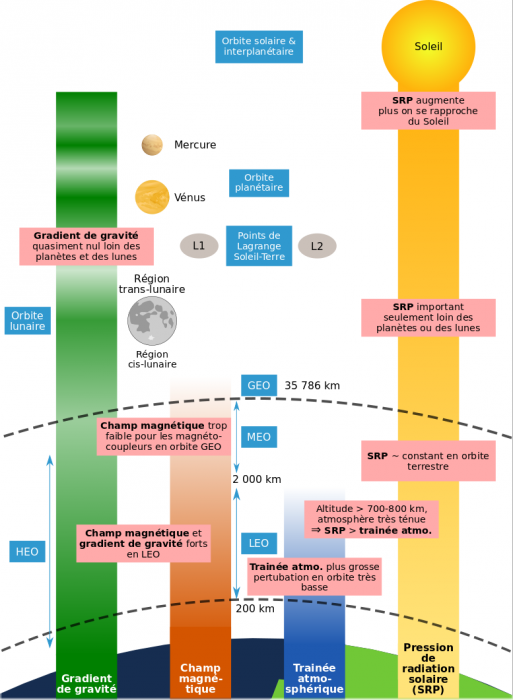
Couples perturbateurs dus à l'environement du satellite.
Crédit :
Gary Quinsac
Couples subis par un CubeSat de 3U
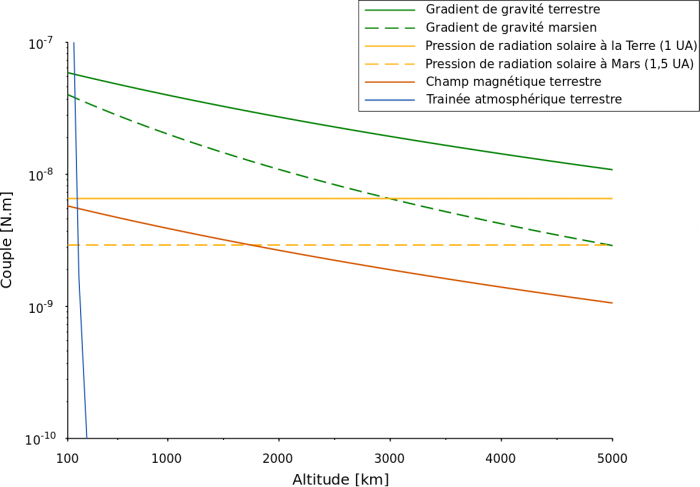
Les couples maximums subis par un CubeSat de 3U autour de la Terre et Mars sont représentés (respectivement en traits pleins et pointillés). Mars n'ayant pas ou peu de champ magnétique et une atmosphère très ténue, les couples associés ne sont pas représentés car trop faibles.
Crédit :
Gary Quinsac
Couple cyclique ou séculaire : fonction du pointage
Le couple de pression de radiation solaire est plus ou moins constant dans le cas d'un pointage inertiel, à l'origine d'une accumulation du moment cinétique : c'est un couple séculaire. Au contraire, ce couple est moyennement nul sur une orbite pour un satellite effectuant un pointage nadir : on dit alors que le couple est cyclique.
Crédit :
Gary Quinsac
Gestion du moment cinétique
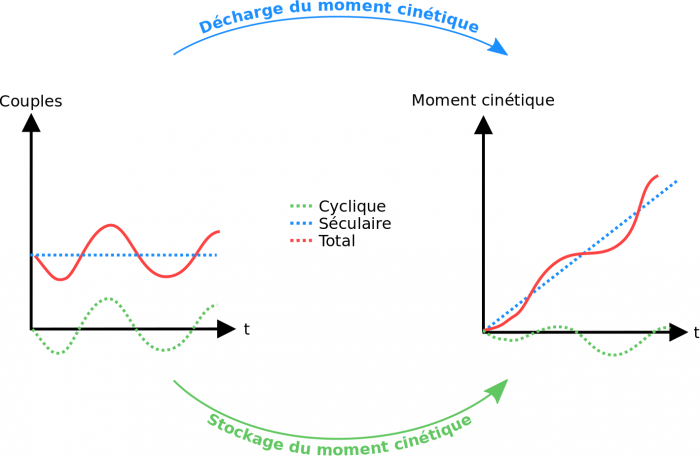
On peut voir l'accumulation du moment cinétique au cours d'une orbite dans le cas d'un couple séculaire, nécessitant de décharger celui-ci avec des actionneurs appropriés. En revanche le couple cyclique peut être stocké par un actionneur qui va se contenter de fournir un couple en opposition de phase tout au long de l'orbite.
Crédit :
Gary Quinsac
Perturbations externes
Auteur: Gary Quinsac
Champ magnétique
Certains corps célestes, dont la Terre, ont des champs magnétiques assez puissants pour induire d'importants effets dans l'espace environnant. Ce champ interagit avec tout autre champ magnétique qu'il rencontre. En général, les satellites ont eux-mêmes un certain niveau de moment magnétique résiduel qui se traduit par un champ magnétique propre relativement faible. Ils se comportent comme des dipôles magnétiques car ils sont parcourus par des boucles de courant. Ainsi, un courant de I ampères circulant dans une boucle plane d'aire A produit le moment dipolaire (en A.m) :
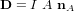
Des méthodes de compensation sont généralement mises en œuvre à bord. Si le moment magnétique résiduel d'un satellite n'est pas aligné avec le champ magnétique local un couple magnétique apparaît et modifie l'attitude du satellite. Le couple magnétique 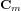 est donné par :
est donné par :
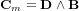
où 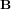 (en T) représente le champ magnétique.
(en T) représente le champ magnétique.
 Champ magnétique terrestre
Champ magnétique terrestre
Bien que le champ magnétique de la Terre soit complexe, il est souvent suffisant de le modéliser tel un dipôle (30% d'erreur sont souvent considérés) et de déterminer la valeur maximum possible. Le couple maximum peut donc être estimé à partir du champ magnétique 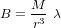 , où
, où 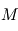 (en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique,
(en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique, 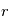 la distance entre le satellite et le centre du corps , et enfin
la distance entre le satellite et le centre du corps , et enfin 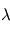 une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
Dipôle magnétique terrestre
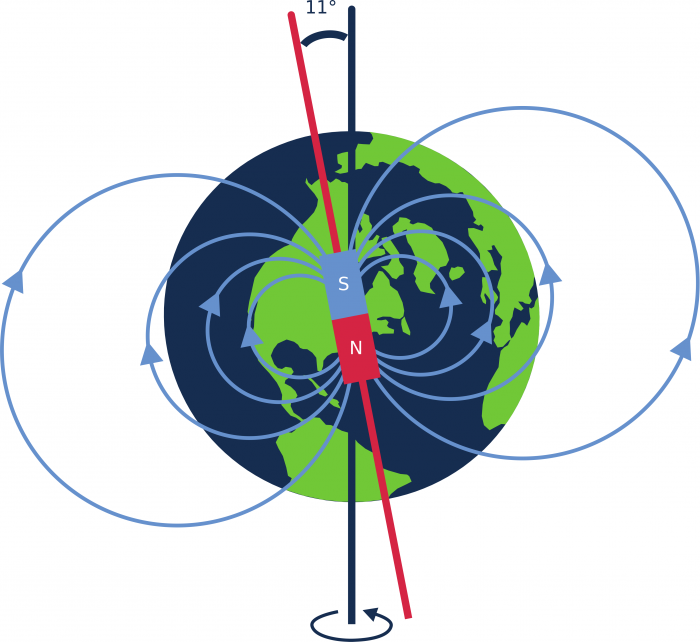
La Terre peut être assimilée à un dipôle magnétique dont l'axe est incliné d'à peu près 11° par rapport à l'axe nord-sud géographique. Attention, le pôle sud magnétique se trouve du coté du pôle nord géographique.
Crédit :
Gary Quinsac
Champ magnétique terrestre sur une orbite
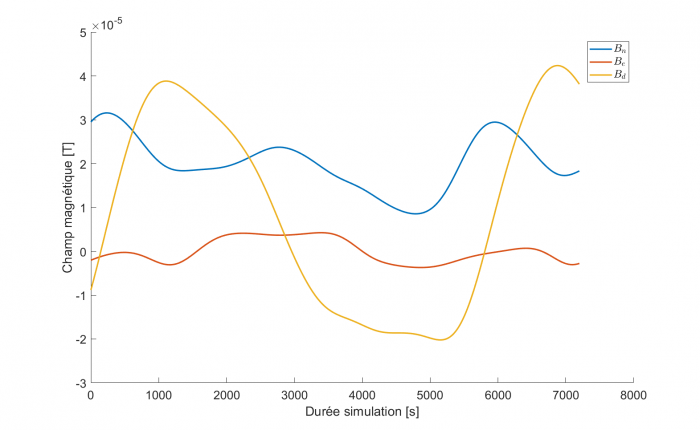
Champ magnétique sur une orbite terrestre circulaire de 500 km d'altitude et 50° d'inclinaison dans le référentiel NED.
Crédit :
Gary Quinsac
En dehors de quelques corps du système solaire, tels que la Terre et Jupiter, la plupart des régions de l'espace ne possèdent pas un champ magnétique suffisamment puissant et bien connu pour qu'un contrôle d'attitude magnétique puisse être utilisé par un satellite s'y trouvant.
 Aller plus loin
Aller plus loin
Gradient de gravité
Le gradient de gravité résulte de l'interaction du champ gravitationnel, lui-même proportionnel à l'inverse du carré de la distance, avec un satellite de masse non ponctuelle. L'accélération gravitationnelle est la plus forte sur la partie du satellite la plus proche du corps attracteur. Le gradient est à l'origine d'un couple qui peut être utilisé pour contrôler passivement l'attitude du satellite. Les couples de gradient de gravité apparaissent lorsque le centre de gravité d'un satellite en orbite n'est pas aligné avec le centre de masse par rapport à la verticale locale.
 Centres de masse et de gravité
Centres de masse et de gravité
Le centre de masse, également appelé centre d'inertie, est le barycentre des masses d'un objet. Le centre de gravité, quant à lui, est le point d'application de la résultante des forces de gravité. Si ceux-ci sont souvent confondus, ce n'est plus le cas lorsque le champ de gravitation n'est plus uniforme dans le corps en question.
On exprime le gradient de gravité 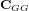 de la manière suivante :
de la manière suivante :
où 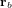 est le vecteur position allant du centre de gravité du satellite à l'élément de masse et
est le vecteur position allant du centre de gravité du satellite à l'élément de masse et 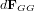 est la force de gravité s'appliquant sur ce même élément de masse :
est la force de gravité s'appliquant sur ce même élément de masse :
 est la constante gravitationnelle, elle vaut
est la constante gravitationnelle, elle vaut 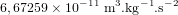 ,
, 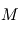 est la masse du corps attracteur et
est la masse du corps attracteur et 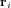 est le vecteur position de l'élément de masse
est le vecteur position de l'élément de masse 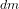 dans le référentiel inertiel (
dans le référentiel inertiel (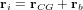 ). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
![\bold C_{GG} = \frac{3 \ G \ M}{|\bold r_{CG}|^5} \ \bold r_{CG} \wedge \left([I] \ \bold r_{CG} \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation20.png)
Ce couple dépend de la matrice d'inertie ![[I]](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation21.png) du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
 Stabilisation par gradient de gravité
Stabilisation par gradient de gravité
Cette technique de contrôle d'attitude passive est assez utilisée pour des satellites en orbite terrestre devant pointer au nadir. Elle consiste à faire intéragir un satellite de forme particulière avec le champ gravitationnel afin de contraindre son orientation. Une masse peut être montée au bout d'un mât perpandiculaire à l'orbite afin de créer un moment d'inertie minimum selon cet axe. Cette masse étant plus proche, elle est plus attirée. Le satellite aura alors tendance à aligner cet axe d'inertie vers la verticale à l'orbite (qui est la direction d'attraction gravitationnelle).
 Aller plus loin
Aller plus loin
Gradient de gravité
Géométrie du couple de gradient de gravité.
Crédit :
Gary Quinsac
Satellite stabilisé par gradient de gravité
Crédit :
National Air and Space Museum, Smithsonian Institution.
Pression de radiation solaire
La pression de radiation solaire est la source dominante de couples perturbateurs dans l'espace interplanétaire (absence de traînée atmosphérique, faibles champs de gravité et magnétique). Même en orbite basse, on a pour habitude de considérer qu'il est dominant à des altitudes supérieures à 800 km. Il est important de noter que si le Soleil n'est pas l'unique source de radiation (il y a notamment l'albédo de la Terre et de la Lune, les rayons cosmiques...), il est de loin la plus importante. Le Soleil émet des photons, mais également des protons et des électrons (vent solaire). L'interaction entre la lumière du Soleil et la surface du satellite est habituellement modélisée comme une force de pression exercée sur un objet.
On modélise la surface du satellite comme une collection de  surfaces d'aire
surfaces d'aire 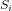 , dont la normale orientée vers l'extérieur est notée
, dont la normale orientée vers l'extérieur est notée 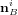 dans le référentiel du satellite et de coefficient de réflexion
dans le référentiel du satellite et de coefficient de réflexion 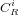 (on lui attribue généralement une valeur de 0,6 pour un petit satellite).
(on lui attribue généralement une valeur de 0,6 pour un petit satellite).
Le vecteur allant du satellite au Soleil dans le référentiel du satellite s'écrit  . L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
. L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
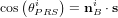
La force de pression de radiation solaire exercée sur une surface peut alors s'exprimer de la manière suivante :
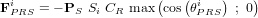 avec
avec 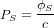
où 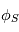 (en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et
(en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et  (en m/s) est la vitesse de la lumière.
(en m/s) est la vitesse de la lumière.
La différence entre les positions des centres de pression solaire et de masse aboutit à un couple de radiation solaire. Une telle différence dépend des surfaces éclairées, de l'incidence des rayons lumineux et de la répartition de la masse à l'intérieur du satellite. On note 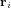 le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
 Complément : coefficients de réflexion
Complément : coefficients de réflexion
Afin de gagner en précision, il est possible de détailler le coefficient de réflexion en une somme de trois coefficients dont le résultat vaut 1 :
La force de pression de radiation sur la ième surface s'exprime alors :
![\bold F_{PRS}^i = -P_S \ S_i \left[ 2 \left( \frac{R_{diff}^i}{3} + R_{spec}^i \ \textup{cos} \left(\theta_{PRS}^i \right) \right) \bold n_B^i + \left( 1-R_{spec}^i \right) \bold s \right] \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation37.png)
 Zone d'ombre
Zone d'ombre
Afin de simuler la pression de radiation solaire, il ne faut pas oublier les zones d'ombres dans lesquelles le satellite peut se retrouver. Par exemple, en orbite basse autour de la Terre, un satellite peut passer une partie importante de son orbite caché des rayons du Soleil. L'approche la plus simple est de considérer que l'ombre de la Terre est une projection cylindrique du diamètre de la Terre le long de l'axe Soleil-Terre. Sur cette figure on remarque qu'en faisant le produit scalaire de vecteur unitaire  (Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
(Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
Géométrie du couple de pression de radiation solaire
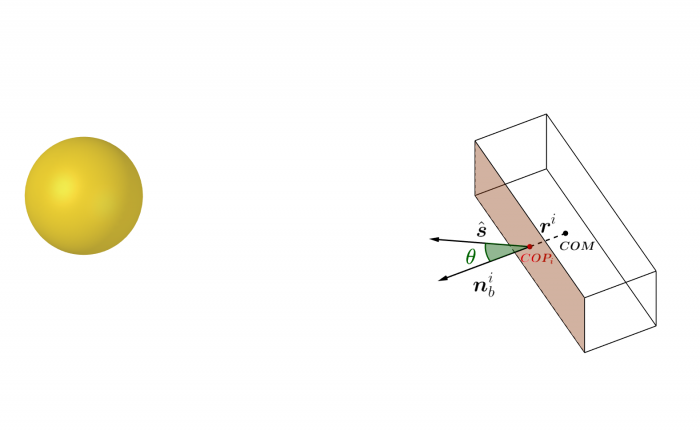
Géométrie du couple de pression de radiation solaire. Chaque face du satellite exposée au Soleil subit une force qui, si elle est désaxée par rapport au centre de masse, engendre un couple.
Crédit :
Gary Quinsac
Zones d'ombre
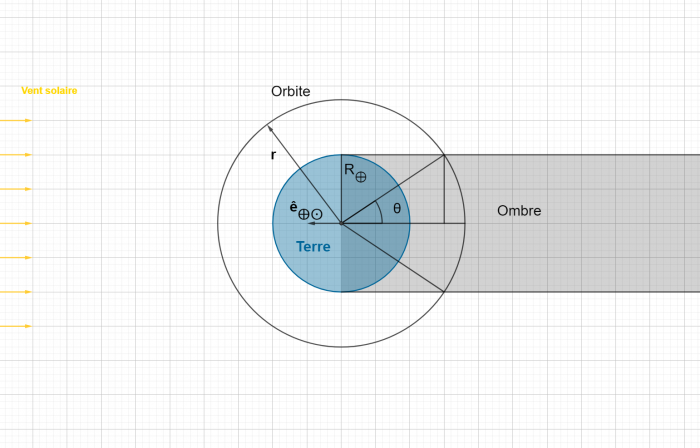
Géométrie simplifiée du problème de zone d'ombre en orbite terrestre.
Crédit :
Gary Quinsac
Traînée atmosphérique
L'atmosphère ténue des corps célestes peut exercer une force de pression sur un satellite. Cela inclut toutes les interactions avec des particules non-chargées, comme les queues de comète, les poussières ou les éjectas. Dans le cas de la Terre, à quelques centaines de kilomètres d'altitude, ce couple peut être le plus important. De la même manière qu'avec le couple dû à la pression de radiation solaire, on calcule la force exercée par la traînée atmosphérique en considérant que le satellite est une collection de N surfaces d'aire Si. On définit de nouveau la normale orientée vers l'extérieur, notée 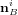 , pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
, pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
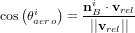
La force aérodynamique s'exerçant sur la ième surface est :
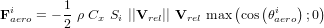
Dans cette équation, ρ est la densité atmosphérique et 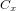 est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
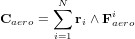
où 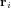 est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
En principe, les couples aérodynamiques peuvent être utilisés pour effectuer un contrôle passif de l'attitude, comme les plumes d'une flèche, et même pour un contrôle actif avec des surfaces amovibles.
Perturbations internes
Bien que les CubeSats puissent généralement être modélisés comme un simple corps solide, de nombreuses raisons peuvent rendre la situation beaucoup plus complexe :
- Certains satellites peuvent être composés de nombreux corps solides en mouvement de rotation ou de translation les uns par rapport aux autres. La dynamique des corps flexibles utilise généralement des méthodes de calcul par éléments finis. Parmi les raisons simples empêchant de traiter un satellite comme un corps rigide, on peut citer la présence de roues à inertie, de gyroscopes, de panneaux solaires motorisés ou de systèmes de déploiement.
- Le déplacement des fluides, tels que le carburant ou les fluides cryogéniques est également une source de perturbations internes.
- Les désalignements et la quantification des actionneurs peut aussi être une source de perturbations. Par exemple, un système de propulsion dont l'axe de poussée serait décalé par rapport à l'axe idéal créera des couples non désirés à chaque fois qu'il sera utilisé.
On qualifie ces couples internes de couples d'échange de moment cinétique car ils correspondent à un échange de moment cinétique entre des composants d'un satellite complexe sans que le moment cinétique du satellite dans son ensemble ne soit modifié.
Matériel
Auteur: Gary Quinsac
Introduction aux capteurs et actionneurs
Capteurs
Les capteurs se trouvent en amont de la chaîne du SCAO. Historiquement, les progrès réalisés se sont concentrés sur leur résolution et leur précision, leur masse, leur taille et leur puissance. À partir d'une référence, un capteur déduit son orientation dans l'espace ou sa vitesse de rotation. Le choix d'un capteur dépend de nombreux paramètres techniques, parmi lesquels :
- les sources de référence disponibles :
- les références externes : les étoiles, le Soleil, la Terre, le champ magnétique local,
- la référence inertielle absolue (phénomènes d'inertie par conservation du moment cinétique),
- l'orbite de la mission et les modes de pointage,
- les exigences fonctionnelles et de performances.
Les capteurs se basent sur différents types de mesures permettant ainsi de les classer :
Actionneurs
Les actionneurs sont des dispositifs conçus pour engendrer des forces ou couples capables de produire des mouvements du satellite. Les solutions existantes sont relativement variées et les principales peuvent être classées de la manière suivante :
Les actionneurs peuvent également être séparés en deux catégories. Ceux qui ne servent qu'au contrôle d'attitude, et ceux qui peuvent réaliser à la fois du contrôle d'attitude et du contrôle d'orbite.
Capteurs
Auteur: Gary Quinsac
Capteurs optiques
Les capteurs optiques fournissent l'orientation dans l'espace du repère du capteur, lui-même lié au repère du satellite, par rapport à des directions de références extérieures, telles que les étoiles, le Soleil et la Terre.
Capteurs stellaires
Un viseur d'étoiles ou capteur d'étoiles est un instrument optique qui repère les coordonnées d'une ou plusieurs étoiles et les compare ensuite aux éphémérides des étoiles enregistrées dans une bibliothèque inclue dans l'instrument. C'est l'instrument optique le plus précis (entre 1 et 10 secondes d'angle pour les plus performants). Il se compose d'un baffle afin d'éviter l'illumination par des éléments parasites tels que le Soleil, d'une partie optique chargée de collecter et focaliser la lumière sur un détecteur (CCD ou APS), d'une électronique de traitement du signal et d'un refroidisseur pour le détecteur. La matrice du détecteur est constituée de pixels qui permettent d'obtenir une image numérisée du champ de vue de l'instrument, chaque pixel étant repéré par ses coordonnées dans le repère lié au viseur stellaire. On détermine finalement la position d'une étoile en calculant le barycentre de l'énergie collectée sur les pixels éclairés. Les viseurs d'étoiles sont utilisés lorsqu'une connaissance fine de l'attitude est nécessaire. Ils ont besoin que la vitesse de rotation du véhicule soit contrôlée en amont afin de ne pas dépasser la vitesse de décrochage, vitesse au dessus de laquelle la lumière d'une étoile se trouve projetée sur de trop nombreux pixels durant la pose et ne permet plus la mesure.
Un capteur d'étoiles possède deux modes d'opération : le mode d'acquisition et le mode de suivi. Dans le premier, la position et la magnitude des objets brillants éclairant la matrice du détecteur sont comparées au catalogue d'étoiles afin de déterminer de façon grossière l'attitude du satellite sans information préalable. Une fois cette estimation de l'attitude intiale effectuée, le second mode permet le suivi sur la matrice des positions des étoiles identifiées. En sortie, un tel capteur est capable de fournir un quaternion d'attitude du repère capteur par rapport à un repère inertiel, tel que le repère J2000, et dans certains cas la vitesse de rotation du satellite.
Viseur d'étoile

Viseur d'étoiles ASTROP APS développé par l'agence spatiale nationale allemande DLT et la compagnie Jena-Optronik en Allemagne. Il est équipé d'une technologie de protection de radiation permettant de longues missions.
Crédit :
ESA, Jena-Optronik
Capteurs solaires
Les capteurs solaires permettent de déduire l'attitude du satellite de la mesure de l'angle d'incidence des rayons solaires sur le capteur. Ils sont classés en deux catégories : les capteurs analogiques et les capteurs digitaux. Dans les grosses missions satellitaires, ils permettent respectivement d'obtenir une précision de 1° à 0,1° et inférieure à 0,05°.
- Les capteurs solaires analogiques sont les plus utilisés pour les CubeSats car ils sont fiables, passifs et peu coûteux. Leur faible précision, généralement de l'ordre de quelques degrés pour cette filière, est avant tout limitée par l'albédo terrestre. Sur de plus gros satellites, ils sont essentiellement utilisés pour les modes d'acquisition/survie. Ils se composent d'une ou plusieurs photo-diodes qui convertissent l'énergie reçue, fonction de l'inclinaison solaire, en courant électrique. Ce courant est proportionnel au cosinus de l'angle entre la normale au capteur et les rayons solaires. Ainsi,
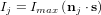 si
si 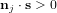 et
et 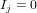 si
si 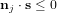 , avec
, avec 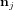 le vecteur unité pointant vers la normale extérieure à la photocellule
le vecteur unité pointant vers la normale extérieure à la photocellule  et
et  le vecteur unité allant du satellite au Soleil. Le champ de vue est un cône d'ouverture limitée.
le vecteur unité allant du satellite au Soleil. Le champ de vue est un cône d'ouverture limitée. - Les capteurs solaires digitaux utilisent l'illumination de quelques pixels d'un capteur numérique CCD ou CMOS. L'ouverture est une fente étroite, et éventuellement la lumière solaire préalablement filtrée pour ne pas abîmer les capteurs trop sensibles. La position du ou des pixels éclairés permet de déterminer l'angle d'incidence du rayon de soleil. Le principe est généralisable à 2 axes. Ils sont généralement embarqués par des satellites n'ayant pas de capteur stellaire.
Capteur solaire digital

Capteur solaire analogique pyramidal développé par NTO pour la plateforme de satellites de télécommunication Spacebus-4000. Il fournit la position du Soleil selon 2 axes avec une précision meilleure que 0,1°.
Crédit :
ESA, NTO
Capteurs terrestres
Les capteurs terrestres sont utilisés pour déterminer l'orientation du satellite par rapport à la Terre. Plus précisément, c'est l'horizon de la Terre qui est utilisé, car la Terre elle-même peut couvrir jusqu'à 40% de l'espace environnant pour un satellite en orbite passe. Néanmoins, il est difficile de détecter précisément la limite de l'horizon à cause de l'atmosphère terrestre (jusqu'à 70 km), de la décroissance graduelle de l'énergie réémise par la Terre, des variations entre les régions illuminées ou à l'ombre, et enfin de la limite de précision des capteurs. Le principe de détection adopté est donc basé sur une variation thermique de l'élément sensible dans la bande spectrale infra-rouge où la Terre est vue comme un disque uniforme : la bande d'absorption du CO2 entre 14 et 16 μm. Ainsi, l'énergie émise par la Terre est plus homogène et l'horizon, précisément délimité, est visible de jour comme de nuit.
Ces capteurs peuvent être de deux types : les capteurs statiques, qui pointent dans une direction fixe, et les capteurs à balayage. Ils sont principalement utilisés sur des satellites en orbite basse et les satellites de télécommunication en orbite GEO ou MEO. Ils ont jusqu'à présent été assez peu utilisés sur CubeSats.
Capteurs magnétiques
Magnétomètres
Les magnétomètres convertissent un champ magnétique ambiant en tension électrique. Ils sont principalement constitués de bobines conductrices qui génèrent un courant ou une variation de courant lorsqu'elles sont placées dans un champ magnétique. Ils ne possèdent pas de partie mobile, n'ont pas besoin d'un champ de vue dégagé, consomment peu et sont faiblement encombrants. Ils peuvent néanmoins être contaminés par le champ magnétique local créé par des matériaux ferromagnétiques ou des boucles de courant dans les panneaux solaires. Ainsi, il faut compenser ces champs locaux s'ils sont connus, ou s'en affranchir en se plaçant à bonne distance (au bout d'un mât par exemple) dans le cas contraire. La technologie la plus utilisée, "flux gate", délivre directement la projection du champ magnétique selon l'axe de la bobine, contrairement aux magnétomètres à induction qui fournissent la dérivée temporelle de la projection du champ magnétique. Ces capteurs étant monoaxiaux, on associe généralement trois magnétomètres orientés orthogonalement afin de mesurer le vecteur champ magnétique instantané.
Les magnétomètres sont limités à des environnements possédant un champ magnétique suffisamment fort, et donc à l'orbite terrestre basse du fait de la décroissance en  de son champ magnétique (
de son champ magnétique (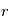 étant l'altitude du satellite). On les utilise de différentes manières, l'une d'entre elles étant de calculer le champ magnétique instantané afin de mieux calibrer les couples à générer par les magnétocoupleurs. Ils servent surtout à restituer l'attitude du satellite avec une précision de quelques degrés du fait des erreurs de modélisation du champ magnétique, des erreurs d'orbitographie et de celles propres au capteur. Dans ce cas, seule la connaissance de deux axes est disponible, l'orientation autour du champ magnétique n'étant pas observable. Enfin, on peut utiliser la dérivée du champ magnétique afin d'obtenir une mesure sur 2 axes de la vitesse angulaire du satellite.
étant l'altitude du satellite). On les utilise de différentes manières, l'une d'entre elles étant de calculer le champ magnétique instantané afin de mieux calibrer les couples à générer par les magnétocoupleurs. Ils servent surtout à restituer l'attitude du satellite avec une précision de quelques degrés du fait des erreurs de modélisation du champ magnétique, des erreurs d'orbitographie et de celles propres au capteur. Dans ce cas, seule la connaissance de deux axes est disponible, l'orientation autour du champ magnétique n'étant pas observable. Enfin, on peut utiliser la dérivée du champ magnétique afin d'obtenir une mesure sur 2 axes de la vitesse angulaire du satellite.
Magnétomètre monoaxial "fluxgate"

Un magnétomètre "fluxgate" génère son propre champ magnétique. En inversant régulièrement la direction du courant, on inverse le champ magnétique, ce qui permet d'obtenir un champ magnétique moyen nul. Dans le cas où la magnétomètre se trouve dans un champ magnétique ambiant, la moyenne n'est plus nulle et il est alors possible de connaître ce champ extérieur.
Crédit :
Wikipedia
Capteurs inertiels
Les capteurs inertiels fournissent au satellite une mesure par rapport à une référence fixe dans l'espace. Les gyromètres délivrent l'attitude (vitesse angulaire) et les accéléromètres la position par rapport à cette référence. Pour les premiers, il y a détection du mouvement de rotation absolue, tandis que pour le second c'est le mouvement de translation accéléré qui est détecté. Nous ne nous intéresserons pas ici aux accéléromètres qui ne sont pas utiles à la détermination d'attitude.
Gyromètres
Les gyromètres mesurent donc les vitesses angulaires du satellite. On peut en déduire l'attitude de celui-ci en intégrant les vitesses calculées sur un temps donné. Ils sont très intéressants car ils permettent de fournir en permanence les mesures de vitesse de rotation sans se soucier du champ de vue et avec une très bonne précision à court terme. Ils fournissent également des informations à plus haute fréquence que les autres capteurs, ce qui est nécessaire pour certaines boucles de contrôle comme pour le contrôle du vecteur de poussée lors de phases de propulsion. On distingue plusieurs types de gyromètres : les gyromètres mécaniques, les gyromètres optiques et les gyromètres vibrants.
Gyromètres mécaniques
Les gyromètres mécaniques utilisent une toupie gyroscopique. Celle-ci possède une raideur gyroscopique du fait d'une vitesse de rotation élevée permettant de la maintenir selon une direction fixe. Tout couple s'exerçant celui-ci provoque l'écartement de cet axe par rapport à la direction initiale avec une vitesse faible du fait de la rigidité gyroscopique. Le principe consiste à estimer les mouvements du véhicule par rapport à la direction de référence que matérialise l'axe de rotation de la toupie.
Gyroscope

Exemple de gyroscope. Tant que le rotor (plateau central) sera en rotation, il gardera son axe de rotation fixe quelles que soient les orientations des cercles extérieurs.
Crédit :
Gary Quinsac
Gyromètres optiques
Les gyromètres optiques peuvent être des gyromètres laser ou à fibre optique. Dans les deux cas, ils présentent l'avantage de se dispenser de pièce mécanique en mouvement (pas d'usure), d'avoir de plus grande dynamique de mesure et bande passante, une insensibilité à l'accélération et moins de contraintes concernant la stabilité en température. Les gyromètres laser fonctionnent suivant le principe du laser à cavité résonnante. Les gyromètres à fibre optique reprennent l'effet Sagnac. Deux ondes parcourant un chemin fermé en rotation (par rapport à un référentiel inertiel) subissent un décalage temporel lorsqu'elles ont été émises et reçues par un émetteur/récepteur fixe par rapport au chemin optique. Le décalage temporel entre les deux rayons lumineux est ainsi proportionnel à la vitesse de rotation du système.
Gyromètre optique
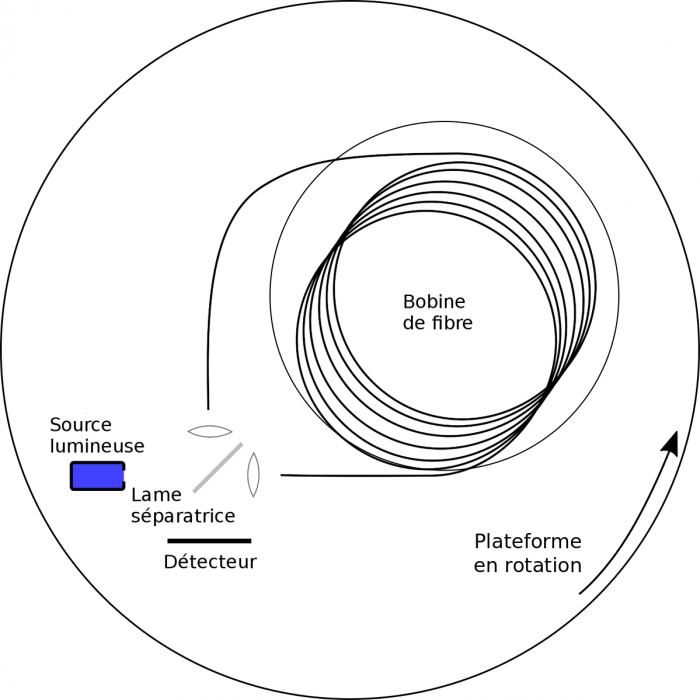
La lumière émise par la source se propage dans la bobine de fibre optique dans deux directions opposées suite à une première traversée de la lame séparatrice (un quart de l'énergie émise initialement arrivera sur le détecteur selon chacune des directions de parcours). Du fait de la rotation de la plateforme, les signaux lumineux parcourant la bobine de fibre dans des directions opposées arriveront au récepteur dans des temps différents. C'est l'effet Sagnac.
Crédit :
Gary Quinsac
Gyromètres vibrants
Les gyromètres vibrants quant à eux sont assez proches des gyromètres mécaniques, à la différence près qu'aucune pièce n'est ici en mouvement. Ils détectent le déplacement d'une onde vibratoire dans une structure, dû à la force de Coriolis.
Accéléromètres
Les accéléromètres sont principalement utilisés pour la navigation et le guidage des véhicules de rentrée atmosphérique ou dans l'identification de microvibrations. Une modification de leur tension de sortie est traduite en accélération. Le principe de base consiste à disposer d'une masse dans un boîtier fixée par des ressorts. Lorsque le boîtier est accéléré, la masse a tendance à rester fixe par inertie : elle est donc en mouvement par rapport au boîtier. Les ressorts ont alors pour effet de contrer le déplacement de la masse par rapport au boîtier, et ce déplacement devient alors proportionnel à l'accélération de ce dernier. Les accéléromètres sont capables de mesurer la résultante des forces de surface mais pas les accélérations d'origine gravitationnelle puisque la masse et son boîtier sont soumis au même champ gravitationnel.
Accéléromètre
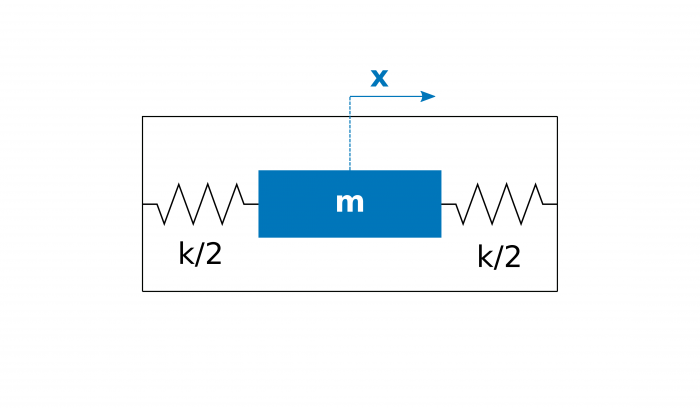
Le déplacement de la masse par rapport à la boîte dans lequelle elle se trouve dépend de l'accélération de la boîte.
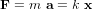
, avec

l'accélération,
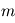
la masse,
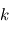
la constante de raideur du ressort et

le déplacement du ressort.
Crédit :
Gary Quinsac
Actionneurs
Auteur: Gary Quinsac
Actionneurs inertiels
Parmi les actionneurs inertiels, on distingue les roues d'inertie et les actionneurs gyroscopiques.
Roues à inertie
Les roues à inertie sont les actionneurs les plus utilisés pour le contrôle d'attitude des satellites. Elles permettent le stockage et la restitution du moment cinétique. Elles sont composées d'une masse en rotation autour d'un axe fixe ou volant d'inertie. Le couple créé par une roue à inertie est égal au changement du moment cinétique durant un temps donné (voir la page sur la dynamique d'attitude). Un couple est ainsi créé lorsque le moment cinétique de la roue à inertie est modifié, c'est-à-dire que sa vitesse de rotation change. Cette accélération ou décélération angulaire permet d'emmagasiner ou de libérer du moment cinétique. Ce type d'actionneur peut saturer, c'est-à-dire atteindre une limite supérieure ou inférieure en vitesse angulaire. Dans ce cas il lui devient impossible de fournir un couple selon cet axe (toute évolution possible est une décélération de la roue entraînant un couple dans le sens contraire à celui souhaité). Il faut alors utiliser un autre actionneur à bord pour ramener la vitesse dans une plage admissible tant pour le fonctionnement propre de la roue que pour les performances du contrôle d'attitude. Ces actions de réduction de la vitesse absolue du volant d'inertie, appelées "désaturation", se font lors de l'application d'un couple antagoniste, généralement à l'aide de magnéto-coupleurs ou de propulseurs.
Roues à inertie

Deux des quatre roues à inertie du télescope Kepler durant l'assemblage. Elles sont inclinées différemment afin de permettre un contrôle de l'attitude selon plusieurs axes. L'une de ces roues a été victime d'un problème que l'on rencontre parfois avec ce type d'actuateurs, c'est à dire une friction trop importante. Pour parer à la perte d'une roue à inertie, on se permet généralement des configurations redondantes sur les gros satellites.
Crédit :
Ball Aerospace photo
Actionneurs gyroscopiques
Les roues à inertie sont limitées en termes de capacité de couple. C'est la raison pour laquelle les satellites nécessitant de rapides manœuvres ou possédant des fortes inerties (comme les stations orbitales) utilisent plutôt des actionneurs gyroscopiques, ou gyrocoupleurs. Contrairement aux roues à inertie, le principe n'est plus de produire un couple en faisant varier la vitesse de rotation de la roue, mais en modifiant l'axe de rotation d'une roue tournant à une vitesse constante. Une variation du moment cinétique est ainsi créée, se traduisant par un couple perpendiculaire au moment cinétique de la roue et au vecteur vitesse de rotation qui lui est appliqué (suivant le principe du couple gyroscopique). Les actionneurs gyroscopiques consomment moins d'énergie et possèdent une plus grande capacité de couple pour des masses et des tailles comparables. Néanmoins, leur utilisation est limitée par l'importance des couples appliqués aux articulations (risques de panne mécanique) et aux précisions requises dans les mesures de position et de vitesse angulaire.
Actionneur gyroscopique
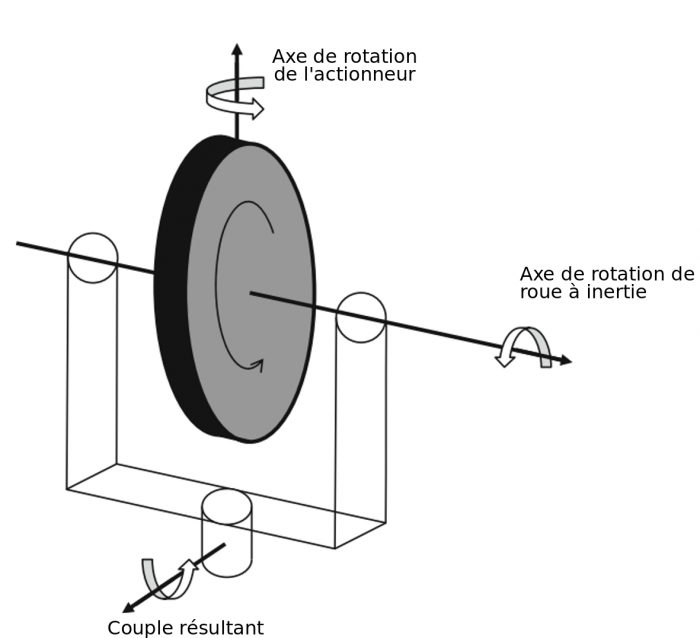
Fonctionnement d'un actionneur gyroscopique.
Crédit :
Gary Quinsac
Actionneurs magnétiques
Magnéto-coupleurs
Un magnéto-coupleur est une bobine qui, parcourue par un courant, génère un moment dipolaire 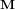 (en A.m2). En présence d'un champ magnétique tel que le champ magnétique terrestre
(en A.m2). En présence d'un champ magnétique tel que le champ magnétique terrestre  , le magnéto-coupleur fournit alors un couple
, le magnéto-coupleur fournit alors un couple 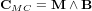 . On distingue trois types de magnéto-coupleurs :
. On distingue trois types de magnéto-coupleurs :
- Le moment dipolaire des magnéto-coupleurs les plus simples s'exprime en fonction de nombre de spires
 , de l'aire de la section de la bobine
, de l'aire de la section de la bobine  et du courant d'intensité
et du courant d'intensité 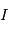 la parcourant. Ce moment dipolaire s'exprime alors
la parcourant. Ce moment dipolaire s'exprime alors 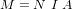 et est orienté perpendiculairement au plan de la bobine. Il est ainsi nécessaire d'effectuer de nombreux tours ou d'augmenter la section de la bobine si l'on veut obtenir un moment dipolaire plus important à intensité égale.
et est orienté perpendiculairement au plan de la bobine. Il est ainsi nécessaire d'effectuer de nombreux tours ou d'augmenter la section de la bobine si l'on veut obtenir un moment dipolaire plus important à intensité égale. - On utilise également des "torque rods", c'est-à-dire une bobine entourant cette fois un barreau ferromagnétique, afin d'obtenir de plus importants moments dipolaires pour un courant donné.
- Enfin, on réalise également des magnéto-coupleurs "embarqués", c'est-à-dire qu'ils sont directement obtenus sur le PCB où la bobine vient prendre la place des traves de cuivre de la plaque. La bobine prend alors la forme d'une spirale carrée.
La principale limitation de cet actionneur est que le couple généré est toujours orthogonal au champ magnétique, limitant à seulement deux angles d'attitude le contrôle du satellite en un point donné de son orbite. À l'instar des magnétomètres, leur utilisation est limitée aux orbites terrestres basses. Ils peuvent être utilisés soit pour effectuer du contrôle d'attitude soit pour "désaturer" des actionneurs inertiels. La plupart des applications des magnéto-coupleurs utilisent trois appareils produisant des couples sur trois axes orthogonaux. Il n'est pas toujours nécessaire d'employer plus de magnéto-coupleurs pour la redondance puisqu'ils ont habituellement un "double enroulement" fournissant une redondance interne.
Magnéto-coupleurs
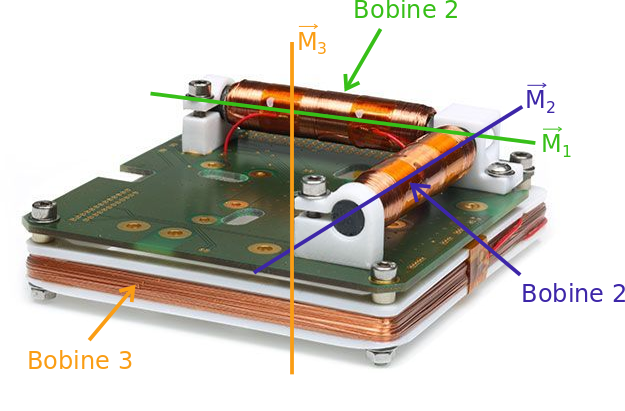
"SatBus MTQ" est un système composé de trois magnéto-coupleurs orthogonaux respectant le standard CubeSat. Les bobines 1 et 2 bénéficient d'un barreau ferromagnétique, contrairement à la bobine 3.
Crédit :
Nano Avionics
Propulsion
Auteur: Gary Quinsac
Introduction à la propulsion
Spécificités de la propulsion
Parmi les fonctions couvertes par le SCAO il y a la réalisation des manœuvres de modification de la vitesse ainsi que le contrôle d'attitude associé (assurer le pointage des propulseurs lors de la poussée). Le ΔV nécessaire au contrôle d'orbite ne peut être fourni que par des propulseurs, néanmoins ceux-ci peuvent également être utilisés pour générer des couples. Contrairement aux magnéto-coupleurs, ce sont des actionneurs utilisables sur n'importe quelle orbite car ils n'ont pas besoin d'un environnement particulier pour fonctionner. Leur principal inconvénient est une durée de vie limitée inhérente à l'utilisation d'un carburant, lui-même en quantité finie.
Fonctions de la propulsion satellitaire
Il faut différencier la propulsion des lanceurs de celle des satellites. La première doit permettre des incréments de vitesse de l'ordre de 7 à 100 km/s et de très importants niveaux de poussée. Elle se caractérise par une faible capacité d'emport et se présente sous la forme de puissants propulseurs chimiques. La seconde, qui nous intéresse ici, sert à effectuer des transferts orbitaux et des voyages interplanétaires, du contrôle d'orbite et du contrôle d'attitude. Le sous-système propulsif d'un satellite remplit ainsi certaines fonctions :
- le transfert du véhicule de l'orbite d'injection lanceur à son orbite définitive,
- le maintien à poste (contrôle d'orbite),
- le contrôle d'attitude,
- la désorbitation du véhicule en fin de vie opérationnelle,
- le transfert interplanétaire et la mise en orbite autour d'un corps (planète, astéroïde, comète...) dans le cas d'une sonde interplanétaire.
Orientation du vecteur de poussée
Pour cela, il doit délivrer des forces et des couples. Les forces, ou poussées, sont obtenues par l'éjection de matière à grande vitesse et varient entre quelques μnewtons et quelques centaines de newtons. Suivant les axes de poussée, deux cas de figure sont possibles :
- si l'axe de poussée est parfaitement aligné avec le centre de masse alors on modifie uniquement la vitesse du véhicule,
- si l'axe de poussée n'est pas aligné avec le centre de masse, il y a à la fois une modification de la vitesse du véhicule (égale au cas où la force serait apliquée au centre de masse) et de sa vitesse de rotation (apparition d'un couple proportionnel à l'écart entre l'axe et le centre de masse).
Moteur principal de la navette américaine

Test d'allumage du moteur principal de la navette spatiale.
Crédit :
NASA
Système de propulsion de BepiColombo

Vue d'artiste du système de propulsion ionique qui sera utilisé pour la mission BepiColombo. Cette mission d'exploration de la planète Mercure doit être lancée en octobre 2018 et est développée conjointement par l'ESA et la JAXA.
Crédit :
ESA
Fondamentaux de la propulsion
Incrément de vitesse
Ecrivons que la variation de la quantité de mouvement du satellite est opposée à la variation de la quantité de mouvement du carburant expulsé : 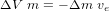
On peut directement en déduire la capacité d'incrément de vitesse total (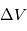 ) du satellite :
) du satellite : 
On en déduit l'équation de Tsiolkovski : 
 Manœuvres orbitales
Manœuvres orbitales
Voici quelques exemples d'incréments de vitesse associés à des lancements et à des manœuvres orbitales issus de "Spacecraft propulsion - A brief introduction" par Peter Erichsen :
Incréments de vitesses associés à des manœuvres spatiales et de décollage
| Manœuvre | ΔV typique [m/s] |
|---|
| Kourou → LEO (équatorial) | 9300 |
| Kourou → GTO | 11443 |
| Cap Canaveral → LEO (équatorial) | 9500 |
| Cap Canaveral → GEO | 13600 |
| LEO → GEO (changement d'inclinaison de 28°) | 4260 |
| GTO → GEO (changement d'inclinaison de 9°) | 1500 |
| GTO → GEO (changement d'inclinaison de 28°) | 1800 |
| Maintien à poste Nord/Sud | 50 / an |
| Maintien à poste Est/Ouest | 5 / an |
| LEO → Orbite de libération terrestre | 3200 |
| LEO → Orbite lunaire | 3900 |
| LEO → Orbite martienne | 5700 |
Quantité de carburant
Si l'on veut déterminer la quantité de carburant nécessaire à la réalisation d'un manœuvre spatiale  , il ne reste plus qu'à déplacer les termes de l'équation précédente afin d'obtenir :
, il ne reste plus qu'à déplacer les termes de l'équation précédente afin d'obtenir : 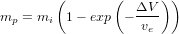
Impulsions
Nous pouvons maintenant définir de nouveaux termes. L'impulsion minimum (ou "impulse bit" en anglais, Ibit) est la plus petite modification de la quantité de mouvement permise par le système de propulsion. C'est un paramètre important lorsque l'on veut effectuer du contrôle fin de l'attitude et de l'orbite.
L'impulsion totale (Itot) quant à elle représente la capacité de modification de la quantité de mouvement pour une quantité donnée de carburant : ![I_{tot} = \int_{0}^{\tau}{F \ dt} = v_e \ \int_{0}^{m_p}{dm} = v_e \ m_p \ \textup{[N.s]}](../pages_nanosats/equations_nanosates-comprendre-materiel-propulsion/equation10.png) .
.
Il est essentiel de définir des paramètres permettant de comparer la performance des différents systèmes propulsifs. Le plus utilisé, l'impulsion spécifique (Isp), peut être obtenue expérimentalement. Elle se définit comme l'impulsion délivrée par unité de poids de carburant : 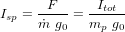 , avec
, avec  le champ standard de la pesanteur (9,81 m.s-2). Les impulsions spécifiques sont notées en secondes et parfois données en N.s.kg-1, ce qui correspond à la formule précédente multipliée par l'accélération standard de la pesanteur, donnant l'impulsion délivrée par unité de masse.
le champ standard de la pesanteur (9,81 m.s-2). Les impulsions spécifiques sont notées en secondes et parfois données en N.s.kg-1, ce qui correspond à la formule précédente multipliée par l'accélération standard de la pesanteur, donnant l'impulsion délivrée par unité de masse.
Dans le but de déterminer la performance du système propulsif dans son ensemble, en incluant la masse de l'ensemble (l'électronique, le carburant et réservoir, l'alimentation) mps, on introduit l'impulsion spécifique du système, notée Issp : ![I_{ssp} = \frac{I_{tot}}{m_{ps} \ g_0} \ \textup{[s]}](../pages_nanosats/equations_nanosates-comprendre-materiel-propulsion/equation13.png) .
.
Action-réaction
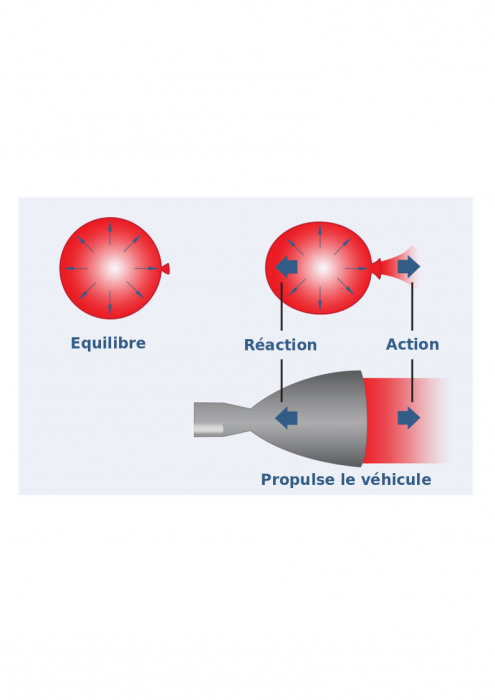
Illustration du principe d'action-réaction. Le carburant éjecté propulse le véhicule dans la direction opposée.
Systèmes de propulsion
Auteur: Gary Quinsac
Systèmes de propulsion
Le sous-système de propulsion est en interaction proche avec les sous-systèmes mécanique et thermique, notamment pour l'implantation des réservoirs et le contrôle thermique de la propulsion. Il doit également respecter les exigences du contrôle d'attitude et d'orbite (SCAO). Si son principe de fonctionnement est basique (une énergie emmagasinée est libérée afin de transmettre une énergie cinétique à un véhicule) il existe différents types de propulsion, eux-mêmes divisés en sous-groupes :
- la propulsion chimique dans laquelle un gaz à haute est libéré avec une importante quantité de mouvement,
- la propulsion électrique qui utilise une énergie électrique ou électromagnétique afin d'augmenter la quantité de mouvement du carburant expulsé,
- la propulsion "sans-carburant" qui, comme son nom l'indique, ne nécessite pas de carburant. Elle ne sera pas détaillée dans ce cours (ex : voile solaire).
Dans le but de répondre aux exigences du SCAO, les systèmes de propulsion sont en particulier caractérisés par :
- une faible poussée avec de faibles niveaux d'accélération,
- des modes d'opération continus pour le contrôle d'orbite,
- des modes d'opération pulsés pour le contrôle d'attitude,
- des performances prédictibles, précises et répétables,
- leur stockage (fiabilité...),
- l'impact des particules émises.
Certains de ces critères sont repris dans le tableau suivant pour les différents types de propulsion introduits dans ce cours.
Comparaison des différents types de propulsion
| Type de propulsion | Fiabilité | Coût | Isp | Poussée | Puissance électrique |
|---|
| Gaz froids | Gaz | Très bonne | Très bas | Très basse | Faible | Très faible |
| Liquide | Bonne | Très bas | Très basse | Faible | Très faible |
| Gaz chauds | Solide | Bonne | Bas | Moyenne | Très forte | Très faible |
| Mono-carburant | Bonne | Bas | Basse | Faible | Très faible |
| Bi-carburant | Moyenne | | Haute | Moyenne | Très faible |
| Électrique | Électrothermique | Moyenne | | Haute | Très faible | Forte |
| Électromagnétique | Faible | | Très haute | Extrêmement faible | Forte |
| Électrostatique | Faible | | Extrêmement haute | Très faible | Très forte |
Une comparaison de la force de poussée et de l'impulsion spécifique de systèmes de propulsion adaptés aux nano.micro-satellites est proposée dans cette figure.
Classification des sous-systèmes de propulsion
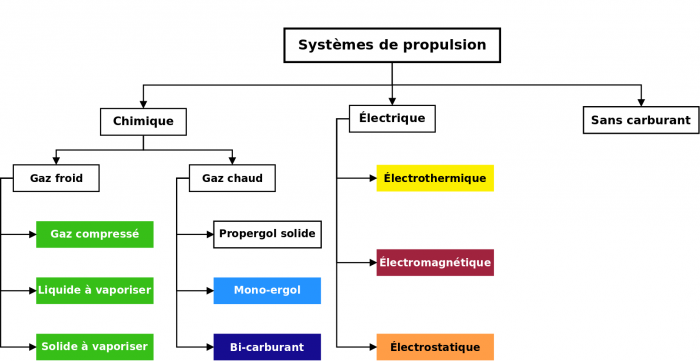
Les principaux systèmes de propulsion sont ici classés par catégorie. Les couleurs indiquées sur cette figure correspondent au couleurs présentes dans la figure suivante.
Crédit :
Gary Quinsac
Performances de systèmes de propulsion pour CubeSat
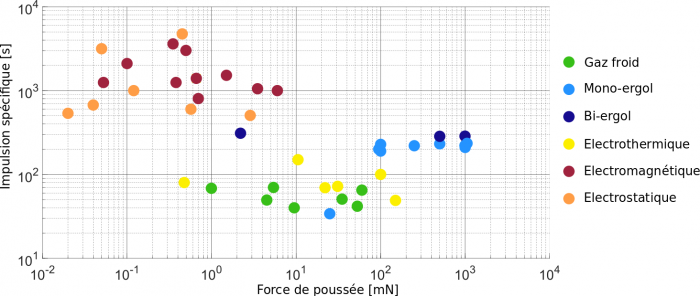
Impulsion spécifique et force de poussée de systèmes de propulsion pour CubeSat (en développement pour la plupart en 2018). Des couleurs permettent de différencier les différents types de propulsion.
Crédit :
Gary Quinsac
Propulsion chimique
La propulsion chimique utilise des gaz à haute température et/ou pression, accélérés à travers une tuyère. Les systèmes de propulsion chimique sont généralement associés à des impulsions spécifiques plus faibles que les propulsions électriques, mais de plus grandes poussées. On peut les diviser en deux catégories : les systèmes à gaz froid et à gaz chaud.
Systèmes de propulsion à gaz froid
Ces systèmes utilisent des gaz stockés sous haute pression ou sous forme liquide. Les gaz sont détendus dans une tuyère convergente-divergente pour obtenir la force de poussée. Ce sont les systèmes les plus simples à mettre en œuvre, mais cela s'accompagne d'une faible force de poussée et d'un faible rendement (impulsion spécifique). Ils présentent une bonne aptitude au fonctionnement en mode pulsé, du fait du faible temps de réponse, les rendant attrayant pour assurer le contrôle d'attitude. Ils ont également l'avantage de limiter les contaminations de l'environnement, ce qui est intéressant notamment pour les optiques des missions scientifiques.
La simplicité de ces systèmes les rend intéressants pour les CubeSats. Néanmoins, du fait de la nécessité de pressuriser le carburant, ils ne respectent pas le cahier des charges décrit par le CDS ("CubeSat Design Specification").
Systèmes de propulsion à gaz chauds
Pour les missions requérant des niveaux de poussée et d'impulsion supérieurs, les gaz froids ne sont plus adaptés et il est nécessaire d'utiliser des carburants plus énergétiques générant des gaz chauds. Les systèmes à gaz chaud sont le type le plus commun de propulsion spatiale. Les ergols des systèmes à gaz chaud sont stockés à l'état liquide ou solide. Une réaction de combustion exothermique de l'ergol est nécessaire pour obtenir des produits à haute température qui sont ensuite expulsés dans la tuyère. Ils nécessitent donc généralement une étape de plus que les gaz froids. On les classe en deux catégories en fonction de leur ergol :
- liquide, comprenant mono-ergol et bi-liquide,
- solide, mais cela concerne les fusées et non les satellites car ils ne sont pas rallumables.
Mono-ergols
Le mono-ergol le plus utilisé est l'hydrazine. Il se décompose dans le propulseur par catalyse. Les gaz chauds résultant sont explulsés par la tuyère. Il présente l'avantage d'être fiable tout en conservant de bonnes performances, mais sa haute toxicité a poussé les chercheurs à s'orienter vers des aternatives appelée "mono-ergols verts". Ces ergols sont des sels dérivés de l'acide nitrique, tels que le dinitramide d'amonium.
Bi-liquides
Dans les systèmes à bi-liquides, deux ergols, un comburant et un carburant, produisent une force de poussée par combustion. Ils sont introduits séparément dans la chambre de combustion où ils s'inflamment spontanément par contact et génèrent des gaz chauds, une nouvelle fois détendus dans la tuyère. Ces systèmes sont plus complexes et plus chers que les systèmes présentés précédemment, mais ils sont également plus efficaces (meilleure Isp) et plus puissants (meilleure poussée).
Schéma des systèmes de propulsion chimiques
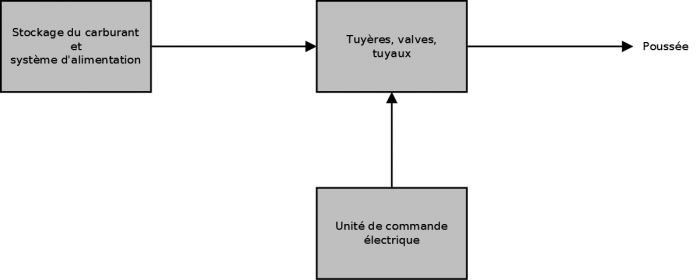
Crédit :
Gary Quinsac
Propulsion électrique
La propulsion électrique contourne la limitation fondamentale de la propulsion chimique, c'est-à-dire que l'énergie du carburant expulsé ne dépend que de son énergie chimique et du débit. Une énergie électrique ou électromagnétique est utilisée afin d'éjecter de la matière à des vitesses beaucoup plus élevées. En d'autres termes, on utilise la puissance électrique issue du sous-système électrique (panneaux solaires, batteries...) pour accélérer le carburant et produire une force de poussée. Ces vitesses d'éjection plus importantes se traduisent immédiatement par une plus grande efficacité (moins de carburant est nécessaire pour obtenir un même incrément de vitesse). Néanmoins, les forces de poussée produites sont nettement plus faibles que dans le cas de la propulsion chimique. Par conséquent, la propulsion électrique est préférée lorsque le ΔV à réaliser est important ou lorsque il est nécessaire des manœuvres avec des poussées très faibles (contrôle d'attitude très précis, etc.).
La propulsion électrique offre une grande gamme de performances en fonction du type de sous-système utilisé. On les classe ainsi en trois catégories : les systèmes électrothermaux, électromagnétiques et électrostatiques.
Systèmes de propulsion électrothermaux
Historiquement, ces systèmes sont une amélioration par rapport aux systèmes de propulsion chimiques. Le gaz est chauffé en passant le long d'une surface chauffée électriquement ou à travers un arc électrique afin de lui conférer plus d'énergie. Le gaz ainsi chauffé bénéficie d'une détente plus efficace.
Systèmes de propulsion électromagnétiques
La propulsion électromagnétique utilise la conversion d'un gaz en plasma. Le plasma est constitué d'électrons (de charge électrique négative), d'ions (pour la plupart de charge électrique positive) et d'atomes ou molécules neutres (non chargés électriquement). Les ions positifs résultants sont alors accélérés à de très grandes vitesses par l'énergie électrique grâce à la force de Laplace  , où
, où 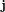 et
et 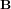 sont respectivement le flux de courant ionique dans le plasma et le champ magnétique. Il en résulte une force de poussée sur le satellite dans la direction opposée.
sont respectivement le flux de courant ionique dans le plasma et le champ magnétique. Il en résulte une force de poussée sur le satellite dans la direction opposée.
Contrairement aux systèmes électrostatiques qui vont être présentés par la suite, les systèmes électromagnétiques expulsent un plasma globalement neutre, ce qui est intéressant pour éviter de charger électriquement le reste du satellite. Cette famille de propulseurs contient notamment les PPT (Pulsed Plasma Thrusters), les VAT (Vacuum Arc Thrusters) ou encore les MPDT (Magneto Plasma Dynamic Thrusters).
Systèmes de propulsion électrostatiques
À la manière de l'accélération électromagnétique, l'énergie électrique est dans un premier temps utilisée pour transformer le fluide propulsif en plasma. La différence se situe au niveau de l'accélération des ions qui n'est plus obtenue par les forces de Laplace mais par l'application d'un champ électrostatique 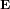 créant une force de Coulomb (
créant une force de Coulomb (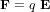 ). Les systèmes de propulsion électrostatiques nécessitent généralement l'installation d'un neutraliseur (cathode) qui fournit des électrons au faisceau d'ions, afin de conserver la neutralité électrique du jet.
). Les systèmes de propulsion électrostatiques nécessitent généralement l'installation d'un neutraliseur (cathode) qui fournit des électrons au faisceau d'ions, afin de conserver la neutralité électrique du jet.
Parmi les propulseurs électrostatiques, on peut citer les propulseurs ioniques, les propulseurs à effet Hall et propulseurs FEEP (Field Emission Electric Propulsion).
Schéma des systèmes de propulsion électriques
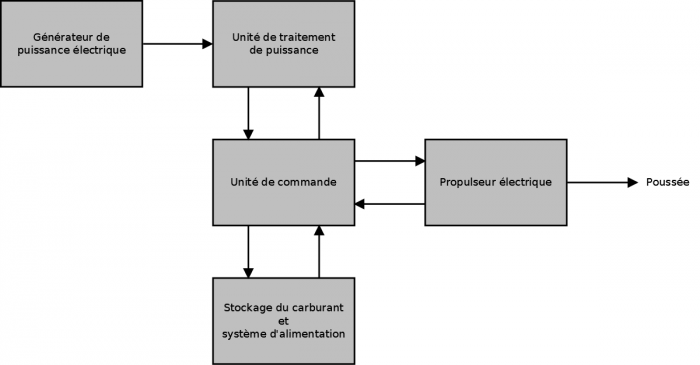
Crédit :
Gary Quinsac
Filtrage et lois de commande
Auteur: Gary Quinsac
Introduction
Le filtrage et les lois de commande sont présentés car ce spaont des aspects essentiels d'un SCAO. Néanmoins, ce cours a simplement pour ambition de vous en faire une brève introduction.
En mathématiques et en ingénierie, la théorie du contrôle a comme objet l’étude du comportement de systèmes dynamiques. En électronique et traitement du signal, un filtre est originellement un circuit qui rejette une partie indésirable d'un signal. On appelle également filtre un outil logiciel dont le but est la séparation des fréquences contenues dans un signal numérisé.
Estimation d'attitude
Auteur: Gary Quinsac
Principe
L'estimation d'attitude consiste à estimer l'état actuel de l'orientation d'un satellite à partir d'un jeu d'observations et de références obtenues à partir de modèles. Ces observations ont été préalablement effectuées par des capteurs fixés sur le satellite. L'objectif est ici de trouver la meilleure estimation de l'état réel du système sous forme de matrice de changement de repère ou de quaternion d'attitude. La résolution exacte du problème n'est généralement pas possible car les observations sont entachées d'erreurs (erreurs de mesure, d'orientation du capteur, de modélisation...). De plus, on dispose souvent d'une surabondance d'information puisque plusieurs capteurs fournissent des informations par rapport à des références différentes (Soleil, champ magnétique, étoile...). On cherche alors à exploiter de manière optimale ces sources d'information en leur associant des modèles d'erreur.
Les problèmes de détermination d'attitude font intervenir des observations (orientation d'objets) pris à certaines dates. La détermination d'attitude statique représente le cas le plus simple, dans lequel on considère que toutes les mesures sont effectuées au même instant. Au contraire, lorsque le temps est introduit, on parle de détermination d'attitude récursive.
La qualité de la connaissance d'attitude dépend des limitations des capteurs, de la quantification des données, du temps d'échantillonnage et du traitement numérique. La détermination d'attitude embarquée est limitée par les capacités de filtrage de l'ordinateur de bord. Il arrive que pour obtenir une meilleure connaissance de l'attitude a posteriori les données des capteurs soient transmises au segment sol où elles sont post-traitées puis exploitables (par le segment sol ou le satellite).
Boucle SCA

Boucle de contrôle d'attitude.
Crédit :
Gary Quinsac
Cas statique
Le cas particulier de l'estimation d'attitude à partir de mesures simultanées de directions non parallèles est ici introduit. À chaque observation sont associés deux vecteurs. Le premier est un vecteur unitaire 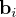 définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire
définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire 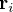 qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale
qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale  satisfaisant pour chaque observation i :
satisfaisant pour chaque observation i :
Méthode TRIAD
La méthode TRIAD se base sur l'observation de deux directions non-parallèles. Il s'agit de déterminer la MCD  permettant de transformer les vecteurs de référence
permettant de transformer les vecteurs de référence 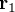 et
et 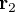 en vecteurs d'observation
en vecteurs d'observation 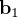 et
et 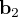 . Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD)
. Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD) 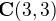 satisfaisant :
satisfaisant :
![\bold y_i = [C] \ \bold x_i](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation11.png) ,
, 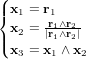 ,
, 
Cette méthode présente l'avantage d'être extrêmement simple, d'où son utilisation dans de nombreuses missions passées. De nos jours, cette méthode n'est plus considérée comme suffisamment précise. En effet, les mesures d'observation sont entachées d'erreur, ce qui empêche d'obtenir le même résultat suivant le vecteur d'observation choisi au départ. C'est pour cette raison que l'on choisit généralement l'observation la plus précise. Des techniques de calcul de la covarience de l'erreur de l'estimation ont été développées pour parer à ces inconvénients.
Méthode QUEST
Un critère quadratique peut être utilisé pour déterminer la matrice d'attitude. Cela revient à chercher la matrice orthogonale  minimisant la fonction de moindres carrés :
minimisant la fonction de moindres carrés :
![L = \frac{1}{2} \ \sum_{i=1}^{n}{a_i \left| \bold b_i - [C] \bold r_i \right|^2}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation15.png)
La minimisation de ce critère n'a rien d'évident et de nombreuses méthodes ont été proposées. Il s'agit d'identifier les 9 paramètres de la MCD respectant les différentes contraintes énoncées précédemment (moindres carrés et règles de la MCD). L'algorithme QUEST (QUaternion ESTimation) offre une alternative intéressante. La forme quadratique est alors utilisée à la place de la MCD, permettant de réduire le nombre de paramètres. Nous ne rentrerons pas dans le détail de cette méthode dans le cadre de ce cours.
Cas général
Dans le cas général où nous ne disposons pas de plusieurs mesures de directions non parallèles effectuées au même instant, le problème d'estimation devient dépendant du temps. Bien que des méthodes récursives basées sur l'algorithme QUEST aient été développées et utilisées, le filtrage de Kalman est le moyen le plus utilisé pour estimer l'attitude d'un satellite en présence de bruits de mesure.
Filtre de Kalman
Le filtre de Kalman a été développé en 1960 comme une nouvelle approche pour le filtrage linéaire et les problèmes de prédiction. Il permet de maintenir une estimation de l'état d'un système dynamique en dehors des périodes d'observation, à partir d'un modèle de son erreur. Puisqu'il s'agit d'un filtre récursif, la quantité d'informations à traiter reste limitée, ce qui en fait un filtre très apprécié à bord des satellites. On a pour habitude de distinguer deux phases dans ce type de filtres, la prédiction et la mise à jour :
- la phase de prédiction intervient lorsqu'aucune observation n'est disponible ; le filtre se base sur le modèle dynamique embarqué pour mettre à jour les paramètres estimés, tout en mettant à jour la matrice de covariance de l'erreur d'estimation ; cette dernière augmente durant cette phase en raison de l'incertitude inhérente au modèle dynamique,
- la mise à jour intervient lorsqu'une observation est disponible ; il devient alors possible de comparer la prédiction à l'observation ; les prédictions sont ainsi mises à jour, en tenant compte des incertitudes liées à l'observation et à la prédiction. Si les incertitudes liées aux observations sont plus faibles que celle du modèle alors cette phase fait décroître la covariance.
 Filtre de Kalman discret
Filtre de Kalman discret
C'est la version la plus simple du filtre de Kalman, seules l'estimation de l'état précédent et les mesures actuelles sont nécessaires.
Phase de prédiction
Durant la phase de prédiction, l'état et l'estimation de la covariance sont projetés dans le temps de l'état k-1 à l'état k :
![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation29.png) est la matrice de covariance du bruit de processus
est la matrice de covariance du bruit de processus  ,
, ![[P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation31.png) est la matrice d'estimation a priori de la covariance de l'erreur.
est la matrice d'estimation a priori de la covariance de l'erreur.
À chaque étape le processus est répété afin d'obtenir de nouvelles estimations a posteriori à partir des estimations a priori. En pratique, la matrice de covariance ![[R]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation42.png) du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus
du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus ![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation43.png) car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
La plupart des systèmes physiques, et notamment ceux étudiés, sont non linéaires. Le filtre de Kalman classique n'est donc optimal que sur une faible portion des phénomènes pris en compte. Dans le cas de systèmes non-linéaires, nous utilisons donc un filtre de Kalman étendu, ou "Extended Kalman Filter".
Lois de contrôle
Auteur: Gary Quinsac
Introduction à la théorie du contrôle
La théorie du contrôle s'intéresse au comportement de systèmes dynamiques en fonction de leurs paramètres. Elle peut être vue comme une stratégie permettant de sélectionner la bonne entrée d'un système pour que le sortie soit celle désirée. Cela fait partie du domaine de l'automatique.
Boucles ouvertes et fermées
Un système de contrôle est un mécanisme altérant l'état futur d'un système. En l'absence de retour d'information concernant la sortie du système, on se trouve dans le cas d'une boucle ouverte. Prenons l'exemple d'un lave-vaisselle. Celui-ci est programmé pour tourner un certain temps, à une certaine température et avec une certaine quantité d'eau. Ces paramètres ne dépendent pas de l'état de la vaisselle qu'il contient.
Une boucle de rétroaction peut être ajoutée afin de modifier intelligemment la durée du cycle. On obtient alors ce que l'on appelle une boucle fermée, puisqu'une information sur l'état de sortie de notre système, obtenue à l'aide de capteurs, va être comparée à un signal de référence afin de nourir un contrôleur qui a la charge de choisir la bonne entrée. On peut ici parler d'asservissement.
Les boucles de contrôle d'attitude ont pour but d'assurer un contrôle stable de l'orientation du satellite, en prenant en compte les contraintes opérationnelles (temps de réponse aux commandes par exemple) et les perturbations externes et internes. On met en place un asservissement dans le but d'atteindre une valeur de consigne et de la maintenir. Pour ce faire, l'asservissement, ou correcteur, mesure en permanence l'écart entre la valeur réelle de la grandeur à asservir et la valeur de consigne. Il en déduit la commande appropriée que les actionneurs devront ensuite appliquer afin de réduire cet écart.
Systèmes linéaires
Un système linéaire est un objet qui peut être décrit par des équations linéaires. De tels systèmes sont essentiels car nous pouvons les résoudre. Pourtant, presque aucun système réel n'est un système linéaire. L'objectif est donc de simplifier l'objet étudié (actionneur, capteur, système dynamique...) afin de pouvoir l'approximer par un système linéaire. On parle alors de son domaine linéarité.
La réponse d'un système linéaire peut être obtenue en sommant ses réponses impulsionnelles. Cette sommation dans le domaine temporel est appelée convolution. Soit un signal d'entrée u(t) et une réponse impulsionnelle g(t), la sortie y(t) s'exprime :
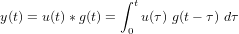
Représentation de la boucle de contrôle d'attitude
On représente la boucle du SCA comme un contrôle en boucle fermée, avec le terme de rétroaction. On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, Gc(p) le contrôleur, E(p) l'erreur, Gp(p) le matériel à contrôler et C(p) la dynamique des capteurs. Si l'on considère que les perturbations sont nulles, la fonction de transfert s'écrit :
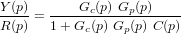
Le dénominateur de cette équation est un polynome dont les racines déterminent le type de réponse. Le contrôleur peut être utilisé pour stabiliser le système ou lui donner des caractéristiques particulières.
Boucle ouverte ou fermée
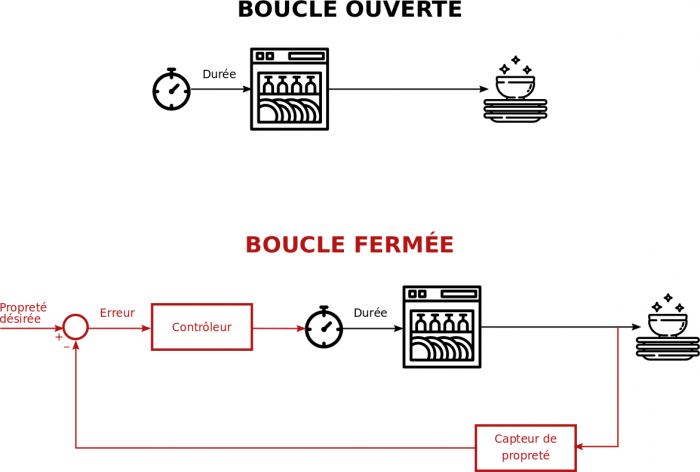
Dans la boucle ouverte, la durée du cycle de lavage ne dépend pas de la propreté de la vaisselle qu'il contient. Afin d'adapter cette durée à l'état des assiettes et verres, il faut qu'un capteur de propreté fournisse une information à comparer à la propretée désirée et qu'un contrôleur en déduise une nouvelle durée. C'est ce que l'on appelle une boucle fermée.
Crédit :
Gary Quinsac
Fonction de transfert
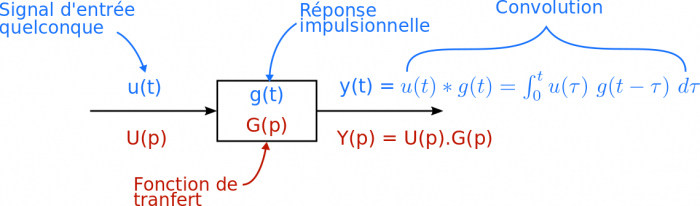
Crédit :
Gary Quinsac
Diagramme en bloc de la boucle de contrôle
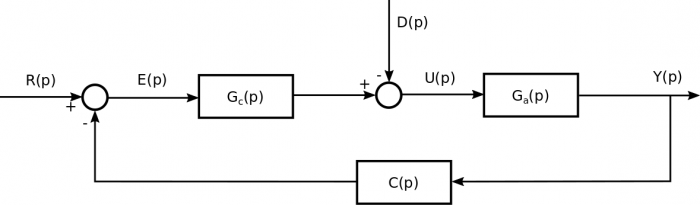
Chaque élément de la boucle de contrôle d'attitude est représenté par sa fonction de transfert.
Crédit :
"Fundamentals of Spacecraft Attitude Determination and Control", F. Landis Markley et John L. Crassidis.
Contrôleur
Le contrôleur a pour objectif de convertir l'erreur, c'est-à-dire l'écart entre la mesure de la sortie de la boucle et le signal de référence, en un signal de contrôle qui va finir par ramener l'erreur à 0.
Les performances du contrôleur et a fortiori de l'asservissement sont décrites par plusieurs paramètres :
- la rapidité, qui définit la vitesse à laquelle une valeur de sortie stable est atteinte; la rapidité est caractérisée par le temps de réponse du système ;
- la stabilité, qui définit la capacité de l'asservissement à produire une sortie tendant vers une valeur finie pour une entrée constante (pas d'oscillation ou de divergence) ;
- le dépassement de la consigne, qui correspond au dépassement par la sortie de la valeur de consigne avant de se stabiliser ;
- la précision, c'est-à-dire la capacité de l'asservissement à atteindre la consigne avec précision le plus rapidement possible.
L'asservissement doit ainsi assurer un compromis entre performance et stabilité. La performance est proportionnelle à la valeur du gain du correcteur, mais à partir d'une certaine valeur celui-ci a tendance à déstabiliser le système.
Facteur d'amortissement
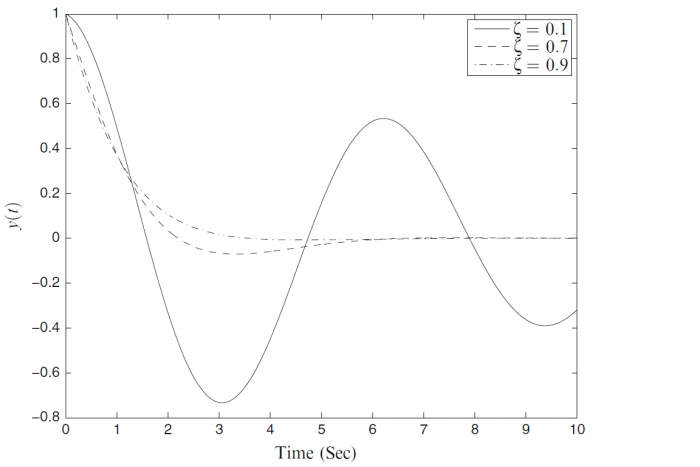
Réponse pour différents facteurs d'amortissement.
Crédit :
"Fundamentals of Spacecraft Attitude Determination and Control", F. Landis Markley et John L. Crassidis.
Se tester
Auteur: Gary Quinsac
Présentation des exercices
Cette section doit vous permettre de vous exercer sur certaines des notions présentées dans ce cours. Un QCM reprend la première partie du cours, soit la découverte d'une mission spatiale, du standard CubeSat et du système de contrôle d'attitude et d'orbite. Des exercices plus poussés sont ensuite proposés, recouvrant la représentation d'attitude, les équations du mouvement, les couples perturbateurs et le contrôle d'attitude, la propulsion et enfin les lois de commande. La majeure partie des aspects abordés dans ce cours trouvent ainsi un écho dans ces exercices.
QCM sur la partie "découvrir"
Exercices : Représentation d'attitude
Auteur: Gary Quinsac
 Matrice du Cosinus Directeur
Matrice du Cosinus Directeur
Difficulté : ☆
On souhaite montrer que la MCD est une matrice orthonormale, c'est-à-dire que ![[T] \ [T]^T = [I] = [T]^T \ [T]](../pages_nanosats/equations_nanosats-setester/equation1.png) .
.
Soit la MCD ![[T]_{B|A}](../pages_nanosats/equations_nanosats-setester/equation2.png) entre deux référentiels orthogonaux décrits par les vecteurs unitaires
entre deux référentiels orthogonaux décrits par les vecteurs unitaires  et
et 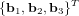 :
:
![\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = [T]_{B|A} \ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation5.png)
Question 1)
Ecrire le vecteur transposé de 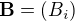 .
.
Question 2)
Calculer le produit 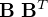 et conclure.
et conclure.
Auteur: Gary Quinsac
 Angles d'Euler
Angles d'Euler
Difficulté : ☆
Cet exercice a pour but de démontrer l'expression de la MCD à partir d'une certaine séquence d'angles d'Euler. On reprend la notation du cours en nommant 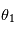 ,
, 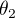 et
et 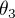 les trois angles d'Euler.
les trois angles d'Euler.
Question 1)
Démontrer qu'en choisissant la séquence ![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation15.png) afin de passer du référentiel
afin de passer du référentiel 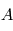 au référentiel
au référentiel 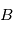 , on obtient bien la formule présentée dans le cours :
, on obtient bien la formule présentée dans le cours :
![[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation18.png)
Exprimer les trois rotations élémentaires telles que présentées dans le cours.
Exprimer la matrice issue de la combinaison des rotations suivantes :
![\begin{cases} \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} = [T(\theta_3)]_3 \ \begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} \\ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} = [T(\theta_2)]_2 \ \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} \\ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} = [T(\theta_1)]_1 \ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} \end{cases}](../pages_nanosats/equations_nanosats-setester/equation19.png)
Question 2)
Considérons maintenant la séquence suivante : ![[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2](../pages_nanosats/equations_nanosats-setester/equation20.png) . Exprimer la MCD associée à cette séquence.
. Exprimer la MCD associée à cette séquence.
Suivre les mêmes étapes que pour la question précédente.
Auteur: Gary Quinsac inspiré de "Space Vehicle Dynamics and Control" de Bong Wie.
 Quaternions
Quaternions
Difficulté : ☆
Considérons la séquence de rotations fixées par rapport à un satellite allant du référentiel 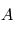 au référentiel
au référentiel 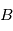 :
:
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation24.png)
Les quaternions associés à ces rotations sont :
![[T(\theta_1)]_1 = \begin{pmatrix} sin(\theta_1 / 2) \\ 0 \\ 0 \\ cos(\theta_1 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation25.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ sin(\theta_2 / 2) \\ 0 \\ cos(\theta_2 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation26.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ 0 \\ sin(\theta_3 / 2) \\ cos(\theta_3 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation27.png)
Question 1)
Montrer que les angles d'Euler de cette séquence de rotation sont reliés aux quaternions de la manière suivante :
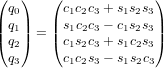
où 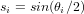 et
et 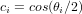
Utiliser le cours sur les séquences de rotations exprimées en termes de quaternion et la multiplication des quaternions.
Question 2)
Vérifier que pour des angles infinitésimaux on obtient un quaternion très simple.
Effectuer le développement limité de du quaternion obtenu précédemment.
Exercices : Equations du mouvement
Auteur: Gary Quinsac
 Cinématique d'attitude avec la MCD
Cinématique d'attitude avec la MCD
Difficulté : ☆☆
On souhaite démontrer l'équation de la cinématique exprimée avec la MCD.
![\frac{d}{dt}([T]) = -[\Omega] \ [T]](../pages_nanosats/equations_nanosats-setester/equation32.png) avec
avec ![[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation33.png) et
et ![[T] = \begin{pmatrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation34.png)
Soit la MCD ![[T]](../pages_nanosats/equations_nanosats-setester/equation35.png) entre deux référentiels orthogonaux décrits par les vecteurs unitaires
entre deux référentiels orthogonaux décrits par les vecteurs unitaires 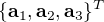 et
et 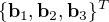 .
.
Question 1)
Rappeler la propriété principale de la MCD ![[T]](../pages_nanosats/equations_nanosats-setester/equation38.png) .
.
Voir le cours où l'exercice sur la représentation d'attitude avec la MCD.
Question 2)
Exprimer la dérivée de l'équation exprimant un vecteur du référentiel (B) en fonction d'un vecteur du référentiel (A).
Exprimer la relation de passage du vecteur 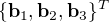 au vecteur
au vecteur 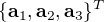 .
.
![\begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} = [T]^T \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation42.png)
Prendre la dérivée de l'équation précédente.
Question 3)
Obtenir l'équation de la cinématique exprimée avec la MCD.
Remplacer par la matrice antisymétrique :
![[\Omega] = \begin{pmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation48.png)
Question 4)
À partir de l'équation de la cinématique que nous venons de démontrer, exprimer les différentes coordonnées du vecteur vitesse angulaire.
Il s'exprime en fonction des différents éléments de la MCD et de sa dérivée.
Auteur: Gary Quinsac
 Cinématique d'attitude avec les angles d'Euler
Cinématique d'attitude avec les angles d'Euler
Difficulté : ☆☆
Cet exercice cherche à établir les équations de la cinématique pour certaines représentations d'Euler. Les premières questions considèrent la séquence d'Euler permettant de passer du référentiel (A) au référentiel (B) suivante :![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation52.png) .
.
Question 1)
Ecrire les trois vecteurs vitesse angulaire correspondant à chaque transformation élémentaire en fonction des dérivées des angles d'Euler.
Penser à introduire les référentiels intermédiaires.
Question 2)
Exprimer le vecteur de vitesse angulaire 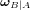 en fonction des vecteurs de vitesse angulaire précédents.
en fonction des vecteurs de vitesse angulaire précédents.
Question 3)
Reformuler cette équation afin de faire apparaître les vecteurs de base des différents repères.
Question 4)
Exprimer les vecteurs de base des repères 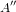 et
et 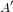 en fonction de ceux de (B).
en fonction de ceux de (B).
Question 5)
Montrer la relation de la cinématique pour cette séquence d'Euler :
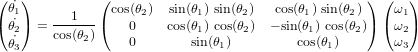
Question 6)
Considérons maintenant la séquence suivante : ![[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2](../pages_nanosats/equations_nanosats-setester/equation62.png) . Exprimer alors l'équation de la cinématique.
. Exprimer alors l'équation de la cinématique.
Suivez les mêmes étapes que pour la question précédente.
Auteur: Gary Quinsac
 Cinématique d'attitude avec les quaternions
Cinématique d'attitude avec les quaternions
Difficulté : ☆☆
Il est maintenant question de démontrer l'équation de la cinématique avec les quaternions.
Question 1)
Reprendre la forme de l'équation de la cinématique trouvée dans la dernière question du premier exercice sur les équations du mouvement :
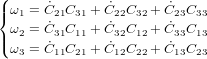
Substituer les coefficients de la MCD par leur forme avec les quaternons.
Question 3)
Regrouper ces 4 équations sous forme matricielle.
Question 4)
Utiliser une propriété remarquable de la matrice de quaternion obtenue dans la questions précédente pour exprimer la dérivée du quaternion.
La matrice de quaternion obtenue est orthonormale.
Question 5)
Réécrire l'équation afin d'obtenir l'équation de la cinématique avec les quaternions.
Exercice : Couples perturbateurs sur un CubeSat
Auteur: Gary Quinsac
 Couples perturbateurs agissant sur un CubeSat
Couples perturbateurs agissant sur un CubeSat
Difficulté : ☆☆
Une mission scientifique nécessite l'envoie d'un CubeSat 3U sur une orbite circulaire à 300km d'altitude (ce qui correspond à une vitesse de 7726 m/s). On considère que le centre de masse de satellite se trouve décalé du centre géométrique de + [1; 1; 2] cm et que la surface du satellite est homogène. Étant donnée l'altitude, il est possible d'utiliser le champ magnétique pour effectuer le contrôle de l'attitude du CubeSat. Une combinaison de trois magnétocoupleurs, chacun étant orienté selon un axe du satellite, est proposée. Le courant maximum parcourant les bobines est ±0,2 A et le rayon du fil mesure 10,4 mm.
Voici différentes données nécessaires :
Données
| Masse volumique de l'atmosphère à 300 km |  |
| Coefficient de trainée |  |
| Constante gravitationnelle de la Terre | 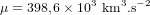 |
| Rayon de la Terre | 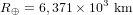 |
| Irradiance solaire moyenne | 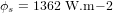 |
| Coefficient de réflexion moyen du satellite | 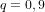 |
| Champ magnétique terrestre à 300 km | 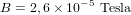 |
| Dipôle résiduel du satellite | 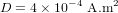 |
| Courant maximum dans magnéto-coupleurs | 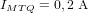 |
| Diamètre de la bobine des magnéto-coupleurs | 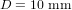 |
CubeSat 3U
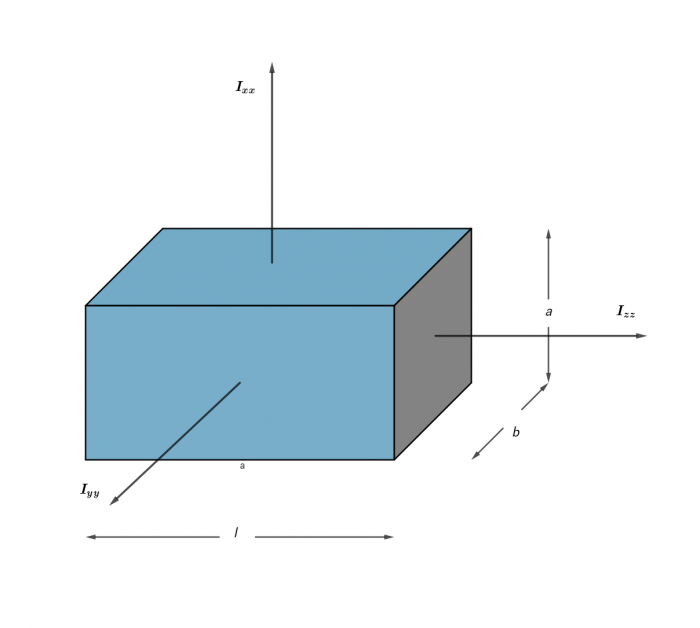
CubeSat 3U de longueur l, de côtés a et b et de moments d'inertie Ixx, Iyy et Izz.
Crédit :
Gary Quinsac
Question 1)
Que signifie le fait que la surface du satellite est homogène ?
Question 2)
Estimer les dimensions et la masse totale du satellite.
C'est un CubeSat 3U et on sait qu'une unité représente un cube de 10 cm d'arête et de 1,3 kg.
Question 3)
Quels sont les principaux moments d'inertie du satellite ?
Comme première approximation, on peut considérer que le satellite est homogène et que son centre de masse se trouve parfaitement localisé en son centre. Les moments d'inertie principaux peuvent donc s'exprimer :
Question 4)
Identifier les couples perturbateurs.
Question 5)
Exprimer les couples perturbateurs maximums créés par les différentes perturbations agissant sur le satellite si son axe +Y est aligné avec sa vitesse. On utilisera les notations données en introduction de l'exercice.
Pour la trainée atmosphérique :
- Déterminer l'aire projetée le long de la direction du mouvement.
- Exprimer la force de trainée atmosphérique :
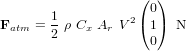
- Utiliser la position du centre de masse pour calculer les couples de trainée atmosphérique selon les trois axes principaux du satellite :
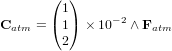
Pour le gradient magnétique :
- Identifier le pire alignement entre le satellite et le champ magnétique terrestre : lorsque le dipôle résiduel et le champ magnétique sont perpendiculaires.
- Le couple correspondant est simplement le produit de ces deux valeurs :
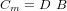
Question 6)
Estimer l'ordre de grandeur de la somme de tous les couples perturbateurs agissant sur le satellite.
Question 7)
Combien de spires la bobine du magnétocoupleur doit-elle contenir pour contrebalancer le couple perturbateur précédemment estimé ?
Les magnéto-coupleurs doivent pouvoir compenser tous les couples perturbateurs agissant sur le satellite. Ils doivent donc au moins fournir 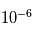 N.m.
N.m.
Rappelons les équations permettant de calculer le couple magnétique et le moment dipolaire :
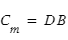 et
et 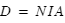 , où N est le nombre de spire de la bobine.
, où N est le nombre de spire de la bobine.
Exercice : Propulsion
Auteur: Gary Quinsac
 Exercice
Exercice
Difficulté : ☆
On reprend le CubeSat présenté lors de l'exercice précédent. Cette fois-ci, nous nous plaçons dans le cas où celui-ci doit effectuer une manœuvre orbitale nécessitant un incrément de vitesse de 50 m/s. Six systèmes de propulsion vous sont proposés, chacun étant défini par sa masse sèche Msèche (masse du système de propulsion sans le carburant), son impulsion spécifique Isp, sa force de poussée F et sa consommation électrique P.
Systèmes de propulsion
| Type de propulsion | Modèle | Msèche [kg] | Isp [s] | F [N] | P [W] |
|---|
| Gaz froid | Palomar MiPS | 0,89 | 50 | 3,5.10-2 | 5 |
| Mono-carburant | BGT-X5 | 1,24 | 220 | 5.10-1 | 20 |
| Bi-carburant | PM200 | 1,10 | 285 | 5.10-1 | 6 |
| Électromagnétique | PPTCUP | 0,28 | 670 | 4.10-5 | 2 |
| Électrostatique | IFM Nano | 0,64 | 3800 | 3,5.10-4 | 32 |
Question 1)
Quel lien peut-on faire entre la vitesse d'expulsion du carburant l'impulsion spécifique Isp ?
Cette relation s'obtient facilement à partir de la relation exprimant la force en fonction de la vitesse d'expulsion et la définition de l'impulsion spécifique.
Question 2)
Estimer la quantité de carburant nécessaire pour effectuer la manœuvre souhaitée avec chacun des systèmes de propulsion.
Le CubeSat faisant 3 unités, on peut estimer que sa masse totale est de 4 kg.
Question 3)
Sachant que l'on cherche généralement à éviter d'allouer plus de 33% de la masse d'un satellite au système de propulsion
Il faut sommer la masse de carburant et la masse sèche afin d'obtenir la masse du système de propulsion dans son ensemble. Ceci n'est qu'une première approximation, notamment car on ne prend pas en compte la masse supplémentaire correspondant à des réservoirs plus gros.
Question 4)
La puissance électrique disponible à bord d'un CubeSat 3U recouvert de panneaux solaires en orbite autour de la Terre est estimée à 7 W. Qu'est-ce que cela change au niveau de vos choix ?
Question 5)
En supposant que l'efficacité de la manœuvre ne dépend pas du lieu où celle-ci est effectuée, c'est à dire du moment, combien durerait-elle pour chacun des systèmes de propulsion proposés ? Cette hypothèse est fausse dans de nombreux cas, notamment lorsque les forces de poussée en jeu sont faibles et les manœuvres importantes (ce qui est le cas ici).
Dans ce cas, la durée de la manœuvre est directement liée à la force de poussée.
Exercices : Lois de commande
Auteur: Gary Quinsac
 Étude d'un ressort
Étude d'un ressort
Difficulté : ☆
Cet exercice a pour but de vous entraîner à utiliser les transformations de Laplace pour résoudre une équation différentielle.
Considérons une masse m accrochée à un ressort de constante de rappel K. On mesure le déplacement vertical de la masse, provoqué par une stimulation u(t), par la grandeur x. L'installation est illustrée par cette figure.
Ressort
Crédit :
Gary Quinsac
Question 1)
Quelle est l'équation de déplacement de la masse ?
Question 2)
On veut étudier le cas d'une stimulation impulsionnelle. Que devient u(t) ?
Question 3)
Exprimer la fonction de transfert du système.
Il faut prendre la transformée de Laplace de l'équation exprimée précédemment.
Les conditions initiale sont supposées nulles.
Question 4)
Effectuer la transformée de Laplace inverse de la fonction de transfert afin d'exprimer le déplacement issu d'une stimulation impulsionnelle dans le domaine temporel.
Question 5)
Supposons maintenant que la stimulation n'est plus impulsionnelle mais une rampe 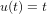 . Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :
. Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :
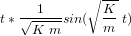
Passer par la transformée de Foutier.
C'est une simple multiplication.
Auteur: Gary Quinsac
 Représentation de la boucle de contrôle d'attitude
Représentation de la boucle de contrôle d'attitude
Nous allons retrouver la fonction de transfert de la boucle de contrôle d'attitude :
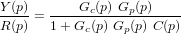
On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, Gc(p) le contrôleur, E(p) l'erreur, Gp(p) le matériel à contrôler et C(p) la dynamique des capteurs.
Question 1)
Exprimer le signal de sortie en fonction du signal de contrôle.
Question 2)
Sachant que l'on considère que les perturbations sont nulles, exprimer le signal de contrôle en fonction de l'erreur.
Question 3)
Appliquer la même approche pour trouver l'expression de l'erreur.
Question 4)
Réorganiser les résultats précédents afin de retrouver l'expression de la fonction de transfert.
Mini-projets
Auteur: Gary Quinsac
Présentation des mini-projets
 Objectifs des mini-projets
Objectifs des mini-projets
Quatre mini-projets vous sont proposés afin de tester vos connaissances. Si certaines informations utiles peuvent être retrouvées dans le cours, il sera également nécessaire d'aller en chercher en dehors. Une liste de questions commune aux différents mini-projets vous est proposée, tâchez d'y répondre pour chacun des cas présentés. Ce cours n'étant qu'une introduction aux nanosatellites et au contrôle d'attitude et d'orbite, les questions sont avant tout qualitatives. De plus, face à la complexité d'une mission spatiale, une approche plus poussée nécessiterait de répondre à ces questions plusieurs fois, de manière itérative, afin de prendre en compte l'impact de chaque décision sur les choix effectués précédemment.
Le travail d'un ingénieur spatial est de développer une mission capable de répondre à des besoins. Dans notre cas, ces besoins sont spécifiés par des chercheurs. Quatre missions nous ont ainsi été proposées. Nous intervenons au tout début de ces projets puisque nous sommes chargés d'étudier leur faisabilité.
Étude de l'ionosphère terrestre
Il nous est demandé d'étudier l'ionosphère terrestre. L'ionosphère représente l'atmosphère supérieure d'une planète, de 85 à 600 km d'altitude, une région où le gaz est partiellement ionisé par les radiations solaires. Son fonctionnement est important car elle constitue la partie intérieure de la magnétosphère de notre planètre. Elle joue notamment un rôle essentiel dans les télécommunications et la géolocalisation par satellite, puisqu'elle a tendance à retarder voire même réfléchir certains signaux. Si de nombreux satellites ont déjà acquis des données sur ce milieu, son étude est plus que jamais d'actualité.
Afin d'effectuer des mesures du contenu de l'ionosphère terrestre, il nous est demandé d'utiliser une sonde de Langmuir. C'est un appareil capable de mesurer la température électronique, la densité électronique ainsi que le potentiel électrique du plasma. Une telle sonde permet d'étudier le plasma in-situ, c'est-à-dire à l'endroit où elle se trouve.
Démonstration technologique d'une nouvelle optique de télescope.
Une équipe de chercheurs est en train de développer une nouvelle optique permettant d'améliorer grandement la performance des télescopes d'observation de la Terre en orbite basse. Afin de qualifier en vol leur système, dernière étape de leur développement, ils souhaitent l'embarquer sur un CubeSat. L'ensemble du télescope avec son électronique de lecture doit faire 1,5 U de volume. La lecture se fait avec un capteur CMOS.
Observation d'un transit d'exo-planète
Suite à la première tentative initiée par la mission PICSAT de l'Observatoire de Paris, des scientifiques veulent observer un nouveau transit d'exoplanète. L'étoile autour de laquelle orbite cette exoplanète se trouve dans le plan de notre galaxie. Le même instrument scientifique que celui embarqué par Picsat est envisagé. Son utilisation permet d'effectuer la photométrie du transit, c'est-à-dire de mesurer la luminosité de l'étoile brillante.
Géodésie d'un astéroïde
Surfant sur la recrudescence de missions d'étude d'astéroïdes, un chercheur nous propose une mission d'accompagnement avec un CubeSat. La mission principale doit étudier le système d'astéroïdes géocroiseur nommé 65803 Didymos. Un CubeSat présente l'intérêt de pouvoir s'approcher beaucoup plus proche du système d'astéroïde (faibles risques associés à son faible coût). Les perturbations provoquées par les astéroïdes lors des survols doit permettre d'en déduire leur champ gravitationnel. Pour ce faire, une mesure précise de l'orbite du satellite est nécessaire. De l'astronomie radio-science est envisagée pour réaliser la mesure précise de la position du CubeSat au cours des survols.
Le CubeSat permet d'étudier les populations d'astéroïde (masse, composition...) et en particulier les nombreux astéroïdes doubles pourtant complexes à examiner. L'enjeu est de comprendre leur origine et leur contribution dans la formation du système solaire. D'une manière plus générale, cette étude doit également permettre d'identifier les lois régissant la formation des systèmes exo-planétaires. C'est cette technique qui a permis d'obtenir la majorité des informations concernant la structure interne des corps du système solaire.
L'utilisation d'un transpondeur similaire à ceux utilisés pour la télécommunication nous offre le suivi du CubeSat depuis le sol ou un autre satellite en effectuant des mesures d'effet Doppler et de distance. Ces mesures permettent d'obtenir la vitesse radiale et la distance entre le CubeSat et l'observateur, permettant de calculer son accélération et de déduire in fine le champ gravitationnel de l'astéroïde. Afin d'obtenir des mesures suffisamment précises, le transpondeur Iris, développé par le JPL, est proposé. Cela veut dire que le suivi peut se faire depuis la mission principale ou depuis le sol avec un réseau d'antennes tel que le Deep Space Network ou le ESA Tracking Network..
 Quelques sources d'information
Quelques sources d'information
Sonde de Langmuir sur le satellite Demeter

On peut voir une sonde de Langmuir embarquée par le satellite Demeter.
Crédit :
CNRS
Télescope d'observation de la Terre

Télescope hyperspectral d'observation de la Terre EnMAP.
Crédit :
DLR
Transit de Vénus

Photographie pris lors du dernier transit de Vénus devant le Soleil en 2012.
Crédit :
ESA
Mission AIDA

Vue d'artiste de la mission AIDA accompagnée d'un CubeSat autour du système d'astéroïdes Didymos. AIDA observe l'impact de la mission DART sur l'astéroïde principal.
Crédit :
ESA/Science Office
Questions
Voici une liste de questions auxquelles vous devez essayer de répondre, en le justifiant, pour les quatre missions qui vous ont été proposées.
I - Considérations générales
- Étant donné le principe de fonctionnement de l'instrument que nous devons embarquer, quel type de mission envisagez-vous (orbite, nombre de CubeSats...) ?
- Qu'est-ce que cela implique concernant le lancement ?
- Que pensez-vous des besoins de télécommunication ?
- La gestion d'énergie sera-t-elle un aspect critique de cette mission ?
- Quel format de CubeSat proposez-vous ?
II - Focalisation sur le SCAO
- Que pouvez-vous dire des effets environnementaux sur le contrôle d'attitude ?
- Quels besoins identifiez-vous en termes de contrôle d'attitude ?
- Ces besoins nécéssitent-ils un contrôle fin de l'attitude des satellites ?
- Quels capteurs et actionneurs recommandez-vous ?
- Sera-t-il nécessaire d'effectuer des manœuvres orbitales ?
- Si oui, évaluez ce que cela représente en budget ΔV.
- Quel type de propulsion vous semble le plus adapté ?
Réponses aux QCM
pages_nanosats-setester/qcm-partie-decouvrir.html
QCM
'Découvrir'
- Question 1
Aide :
Acronyme anglais.
Solution : réponse 3)
(
C'est une orbite basse ou "Low Earth Orbit"
)
- Question 2
Aide :
Les satellites sont habituellement classés en fonction de leur masse.
Solution : réponse 2)
(
Cette catégorie concerne les satellites de 1 kg à 10 kg. Jusqu'à 6U un CubeSat doit peser moins de 10 kg.
)
- Question 3
Aide :
La construction intervient tardivement dans les phases de réalisation d'un projet spatial.
Solution : réponse 5)
(
La construction et les tests ont lieu lors de cette phase.
)
- Question 4
Aide :
Tous ces avantages découlent de la standardisation des interfaces.
Solution : réponse 1)
(
De nombreux sous-système "sur étagère" existant, il n'est plus nécessaire de développer entièrement son satellite.
)
Solution : réponse 3)
(
Il a permis le développement de déployeurs standardisés qualifiés pour bon nombre de lanceurs.
)
- Question 5
Aide :
Le segment spatial se constitue de la plateforme et de la charge utile.
Solution : réponse 1)
(
Elle sert à échanger des données avec le sol.
)
Solution : réponse 2)
(
Vous devez avoir une idée assez précise de son utilité après ce cours.
)
Solution : réponse 4)
(
Elle assure, notamment, l'intégrité du satellite.
)
- Question 6
Aide :
Cette absoprtion par l'atmosphère est l'une des raisons d'être des premiers observatoires spatiaux.
Solution : réponse 1)
(
Heureusement pour nous !
)
Solution : réponse 3)
- Question 7
Solution : réponse 3)
- Question 8
Solution : réponse 1)
(
L'importance croissance des CubeSats commerciaux symbolise l'adoption de ce standard et encourage les nouveaux investisseurs.
)
- Question 9
Aide :
Le contrôle d'attitude concerne l'orientation du satellite dans l'espace.
Solution : réponse 2)
- Question 10
Solution : réponse 3)
(
C'est le système de guidage, navigation et contrôle.
)
Réponses aux exercices
pages_nanosats/exercice-representation-attitude.html
Exercice
'Angles d'Euler'
- Question 1
Aide :
Exprimer les trois rotations élémentaires telles que présentées dans le cours.
Aide :
Exprimer la matrice issue de la combinaison des rotations suivantes :
![\begin{cases} \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} = [T(\theta_3)]_3 \ \begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} \\ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} = [T(\theta_2)]_2 \ \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} \\ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} = [T(\theta_1)]_1 \ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} \end{cases}](../pages_nanosats/equations_nanosats-setester/equation19.png)
- Question 2
Aide :
Suivre les mêmes étapes que pour la question précédente.
pages_nanosats/exercice-representation-attitude.html
Exercice
'Quaternions'
pages_nanosats/exercice-equations-mouvement.html
Exercice
'Cinématique d'attitude avec la MCD'
- Question 1
Aide :
Voir le cours où l'exercice sur la représentation d'attitude avec la MCD.
- Question 2
Aide :
Exprimer la relation de passage du vecteur 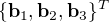 au vecteur
au vecteur 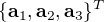 .
.
![\begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} = [T]^T \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation42.png)
Aide :
Prendre la dérivée de l'équation précédente.
- Question 3
Aide :
Exprimer le vecteur de vitesse angulaire de  par rapport à
par rapport à 
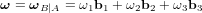 et l'insérer dans l'équation précédente.
et l'insérer dans l'équation précédente.
![\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \dot {[T]}^T \ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} + [T]^T \ \begin{pmatrix} \boldsymbol\omega \wedge \bold b_1 \\ \boldsymbol\omega \wedge \bold b_2 \\ \boldsymbol\omega \wedge \bold b_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation47.png)
Aide :
Remplacer par la matrice antisymétrique :
![[\Omega] = \begin{pmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation48.png)
- Question 4
Aide :
Il s'exprime en fonction des différents éléments de la MCD et de sa dérivée.
pages_nanosats/exercice-equations-mouvement.html
Exercice
'Cinématique d'attitude avec les angles d'Euler'
pages_nanosats/exercice-equations-mouvement.html
Exercice
'Cinématique d'attitude avec les quaternions'
pages_nanosats/exercice-couples-perturbateurs.html
Exercice
'Couples perturbateurs agissant sur un CubeSat'
- Question 1
- Question 2
Aide :
C'est un CubeSat 3U et on sait qu'une unité représente un cube de 10 cm d'arête et de 1,3 kg.
- Question 3
Aide :
Comme première approximation, on peut considérer que le satellite est homogène et que son centre de masse se trouve parfaitement localisé en son centre. Les moments d'inertie principaux peuvent donc s'exprimer :
- Question 4
Aide :
Ils sont au nombre de 4.
- Question 5
Aide :
Pour la trainée atmosphérique :
- Déterminer l'aire projetée le long de la direction du mouvement.
- Exprimer la force de trainée atmosphérique :
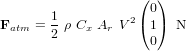
- Utiliser la position du centre de masse pour calculer les couples de trainée atmosphérique selon les trois axes principaux du satellite :
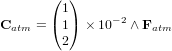
Aide :
Pour le gradient de gravité :
- L'axe +Y étant parallèle à la vitesse du satellite et la trajectoire étant circulaire, le rayon vecteur de la force de gravitation se décompose dans le plan X-Z
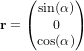 .
. - La matrice d'inertie s'exprime :
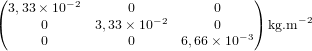
- Appliquer la formule vue dans le cours :
![\bold C_{GG} = \frac{3 \ \mu}{r^3} \bold r \wedge \left([I] \bold r \right)](../pages_nanosats/equations_nanosats-setester/equation94.png)
- En exprimant le produit vectoriel, on se rend compte que le maximum correspond à
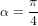 .
.
Aide :
Pour la pression solaire :
- Consider l'un des pires cas, c'est à dire que les faces +X ou +Y sont parfaitement orientées vers le Soleil, et en déduire la surface exposée et l'angle d'incidence.
- Exprimer la force de pression de radiation solaire :
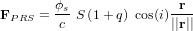 avec
avec 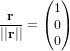 et
et 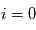 .
. - Utiliser la position du centre de masse pour exprimer les couples de pression de radiation solaire selon les trois axes principaux du satellite :
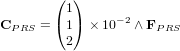
Aide :
Pour le gradient magnétique :
- Identifier le pire alignement entre le satellite et le champ magnétique terrestre : lorsque le dipôle résiduel et le champ magnétique sont perpendiculaires.
- Le couple correspondant est simplement le produit de ces deux valeurs :
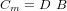
- Question 6
- Question 7
Aide :
Les magnéto-coupleurs doivent pouvoir compenser tous les couples perturbateurs agissant sur le satellite. Ils doivent donc au moins fournir  N.m.
N.m.
Aide :
Rappelons les équations permettant de calculer le couple magnétique et le moment dipolaire :
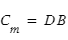 et
et 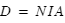 , où N est le nombre de spire de la bobine.
, où N est le nombre de spire de la bobine.
pages_nanosats/exercice-propulsion.html
Exercice
- Question 1
Aide :
Cette relation s'obtient facilement à partir de la relation exprimant la force en fonction de la vitesse d'expulsion et la définition de l'impulsion spécifique.
- Question 2
Aide :
Le CubeSat faisant 3 unités, on peut estimer que sa masse totale est de 4 kg.
- Question 3
Aide :
Il faut sommer la masse de carburant et la masse sèche afin d'obtenir la masse du système de propulsion dans son ensemble. Ceci n'est qu'une première approximation, notamment car on ne prend pas en compte la masse supplémentaire correspondant à des réservoirs plus gros.
- Question 4
- Question 5
Aide :
Dans ce cas, la durée de la manœuvre est directement liée à la force de poussée.
pages_nanosats/exercice-lois-de-commande.html
Exercice
'Étude d'un ressort'
- Question 1
- Question 2
- Question 3
Aide :
Il faut prendre la transformée de Laplace de l'équation exprimée précédemment.
Aide :
Les conditions initiale sont supposées nulles.
- Question 4
- Question 5
Aide :
C'est une simple multiplication.
 Prérequis
Prérequis Livres conseillés
Livres conseillés

































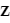 coïncide avec l'axe de rotation de la Terre et les axes
coïncide avec l'axe de rotation de la Terre et les axes 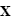 et
et 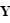 sont fixés par rapport à la Terre.
sont fixés par rapport à la Terre.
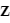 pointe vers le
pointe vers le 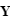 est normal au plan orbital.
est normal au plan orbital.
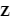 est ainsi aligné avec le
est ainsi aligné avec le 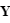 pointe le long de l'inverse du moment cinétique orbital. L'axe
pointe le long de l'inverse du moment cinétique orbital. L'axe 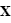 vient compléter le trièdre.
vient compléter le trièdre.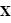 est parallèle au vecteur vitesse du satellite,
est parallèle au vecteur vitesse du satellite, 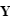 est le vecteur normal à la trajectoire à la position du satellite dans le plan de l'orbite et orienté vers le centre de la Terre, et
est le vecteur normal à la trajectoire à la position du satellite dans le plan de l'orbite et orienté vers le centre de la Terre, et 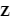 est parallèle et de même sens que le moment cinétique orbital.
est parallèle et de même sens que le moment cinétique orbital.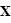 ,
, 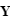 et
et 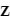 .
.
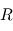 , avec les axes
, avec les axes 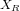 et
et 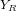 , incliné par rapport à un référentiel
, incliné par rapport à un référentiel 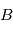 , d'axes
, d'axes 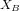 et
et 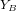 , d'un angle
, d'un angle  . Le vecteur
. Le vecteur  peut être exprimé dans ces deux systèmes sous forme matricielle :
peut être exprimé dans ces deux systèmes sous forme matricielle : et
et 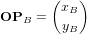 .
.
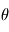 . Cette matrice transforme le vecteur
. Cette matrice transforme le vecteur  du premier référentiel
du premier référentiel  vers le second
vers le second 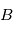 .
.
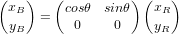
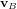 dans
dans 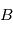 à partir de son expression
à partir de son expression 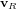 dans
dans 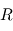 s'écrit :
s'écrit :
![\bold v_B = [T]_{B|R} \bold v_R](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation20.png) avec
avec ![[T]_{B|R} = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_x \cdot \bold R_y & \bold B_x \cdot \bold R_z \\ \bold B_y \cdot \bold R_x & \bold B_y \cdot \bold R_y & \bold B_y \cdot \bold R_z \\ \bold B_z \cdot \bold R_x & \bold B_z \cdot \bold R_y & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation21.png)
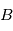 par rapport à
par rapport à 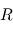 . On l'appelle également matrice de rotation ou matrice de transformation des coordonnées de
. On l'appelle également matrice de rotation ou matrice de transformation des coordonnées de 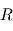 vers
vers 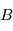 .
.
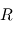 autour de chacun de ses trois axes se retrouvent décrites par les matrices de rotation suivantes :
autour de chacun de ses trois axes se retrouvent décrites par les matrices de rotation suivantes :
![[T(\theta_1)]_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_{\theta_1} & s_{\theta_1} \\ 0 & -s_{\theta_1} & c_{\theta_1} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation27.png) ,
, ![[T(\theta_2)]_2 = \begin{pmatrix} c_{\theta_2} & 0 & -s_{\theta_2} \\ 0 & 1 & 0 \\ s_{\theta_2} & 0 & c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation28.png) et
et ![[T(\theta_3)]_3 = \begin{pmatrix} c_{\theta_3} & s_{\theta_3} & 0 \\ -s_{\theta_3} & c_{\theta_3} & 0 \\ 0 & 0 & 1 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation29.png)
![[T(\theta_i)]_i](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation30.png) indique une rotation d'angle
indique une rotation d'angle 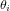 autour du i-ème axe du référentiel fixé sur le corps.
autour du i-ème axe du référentiel fixé sur le corps.
![[T]^{-1} = [T]^T](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation32.png) et
et ![[T][T]^T = [I] = [T]^T[T]](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation33.png)
![\bold v_R = [T]_{R|B}^T \bold v_B = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_y \cdot \bold R_x & \bold B_z \cdot \bold R_x \\ \bold B_x \cdot \bold R_y & \bold B_y \cdot \bold R_y & \bold B_z \cdot \bold R_y \\ \bold B_x \cdot \bold R_z & \bold B_y \cdot \bold R_z & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation34.png)
![[T]_{sat|inertiel} = [T]_{sat|orbite} [T]_{orbite|Terre} [T]_{Terre|inertiel}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation35.png)
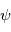 , autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).
, autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).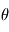 , autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).
, autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).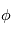 , ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
, ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).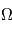 , autour de l'axe
, autour de l'axe  . La deuxième rotation est l'inclinaison,
. La deuxième rotation est l'inclinaison, 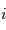 , autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie,
, autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie, 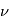 , autour de la normale à l'orbite.
, autour de la normale à l'orbite.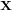 du satellite.
du satellite.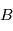 par rapport au référentiel
par rapport au référentiel 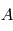 :
:
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation46.png)
![[T]_{B|A} = [T(\theta_1)]_1 [T(\theta_2)]_2 [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation47.png) , donc :
, donc : ![[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation48.png)
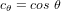 et
et 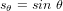 .
.

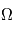 ), l'inclinaison (
), l'inclinaison (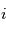 ) et l'anomalie vraie (
) et l'anomalie vraie (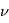 ).
).

 . C'est un vecteur unité possédant les mêmes composantes dans les référentiels de départ et d'arrivée :
. C'est un vecteur unité possédant les mêmes composantes dans les référentiels de départ et d'arrivée :  . Ainsi, 4 grandeurs sont requises pour décrire de façon non-ambigüe l'orientation par rapport à un référenciel : les 3 composantes de
. Ainsi, 4 grandeurs sont requises pour décrire de façon non-ambigüe l'orientation par rapport à un référenciel : les 3 composantes de  et l'angle de la rotation,
et l'angle de la rotation, 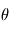 .
.
 . Le quaternion contient la même information qu'une MCD à 9 éléments, tout en s'affranchissant des problèmes de singularité rencontrés avec les angles d'Euler. Ils sont à la fois compacts et une représentation efficace de l'orientation pour la détermination d'attitude. Une même rotation est représentée par les quaternions
. Le quaternion contient la même information qu'une MCD à 9 éléments, tout en s'affranchissant des problèmes de singularité rencontrés avec les angles d'Euler. Ils sont à la fois compacts et une représentation efficace de l'orientation pour la détermination d'attitude. Une même rotation est représentée par les quaternions  et
et 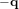 . On note également que les quatre paramètres d'Euler ne sont pas indépendants, mais contraints par la relation suivante :
. On note également que les quatre paramètres d'Euler ne sont pas indépendants, mais contraints par la relation suivante :
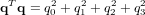
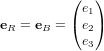 , les paramètres d'Euler sont :
, les paramètres d'Euler sont : 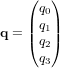 , avec
, avec 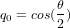 ,
, 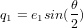 ,
, 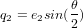 et
et 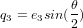 .
.
![[T]_{B|R} = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation15.png)
 peut opérer sur un vecteur vivant lui dans
peut opérer sur un vecteur vivant lui dans  . Notons tout d'abord qu'un vecteur est un quaternion pur dont la partie réelle est nulle. L'opérateur
. Notons tout d'abord qu'un vecteur est un quaternion pur dont la partie réelle est nulle. L'opérateur 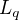 décrivant une rotation s'exprime avec le quaternion unitaire
décrivant une rotation s'exprime avec le quaternion unitaire  :
: 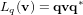 . Le vecteur ainsi obtenu conserve la longueur du vecteur initial, comme le fait une rotation. Cet opérateur se développe de la manière suivante :
. Le vecteur ainsi obtenu conserve la longueur du vecteur initial, comme le fait une rotation. Cet opérateur se développe de la manière suivante :
 et
et  décrivant respectivement les opérateurs
décrivant respectivement les opérateurs 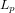 et
et 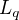 . Le premier opérateur est appliqué au vecteur
. Le premier opérateur est appliqué au vecteur  pour obtenir le vecteur
pour obtenir le vecteur 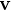 , puis le second est appliqué à
, puis le second est appliqué à 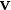 pour obtenir
pour obtenir  . La composition des opérateurs
. La composition des opérateurs 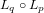 s'écrit :
s'écrit :
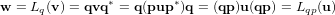
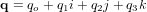
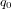 ,
, 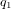 ,
, 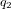 ,
, 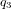 sont des nombres réels, et
sont des nombres réels, et 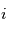 ,
, 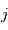 ,
, 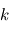 sont des symboles respectant les relations quaternioniques :
sont des symboles respectant les relations quaternioniques :
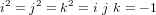
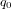 est appelé partie réelle de
est appelé partie réelle de  et
et 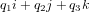 est appelé partie imaginaire.
est appelé partie imaginaire.
 où s'applique l'addition composant par composant. Soient deux quaternions
où s'applique l'addition composant par composant. Soient deux quaternions  et
et  :
:
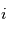 ,
, 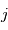 et
et 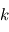 sont définis de la manière suivante :
sont définis de la manière suivante :
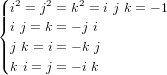
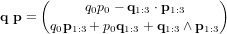
![\bold q \ \bold p = [Q(\bold q)] \bold p](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation53.png)
![[Q(\bold q)] = \begin{pmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation54.png) .
.
 et
et  sont :
sont :
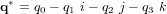 et
et 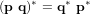
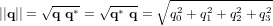 et
et 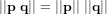
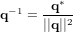
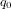 est la partie scalaire de
est la partie scalaire de 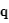 et
et 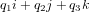 est la partie vectorielle. Ainsi, la partie scalaire est toujours réelle et la partie vectorielle toujours purement imaginaire. Bien que l'on ait dit qu'un quaternion est un vecteur dans un espace à 4 dimensions, il est courant de définir un vecteur pour la partie imaginaire d'un quaternion :
est la partie vectorielle. Ainsi, la partie scalaire est toujours réelle et la partie vectorielle toujours purement imaginaire. Bien que l'on ait dit qu'un quaternion est un vecteur dans un espace à 4 dimensions, il est courant de définir un vecteur pour la partie imaginaire d'un quaternion : 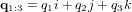 et
et 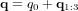
 représente sa position,
représente sa position, 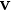 sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit
sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit  . L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen
. L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen 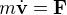 ou
ou  , avec
, avec 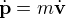 la quantité de mouvement,
la quantité de mouvement, 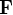 la résultante des forces appliquées et
la résultante des forces appliquées et 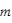 la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire
la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire 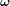 . Les forces et quantités de mouvement sont quant à elles remplacées par le couple
. Les forces et quantités de mouvement sont quant à elles remplacées par le couple  et le moment angulaire
et le moment angulaire  . La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
. La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
 allant de l'origine du repère au centre de l'objet
allant de l'origine du repère au centre de l'objet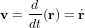
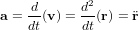
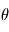 par rapport à sa position originelle
par rapport à sa position originelle est un vecteur unitaire dans la direction de l'axe de rotation, la vitesse angulaire est alors obtenue par :
est un vecteur unitaire dans la direction de l'axe de rotation, la vitesse angulaire est alors obtenue par : 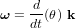
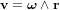
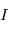 à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté
à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté 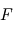 , on peut écrire :
, on peut écrire :
![\bold{r}_I = [T]_{I|F} \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation10.png)
![\bold{v}_I = \frac{d}{dt} (\bold{r}_I) = [T]_{I|F} \ \frac{d}{dt} (\bold{r}_F) + \frac{d}{dt}([T]_{I|F}) \ \bold{r}_F = [T]_{I|F} \ \frac{d}{dt}(\bold{r}_F) + ([T]_{I|F} \ [\Omega]) \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation11.png)
![\bold{v}_I = [T]_{I/F} ([\Omega] \ \bold{r}_F + \bold{v}_F)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation12.png)
![\bold{a}_I = \frac{d}{dt}(\bold{v}_I) = \frac{d}{dt}([T]_{I/F}) ([\Omega] \ \bold{r}_F + \bold{v}_F) + [T]_{I/F} \left[ \frac{d}{dt}([\Omega]) \ \bold{r}_F + [\Omega] \ \frac{d}{dt}(\bold{r}_F) + \frac{d}{dt}(\bold{v}_F)\right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation13.png)
![\bold{a}_I = [T]_{I/F} \left[ [\Omega] \left([\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega] \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation14.png)
![\bold{F}_F = [T]_{F/I} \left( m \ \bold{a}_I \right) = m \left[ [\Omega] \left( [\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega]) \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation15.png)
![\frac{d}{dt} \left( [\Omega] \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation16.png) est l'accélération angulaire. On introduit ici les accélérations centripète
est l'accélération angulaire. On introduit ici les accélérations centripète ![[\Omega] \left( [\Omega] \ \bold{r}_F \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation17.png) et de Coriolis
et de Coriolis ![2 \ [\Omega] \ \bold{v}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation18.png) .
.
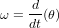 .
.
 en rotation par rapport à un référentiel
en rotation par rapport à un référentiel  avec une vitesse angulaire
avec une vitesse angulaire 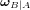 . Si la matrice d'attitude s'exprime
. Si la matrice d'attitude s'exprime ![[T]_{B|A}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation23.png) , alors :
, alors :
![\frac{d}{dt} \left( [T]_{B|A} \right) = -[\Omega] \ [T]_{B|A}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation24.png) avec
avec ![[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation25.png)
 représentant la vitesse angulaire du référentiel
représentant la vitesse angulaire du référentiel  par rapport au référentiel
par rapport au référentiel  , avec
, avec 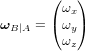 .
.
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation30.png) conduisant du référentiel
conduisant du référentiel  au référentiel
au référentiel  l'équation de la cinématique est réécrite :
l'équation de la cinématique est réécrite :
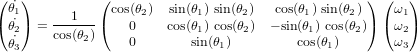
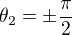 ).
).
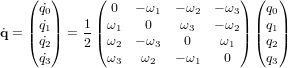
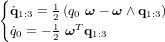
 de la force
de la force  par rapport à au point
par rapport à au point  est défini par :
est défini par :
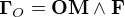
 est non nul. Dans ce cas, il est possible de montrer que le moment global d'un tel couple par rapport à n'importe quel point est égal au produit vectoriel caractéristique du couple :
est non nul. Dans ce cas, il est possible de montrer que le moment global d'un tel couple par rapport à n'importe quel point est égal au produit vectoriel caractéristique du couple :
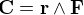
 est le vecteur allant du centre de gravité du système au point d'application de la force
est le vecteur allant du centre de gravité du système au point d'application de la force 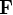 . Si, pour un corps solide sans contraine, une force va accélérer son centre de masse, un couple aura lui pour effet d'induire un mouvement de rotation autour du centre de masse.
. Si, pour un corps solide sans contraine, une force va accélérer son centre de masse, un couple aura lui pour effet d'induire un mouvement de rotation autour du centre de masse.
![[I] = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{n}{m_i \left(y_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & -\sum_{i=1}^{n}{m_i \ x_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ z_i} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+y_i^2 \right)} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation9.png) ,
,
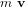 . Considérons un système matériel qui est la somme de
. Considérons un système matériel qui est la somme de 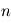 masses ponctuelles. Le moment angulaire, ou moment cinétique, par rapport à un point
masses ponctuelles. Le moment angulaire, ou moment cinétique, par rapport à un point  est le moment de la quantité de mouvement
est le moment de la quantité de mouvement  par rapport à ce point
par rapport à ce point  :
:
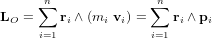
![[I]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation16.png) et de la vitesse angulaire
et de la vitesse angulaire  :
:
![\bold L = [I] \ \boldsymbol\omega](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation18.png)
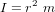 est le moment d'inertie d'une masse ponctuelle,
est le moment d'inertie d'une masse ponctuelle,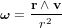 est le moment angulaire de la particule par rapport à l'origine.
est le moment angulaire de la particule par rapport à l'origine. dont l'origine se trouve au centre de masse du satellite. Notons
dont l'origine se trouve au centre de masse du satellite. Notons 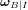 le vecteur vitesse angulaire du référentiel
le vecteur vitesse angulaire du référentiel 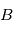 par rapport au référentiel inertiel
par rapport au référentiel inertiel 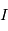 .
.
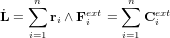
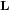 est le moment angulaire du corps solide par rapport à son centre de masse et
est le moment angulaire du corps solide par rapport à son centre de masse et 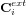 sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
![\bold L = [I] \boldsymbol\omega+ \bold h](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation28.png) :
:
![[I] \dot{\boldsymbol\omega} = \sum_{i=1}^{n}{\bold C_i^{ext} - \dot{\bold h} - \dot{[I]} \boldsymbol\omega}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation29.png)




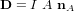
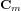 est donné par :
est donné par :
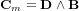
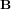 (en T) représente le champ magnétique.
(en T) représente le champ magnétique.
 , où
, où  (en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique,
(en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique,  la distance entre le satellite et le centre du corps , et enfin
la distance entre le satellite et le centre du corps , et enfin 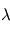 une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.


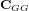 de la manière suivante :
de la manière suivante :
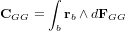
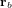 est le vecteur position allant du centre de gravité du satellite à l'élément de masse et
est le vecteur position allant du centre de gravité du satellite à l'élément de masse et 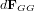 est la force de gravité s'appliquant sur ce même élément de masse :
est la force de gravité s'appliquant sur ce même élément de masse :
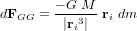
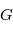 est la constante gravitationnelle, elle vaut
est la constante gravitationnelle, elle vaut 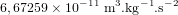 ,
, 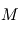 est la masse du corps attracteur et
est la masse du corps attracteur et 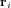 est le vecteur position de l'élément de masse
est le vecteur position de l'élément de masse 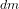 dans le référentiel inertiel (
dans le référentiel inertiel (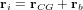 ). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
![\bold C_{GG} = \frac{3 \ G \ M}{|\bold r_{CG}|^5} \ \bold r_{CG} \wedge \left([I] \ \bold r_{CG} \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation20.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation21.png) du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.


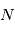 surfaces d'aire
surfaces d'aire 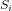 , dont la normale orientée vers l'extérieur est notée
, dont la normale orientée vers l'extérieur est notée 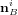 dans le référentiel du satellite et de coefficient de réflexion
dans le référentiel du satellite et de coefficient de réflexion 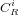 (on lui attribue généralement une valeur de 0,6 pour un petit satellite).
(on lui attribue généralement une valeur de 0,6 pour un petit satellite).
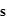 . L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
. L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
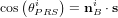
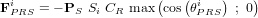 avec
avec 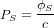
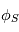 (en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et
(en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et 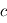 (en m/s) est la vitesse de la lumière.
(en m/s) est la vitesse de la lumière.
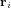 le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
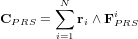
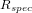 ;
;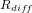 ;
;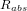 .
.![\bold F_{PRS}^i = -P_S \ S_i \left[ 2 \left( \frac{R_{diff}^i}{3} + R_{spec}^i \ \textup{cos} \left(\theta_{PRS}^i \right) \right) \bold n_B^i + \left( 1-R_{spec}^i \right) \bold s \right] \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation37.png)
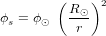
 le flux émis à la surface du Soleil et
le flux émis à la surface du Soleil et  le rayon du Soleil.
le rayon du Soleil.  est estimé en appliquant la loi de Stefan-Boltzmann au Soleil considéré comme un corps noir :
est estimé en appliquant la loi de Stefan-Boltzmann au Soleil considéré comme un corps noir :
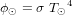
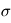 la constante de Stefan-Boltzmann et
la constante de Stefan-Boltzmann et 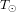 la température thermodynamique du corps noir. À la distance moyenne Terre-Soleil (1 UA) l'irradiance solaire (ou constante solaire) vaut 1362 W.m-2.
la température thermodynamique du corps noir. À la distance moyenne Terre-Soleil (1 UA) l'irradiance solaire (ou constante solaire) vaut 1362 W.m-2.
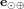 (Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
(Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
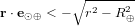


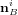 , pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
, pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
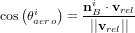
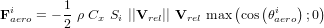
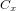 est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
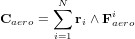
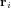 est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.

 si
si  et
et 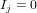 si
si 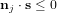 , avec
, avec  le vecteur unité pointant vers la normale extérieure à la photocellule
le vecteur unité pointant vers la normale extérieure à la photocellule  et
et  le vecteur unité allant du satellite au Soleil. Le champ de vue est un cône d'ouverture limitée.
le vecteur unité allant du satellite au Soleil. Le champ de vue est un cône d'ouverture limitée.
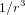 de son champ magnétique (
de son champ magnétique (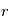 étant l'altitude du satellite). On les utilise de différentes manières, l'une d'entre elles étant de calculer le champ magnétique instantané afin de mieux calibrer les couples à générer par les
étant l'altitude du satellite). On les utilise de différentes manières, l'une d'entre elles étant de calculer le champ magnétique instantané afin de mieux calibrer les couples à générer par les 



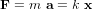 , avec
, avec  l'accélération,
l'accélération, 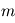 la masse,
la masse, 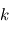 la constante de raideur du ressort et
la constante de raideur du ressort et  le déplacement du ressort.
le déplacement du ressort.


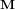 (en A.m2). En présence d'un champ magnétique tel que le champ magnétique terrestre
(en A.m2). En présence d'un champ magnétique tel que le champ magnétique terrestre 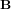 , le magnéto-coupleur fournit alors un couple
, le magnéto-coupleur fournit alors un couple 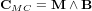 . On distingue trois types de magnéto-coupleurs :
. On distingue trois types de magnéto-coupleurs :
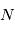 , de l'aire de la section de la bobine
, de l'aire de la section de la bobine 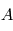 et du courant d'intensité
et du courant d'intensité 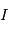 la parcourant. Ce moment dipolaire s'exprime alors
la parcourant. Ce moment dipolaire s'exprime alors 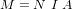 et est orienté perpendiculairement au plan de la bobine. Il est ainsi nécessaire d'effectuer de nombreux tours ou d'augmenter la section de la bobine si l'on veut obtenir un moment dipolaire plus important à intensité égale.
et est orienté perpendiculairement au plan de la bobine. Il est ainsi nécessaire d'effectuer de nombreux tours ou d'augmenter la section de la bobine si l'on veut obtenir un moment dipolaire plus important à intensité égale.


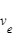 qui représente la vitesse relative entre le satellite et le carburant expulsé) avec une quantité de mouvement associée
qui représente la vitesse relative entre le satellite et le carburant expulsé) avec une quantité de mouvement associée 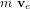 , ce qui, par conservation de la quantité de mouvement, résulte en une
, ce qui, par conservation de la quantité de mouvement, résulte en une ![\bold F = \dot m \bold v_e \ \textup{[N]}](../pages_nanosats/equations_nanosates-comprendre-materiel-propulsion/equation3.png) .
.
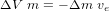
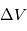 ) du satellite :
) du satellite : 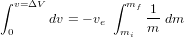
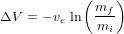
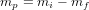 , il ne reste plus qu'à déplacer les termes de l'équation précédente afin d'obtenir :
, il ne reste plus qu'à déplacer les termes de l'équation précédente afin d'obtenir : 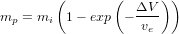
![I_{tot} = \int_{0}^{\tau}{F \ dt} = v_e \ \int_{0}^{m_p}{dm} = v_e \ m_p \ \textup{[N.s]}](../pages_nanosats/equations_nanosates-comprendre-materiel-propulsion/equation10.png) .
.
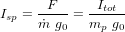 , avec
, avec  le champ standard de la pesanteur (9,81 m.s-2). Les impulsions spécifiques sont notées en secondes et parfois données en N.s.kg-1, ce qui correspond à la formule précédente multipliée par l'accélération standard de la pesanteur, donnant l'impulsion délivrée par unité de masse.
le champ standard de la pesanteur (9,81 m.s-2). Les impulsions spécifiques sont notées en secondes et parfois données en N.s.kg-1, ce qui correspond à la formule précédente multipliée par l'accélération standard de la pesanteur, donnant l'impulsion délivrée par unité de masse.
![I_{ssp} = \frac{I_{tot}}{m_{ps} \ g_0} \ \textup{[s]}](../pages_nanosats/equations_nanosates-comprendre-materiel-propulsion/equation13.png) .
.




 , où
, où  et
et 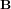 sont respectivement le flux de courant ionique dans le plasma et le champ magnétique. Il en résulte une force de poussée sur le satellite dans la direction opposée.
sont respectivement le flux de courant ionique dans le plasma et le champ magnétique. Il en résulte une force de poussée sur le satellite dans la direction opposée.
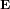 créant une force de Coulomb (
créant une force de Coulomb (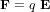 ). Les systèmes de propulsion électrostatiques nécessitent généralement l'installation d'un neutraliseur (cathode) qui fournit des électrons au faisceau d'ions, afin de conserver la neutralité électrique du jet.
). Les systèmes de propulsion électrostatiques nécessitent généralement l'installation d'un neutraliseur (cathode) qui fournit des électrons au faisceau d'ions, afin de conserver la neutralité électrique du jet.

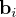 définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire
définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire 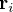 qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale
qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale  satisfaisant pour chaque observation i :
satisfaisant pour chaque observation i :
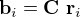
 permettant de transformer les vecteurs de référence
permettant de transformer les vecteurs de référence 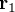 et
et 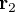 en vecteurs d'observation
en vecteurs d'observation 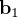 et
et 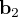 . Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD)
. Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD)  satisfaisant :
satisfaisant :
![\bold y_i = [C] \ \bold x_i](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation11.png) ,
,  ,
, 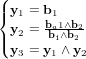
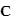 minimisant la fonction de moindres carrés :
minimisant la fonction de moindres carrés :
![L = \frac{1}{2} \ \sum_{i=1}^{n}{a_i \left| \bold b_i - [C] \bold r_i \right|^2}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation15.png)
![\bold x_k = [A]_k \ \bold x_{k-1} + [B]_k \ \bold u_{k-1} + \bold w_{k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation16.png)
![\bold z_k = [H]_k \ \bold x_k + \bold v_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation17.png)
 et
et  représentent respectivement les bruits de processus et de mesure. On les suppose indépendants, blancs et de distribution de probabilité normale.
représentent respectivement les bruits de processus et de mesure. On les suppose indépendants, blancs et de distribution de probabilité normale. ![[A]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation20.png) est la matrice qui relie l'état précédent k-1 à l'état actuel k,
est la matrice qui relie l'état précédent k-1 à l'état actuel k, ![[B]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation21.png) est la matrice qui relie l'entrée de commande
est la matrice qui relie l'entrée de commande  à l'état
à l'état  .
. ![[H]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation24.png) est la matrice reliant l'état
est la matrice reliant l'état  à sa mesure
à sa mesure  .
.
![\hat{\bold x}_{k|k-1} = [A]_k \ \hat{\bold x}_{k-1|k-1} + [B]_k \ \bold u_{k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation27.png)
![[P]_{k|k-1} = [A]_k \ [P]_{k-1|k-1} \ {[A]_k}^T + [Q]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation28.png)
![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation29.png) est la matrice de covariance du bruit de processus
est la matrice de covariance du bruit de processus  ,
, ![[P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation31.png) est la matrice d'estimation a priori de la covariance de l'erreur.
est la matrice d'estimation a priori de la covariance de l'erreur.
![[K]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation32.png) , puis générer une estimation de l'état a posteriori en incorporant la mesure. Enfin, on obtient la matrice de covariance de l'erreur d'estimation a posteriori
, puis générer une estimation de l'état a posteriori en incorporant la mesure. Enfin, on obtient la matrice de covariance de l'erreur d'estimation a posteriori ![[P]_{k|k}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation33.png) .
.
![[K]_k = [P]_{k|k-1} {[H]_k}^T \ {[S]_k}^{-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation34.png)
![\hat{\bold x}_{k|k} = \hat{\bold x}_{k|k-1} + [K]_k \ \bold y_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation35.png)
![[P]_k = \left( [I] - [K]_k \ [H]_k \right) [P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation36.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation37.png) est la matrice identité. Deux équations supplémentaires permettent d'obtenir l'innovation, ou résiduel,
est la matrice identité. Deux équations supplémentaires permettent d'obtenir l'innovation, ou résiduel,  , et la covariance de l'innovation
, et la covariance de l'innovation ![[S]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation39.png) :
:
![\bold y_k = \bold z_k - [H]_k \ \hat{\bold x}_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation40.png)
![[S]_k = [H]_k \ [P]_{k|k-1} \ {[H]_k}^T + [R]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation41.png)
![[R]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation42.png) du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus
du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus ![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation43.png) car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
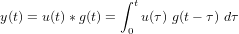
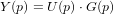
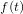 une fonction du temps. Sa transformée de Laplace unilatérale
une fonction du temps. Sa transformée de Laplace unilatérale 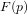 est
définie par
est
définie par 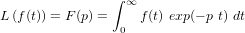 où
où 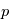 est la variable complexe.
est la variable complexe.
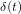 (Dirac)
(Dirac)
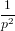
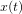
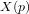
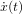
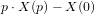
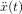
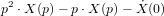
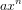
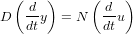 où
où 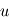 et
et 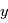 sont respectivement l'entrée et la sortie et
sont respectivement l'entrée et la sortie et 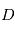 et
et 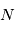 sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
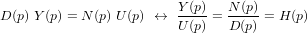
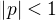 ).
).
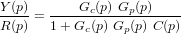



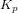
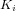
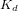
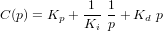
![[I] \ \ddot \theta (t) = u(t) + w(t)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation30.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation31.png) est la matrice d'inertie,
est la matrice d'inertie, 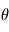 est l'angle,
est l'angle, 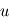 est le couple de contrôle et
est le couple de contrôle et 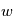 est le couple perturbateur extérieur.
est le couple perturbateur extérieur.
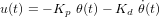
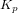 et
et 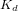 sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
![[I] \ \ddot \theta (t) + [K_d] \ \dot \theta (t) + [K_p] \ \theta(t) = w(t) \ \leftrightarrow \ I \ p^2 + [K_d] \ p + [K_p] = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation38.png)
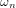 et
et 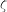 , respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
, respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
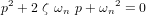
![[K_p] = [I] \ {\omega_n}^2](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation42.png) et
et ![[K_d] = 2 \ [I] \ \zeta \ \omega_n](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation43.png) . On choisit généralement le
. On choisit généralement le 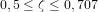 . Il est important de noter que l'information sur la dérivée provient de
. Il est important de noter que l'information sur la dérivée provient de  . Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
. Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
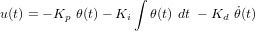
![[I] \ p^3 + [K_d] \ p^2 + [K_p] \ p + [K_i] = 0 \ \leftrightarrow \ \left( p^2 + 2 \ \zeta \ \omega_n \ p + {\omega_n}^2 \right) \left( p + \frac{1}{T} \right) = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation47.png)
 et
et  sont toujours la fréquence propre et le facteur d'amortissement, et
sont toujours la fréquence propre et le facteur d'amortissement, et  est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment :
est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment : ![[K_p] = [I] \left( {\omega_n}^2 + \frac{2 \ \zeta \ \omega_n}{T} \right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation51.png) ,
, ![[K_i] = [I] \ \frac{{\omega_n}^2}{T}](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation52.png) et
et ![[K_d] = [I] \left( 2 \ \zeta \ \omega_n + \frac{1}{T}\right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation53.png) . On choisit souvent la constante
. On choisit souvent la constante  telle que :
telle que : 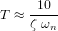 .
.

![[T] \ [T]^T = [I] = [T]^T \ [T]](../pages_nanosats/equations_nanosats-setester/equation1.png) .
.
![[T]_{B|A}](../pages_nanosats/equations_nanosats-setester/equation2.png) entre deux référentiels orthogonaux décrits par les vecteurs unitaires
entre deux référentiels orthogonaux décrits par les vecteurs unitaires 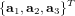 et
et 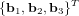 :
:
![\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = [T]_{B|A} \ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation5.png)
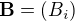 .
.
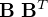 et conclure.
et conclure.
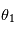 ,
, 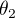 et
et 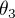 les trois angles d'Euler.
les trois angles d'Euler.
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation15.png) afin de passer du référentiel
afin de passer du référentiel 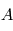 au référentiel
au référentiel 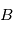 , on obtient bien la formule présentée dans le
, on obtient bien la formule présentée dans le ![[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation18.png)
![\begin{cases} \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} = [T(\theta_3)]_3 \ \begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} \\ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} = [T(\theta_2)]_2 \ \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} \\ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} = [T(\theta_1)]_1 \ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} \end{cases}](../pages_nanosats/equations_nanosats-setester/equation19.png)
![[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2](../pages_nanosats/equations_nanosats-setester/equation20.png) . Exprimer la MCD associée à cette séquence.
. Exprimer la MCD associée à cette séquence.
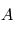 au référentiel
au référentiel 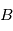 :
:
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation24.png)
![[T(\theta_1)]_1 = \begin{pmatrix} sin(\theta_1 / 2) \\ 0 \\ 0 \\ cos(\theta_1 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation25.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ sin(\theta_2 / 2) \\ 0 \\ cos(\theta_2 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation26.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ 0 \\ sin(\theta_3 / 2) \\ cos(\theta_3 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation27.png)
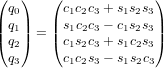
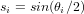 et
et 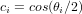
![\frac{d}{dt}([T]) = -[\Omega] \ [T]](../pages_nanosats/equations_nanosats-setester/equation32.png) avec
avec ![[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation33.png) et
et ![[T] = \begin{pmatrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation34.png)
![[T]](../pages_nanosats/equations_nanosats-setester/equation35.png) entre deux référentiels orthogonaux décrits par les vecteurs unitaires
entre deux référentiels orthogonaux décrits par les vecteurs unitaires 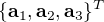 et
et 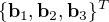 .
.
![[T]](../pages_nanosats/equations_nanosats-setester/equation38.png) .
.
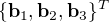 au vecteur
au vecteur 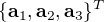 .
.
![\begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} = [T]^T \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation42.png)
 par rapport à
par rapport à 
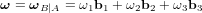 et l'insérer dans l'équation précédente.
et l'insérer dans l'équation précédente.
![\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \dot {[T]}^T \ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} + [T]^T \ \begin{pmatrix} \boldsymbol\omega \wedge \bold b_1 \\ \boldsymbol\omega \wedge \bold b_2 \\ \boldsymbol\omega \wedge \bold b_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation47.png)
![[\Omega] = \begin{pmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation48.png)
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation52.png) .
.
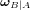 en fonction des vecteurs de vitesse angulaire précédents.
en fonction des vecteurs de vitesse angulaire précédents.
 et
et  en fonction de ceux de (B).
en fonction de ceux de (B).
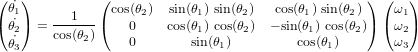
![[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2](../pages_nanosats/equations_nanosats-setester/equation62.png) . Exprimer alors l'équation de la cinématique.
. Exprimer alors l'équation de la cinématique.
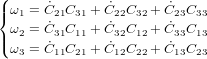
![[T] = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation65.png)
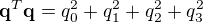
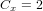
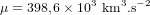
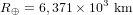
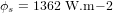
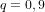
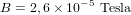
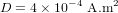
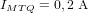
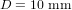

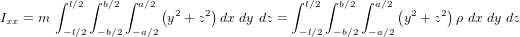
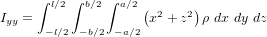
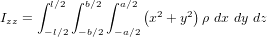
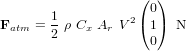
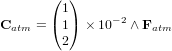
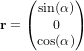 .
.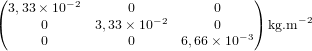
![\bold C_{GG} = \frac{3 \ \mu}{r^3} \bold r \wedge \left([I] \bold r \right)](../pages_nanosats/equations_nanosats-setester/equation94.png)
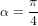 .
.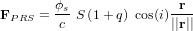 avec
avec 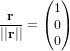 et
et  .
.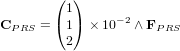
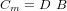
 N.m.
N.m.
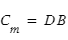 et
et 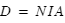 , où N est le nombre de spire de la bobine.
, où N est le nombre de spire de la bobine.

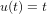 . Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :
. Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :