Présentation mathématique

Auteur: Gary Quinsac

William Rowan Hamilton

Peinture de Sir William Rowan Hamilton.

Crédit : Domaine public

Les quaternions sont un système de nombres premièrement décrits par William Rowan Hamilton en 1843 appliqué à la mécanique et à l'espace à 3 dimensions.

William Rowan Hamilton

Sir William Rowan Hamilton (04/08/1805 - 02/09/1865) est un mathématicien, physicien et astronome irlandais (né et mort à Dublin). Outre sa découverte des quaternions, il contribua également au développement de l'optique, de la dynamique et de l'algèbre. Ses recherches se révélèrent importantes pour le développement de la mécanique quantique.

Définition mathématique

Un quaternion q est une expression de la forme :

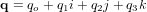
$\bold q = q_o + q_1 i + q_2 j + q_3 k$

où 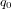, , 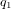, 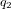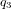sont des nombres réels, et 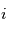, , 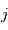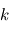sont des symboles respectant les relations quaternioniques :

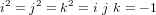
$i^2 = j^2 = k^2 = i \ j \ k = -1$

Par analogie avec les nombres complexes, 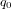est appelé partie réelle de $\bold q$ et 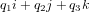est appelé partie imaginaire.
L'ensemble des quaternions est un espace vectoriel de dimension 4 et de base 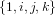$\{1,i,j,k\}$ où s'applique l'addition composant par composant. Soient deux quaternions $\bold p$ et $\bold q$ :

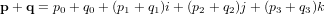
$\bold p + \bold q = p_0 + q_0 + (p_1 + q_1)i + (p_2 + q_2)j + (p_3 + q_3)k$
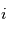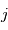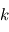Afin d'introduire la multiplication, il faut d'abord introduire le produit hamiltonien. Les produits des éléments de base , et sont définis de la manière suivante :

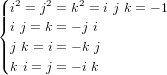
$\begin{cases} i^2 = j^2 = k^2 = i \ j \ k = -1 \\ i \ j = k = -j \ i \\ j \ k = i = -k \ j \\ k \ i = j = -i \ k \end{cases}$

La multiplication de quaternions est associative et distributive, mais pas commutative en général. Pour les quaternions q et p elle est définie par :

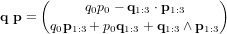
$\bold q \ \bold p = \binom{q_0 p_0 - \bold q_{1:3} \cdot \bold p_{1:3}}{q_0 \bold p_{1:3} + p_0 \bold q_{1:3} + \bold q_{1:3} \wedge \bold p_{1:3}}$

Elle peut être représentée par une multiplication matricielle. Dans ce cas, une matrice composée de valeurs du premier quaternion vient multiplier le second quaternion, tel que : $\bold q \ \bold p = [Q(\bold q)] \bold p$

avec $[Q(\bold q)] = \begin{pmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{pmatrix}$ .
Le conjugué, la norme et l'inverse des quaternions $\bold p$ et $\bold q$ sont :

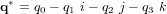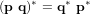
$\bold q^* = q_0 - q_1 \ i - q_2 \ j - q_3 \ k$ et $(\bold p \ \bold q)^* = \bold q^* \ \bold p^*$

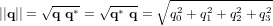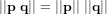
$||\bold q|| = \sqrt{\bold q \ \bold q^*} = \sqrt{\bold q^* \ \bold q} = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}$ et $||\bold p \ \bold q|| = ||\bold p|| \ ||\bold q||$

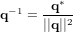
$\bold q^{-1} = {{\bold q^*} \over {||\bold q||^2}}$

Autre représentation

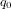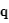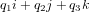Une autre façon de présenter un quaternion consiste à dire que q_0 est la partie scalaire de vecteur(q) et q_1 i + q_2 j + q_3 k est la partie vectorielle. Ainsi, la partie scalaire est toujours réelle et la partie vectorielle toujours purement imaginaire. Bien que l'on ait dit qu'un quaternion est un vecteur dans un espace à 4 dimensions, il est courant de définir un vecteur pour la partie imaginaire d'un quaternion : 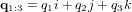$\bold q_{1:3} = q_1 i + q_2 j + q_3 k$ et $\bold q = q_0+\bold q_{1:3}$