Gradient de gravité

Auteur: Gary Quinsac

Gradient de gravité

Géométrie du couple de gradient de gravité.

Crédit : Gary Quinsac

Le gradient de gravité résulte de l'interaction du champ gravitationnel, lui-même proportionnel à l'inverse du carré de la distance, avec un satellite de masse non ponctuelle. L'accélération gravitationnelle est la plus forte sur la partie du satellite la plus proche du corps attracteur. Le gradient est à l'origine d'un couple qui peut être utilisé pour contrôler passivement l'attitude du satellite. Les couples de gradient de gravité apparaissent lorsque le centre de gravité d'un satellite en orbite n'est pas aligné avec le centre de masse par rapport à la verticale locale.

Centres de masse et de gravité

Le centre de masse, également appelé centre d'inertie, est le barycentre des masses d'un objet. Le centre de gravité, quant à lui, est le point d'application de la résultante des forces de gravité. Si ceux-ci sont souvent confondus, ce n'est plus le cas lorsque le champ de gravitation n'est plus uniforme dans le corps en question.

On exprime le gradient de gravité 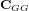$\bold C_{GG}$ de la manière suivante :

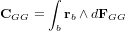
$\bold C_{GG} = \int_{b}{\bold r_b \wedge d \bold F_{GG}}$

où 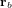$\bold r_b$ est le vecteur position allant du centre de gravité du satellite à l'élément de masse et 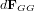$d \bold F_{GG}$ est la force de gravité s'appliquant sur ce même élément de masse :

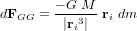
$d \bold F_{GG} = \frac{-G \ M}{|{\bold r_i}^3|} \ \bold r_i \ dm$

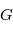est la constante gravitationnelle, elle vaut 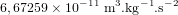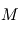$6,67259 \times 10^{-11} \ \textup{m}^{3}.\textup{kg}^{-1}.\textup{s}^{-2}$ , est la masse du corps attracteur et 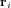$\bold r_i$ est le vecteur position de l'élément de masse 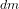dans le référentiel inertiel ( 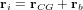$\bold r_i = \bold r_{CG} + \bold r_b$ ). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :

$\bold C_{GG} = \frac{3 \ G \ M}{|\bold r_{CG}|^5} \ \bold r_{CG} \wedge \left([I] \ \bold r_{CG} \right)$

Ce couple dépend de la matrice d'inertie [I] du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.

Stabilisation par gradient de gravité

Cette technique de contrôle d'attitude passive est assez utilisée pour des satellites en orbite terrestre devant pointer au nadir. Elle consiste à faire intéragir un satellite de forme particulière avec le champ gravitationnel afin de contraindre son orientation. Une masse peut être montée au bout d'un mât perpandiculaire à l'orbite afin de créer un moment d'inertie minimum selon cet axe. Cette masse étant plus proche, elle est plus attirée. Le satellite aura alors tendance à aligner cet axe d'inertie vers la verticale à l'orbite (qui est la direction d'attraction gravitationnelle).

Aller plus loin

Cours sur la gravitation