Cinématique d'attitude

Auteur: Gary Quinsac

La simulation et l'estimation d'attitude nécessitent généralement des représentations simples de l'attitude, telles que celles présentées dans le chapitre du même nom. Les équations différentielles de la cinématique peuvent ainsi être obtenues pour ces différentes représentations. Les démonstrations de ces équations sont proposées en exercices.

La cinématique d'attitude relie des vitesses angulaires à des orientations dans l'espace. Si cela peut sembler simple dans le cas d'une rotation autour d'un axe fixe, cela devient beaucoup moins intuitif dans le cas d'un mouvement plus général, où l'axe de rotation varie au cours du temps. Pour un corps en rotation autour d'un axe fixe, l'orientation par rapport à cet axe peut être déterminée en intégrant la vitesse angulaire ω, puisque 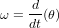$\omega = \frac{d}{dt}(\theta)$ .

MCD

Dans le cas général, la matrice exprimant le taux de variation de l'attitude est plus complexe. Considérons un référentiel 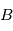en rotation par rapport à un référentiel 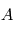avec une vitesse angulaire 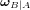$\boldsymbol\omega_{B|A}$ . Si la matrice d'attitude s'exprime $[T]_{B|A}$ , alors :

$\frac{d}{dt} \left( [T]_{B|A} \right) = -[\Omega] \ [T]_{B|A}$ avec $[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}$

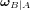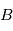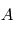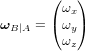La matrice d'attitude se retrouve multipliée par une matrice anti-symétrique qui est définie à partir du vecteur $\boldsymbol\omega_{B|A}$ représentant la vitesse angulaire du référentiel par rapport au référentiel , avec $\boldsymbol\omega_{B|A} = \begin{pmatrix} \omega_x \\ \omega_y \\ \omega_z \end{pmatrix}$ .

Dans ce cas, nous avons utilisé une MCD.

Angles d'Euler

Il est également possible d'exprimer cette équation différentielle en utilisant les angles d'Euler. En reprenant la séquence de rotations $[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$ conduisant du référentiel 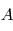au référentiel 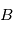l'équation de la cinématique est réécrite :

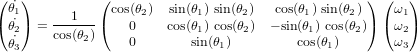
$\begin{pmatrix} \dot{\theta_1} \\ \dot{\theta_2} \\ \dot{\theta_3} \end{pmatrix} = \frac{1}{\textup{cos}(\theta_2)} \begin{pmatrix} \textup{cos}(\theta_2) & \textup{sin}(\theta_1) \ \textup{sin}(\theta_2) & \textup{cos}(\theta_1) \ \textup{sin}(\theta_2) \\ 0 & \textup{cos}(\theta_1) \ \textup{cos}(\theta_2) & -\textup{sin}(\theta_1) \ \textup{cos}(\theta_2) \\ 0 & \textup{sin}(\theta_1) & \textup{cos}(\theta_1) \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}$

En connaissant la vitesse angulaire d'un référentiel par rapport à l'autre en fonction du temps il est possible de déterminer la position au cours du temps d'un référentiel par rapport à l'autre. Néanmoins, l'intégration nécessite le calcul de fonctions trigonométriques ainsi que des singularités (ici 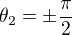$\theta_2 = \pm \frac{\pi}{2}$ ).

Quaternions

Dans le cas des quaternions, l'expression de l'équation de la cinématique se retrouve simplifiée :

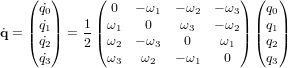
$\dot{\bold q} = \begin{pmatrix} \dot{q_0} \\ \dot{q_1} \\ \dot{q_2} \\ \dot{q_3} \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 0 & -\omega_1 & -\omega_2 & -\omega_3 \\ \omega_1 & 0 & \omega_3 & -\omega_2 \\ \omega_2 & -\omega_3 & 0 & \omega_1 \\ \omega_3 & \omega_2 & -\omega_1 & 0 \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{pmatrix}$

Une écriture plus compacte est possible :

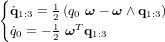
$\begin{cases} \dot{\bold q}_{1:3} = \frac{1}{2} \left(q_0 \ \boldsymbol\omega - \boldsymbol\omega \wedge \bold q_{1:3} \right) \\ \dot{q}_0 = -\frac{1}{2} \ \boldsymbol\omega^T \bold{q}_{1:3} \end{cases}$

Contrairement aux angles d'Euler, les quaternions ne présentent pas de singularité géométrique. L'équation cinématique exprimée avec les quaternions ne possède pas de fonctions trigonométriques, ce qui rend les quaternions parfaitement adaptés aux calculs à bord réalisés en temps réel. Ainsi, les algorithmes de détermination d'attitude modernes sont généralement décrits en termes de quaternions.