Les points de Lagrange

Auteur: Valérie Ciarletti

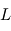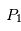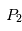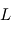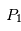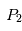Dans le cas particulier du problème à trois corps, on s'intéresse ici au mouvement d'un corps 'test' de masse négligeable qui subit l'attraction de deux corps plus massifs $\ P_1$ et $\ P_2$ . Le fait que la masse du corps soit négligeable permet de considérer que les mouvements de $\ P_1$ et $\ P_2$ ne sont pas perturbés par la présence de .

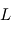Pour simplifier la présentation du problème, nous allons nous restreindre au cas où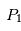 $\ P_1$ est l'étoile et 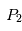$\ P_2$ une planète, beaucoup moins massive, est en orbite circulaire autour de son étoile.

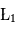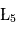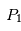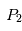Le mathématicien Joseph-Louis Lagrange (1772) étudie ce problème. Il montre qu'il existe 5 points, dits de Lagrange (notés $\L_1$ à $\L_5$ ), pour lesquels les forces d'attraction de $\ P_1$ et $\ P_2$ se combinent de façon à ce que le corps "test" 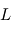de masse négligeable ait la même période de révolution que les deux autres corps et les suive donc dans leur mouvement autour du centre de gravité de 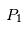$\ P_1$ et $\ P_2$ .

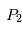En contradiction apparente avec les résultats obtenus dans le cadre du problème à deux corps, on peut trouver des corps de masse négligeable qui ont donc une période de révolution égale à celle de la planète mais qui ne sont pas sur la même orbite.

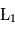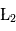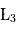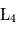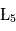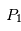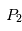On montre que les points $\L_1$ , $\L_2$ et $\L_3$ (parfois appelés Points d'Euler) correspondent à des positions instables alors que les points $\L_4$ et $\L_5$ correspondent à des positions stables. Les positions de ces deux derniers points ne dépendent pas des masses des points $\ P_1$ et $\ P_2$ . Dans le cas, du système Soleil/Jupiter, ce sont au voisinage de ces points que se trouvent les nombreux astéroïdes troyens qui suivent (ou précèdent) la révolution de la Terre autour du Soleil. D'autres planètes du système solaire sont suivies ou précédées également par des petits corps troyens (la liste des troyens détectés à ce jour dans notre système solaire est disponible sur le site du Minor Planet Center )

Visualisation des points de Lagrange

Positions des points de Lagrange pour le système étoile-planète (représentées en rouge). Les points de Lagrange stables sont représentés en vert, les points instables en bleu.

Appliquette Système Solaire

Etude par simulation numérique des points de Lagrange

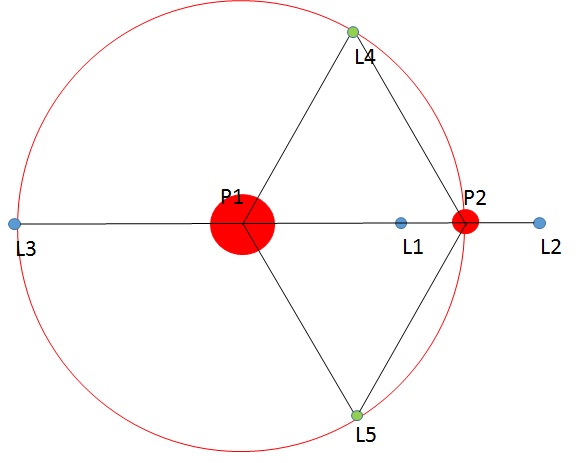
Vous allez utiliser l'appliquette pour visualiser les points de Lagrange (astéroïdes Troyens) stables et instables d'un système étoile-planète.

Attention : Cette appliquette utilise un système d'unités arbitraire pour les distances, vitesses, masses et temps de façon à ce que les valeurs numériques restent inférieures à un millier.

Question 1)

Choisissez pour commencer le système 'astéroïdes Troyens' proposé par l'appliquette

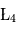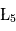Laissez évoluer ce système, sans modifier les conditions initiales, jusqu'à 100 unités de temps pour vérifier que les deux petits corps positionnés aux points de Lagrange $\L_4$ et $\L_5$ ont bien la même période de révolution autour de l'étoile que la planète.

Vérifiez qu'initialement les trois corps ont des vitesses très voisines.

Modifiez la masse de l'un des astéroides (de 0.001 à 1 par exemple) et observer le changement qui apparait après un temps suffisamment long d'environ 50 unités. Expliquez ce qui se passe et proposez une explication.

Solution

Question 2)

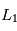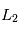Vous allez maintenant utiliser l'appliquette afin d'étudier les mouvements d'un corps de masse négligeable au voisinage des points de Lagrange instables L_1 et L_2 (situés de part et d'autre de la planète sur l'axe entre la planète et l'étoile).

Créez pour commencer un système à deux corps avec les valeurs numériques suivantes pour l'étoile et la planète : 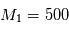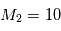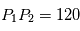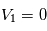M_1=500 , M_2=10 , P_1P_2=120 , V_1=0 . Trouver (en tâtonnant) une valeur de la vitesse initiale qui permet d'avoir une orbite quasi-circulaire pour la planète. Vérifiez que l'orbite de 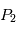P_2 autour de est voisine d'une orbite circulaire.

Solution

Question 3)

Etude des points de Lagrange 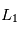L_1 et L_2

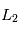
Vous allez maintenant ajouter à ce système un troisième corps de masse très faible aux positions qui correspondent aux points de Lagrange 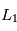L_1 et L_2 .

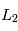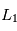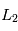On peut montrer par méthode perturbative que les positions de L_1 et L_2 par rapport au centre de masse du système étoile-planète sont données par les développements limités suivants:

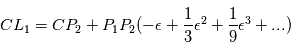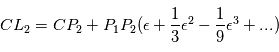
$CL_1=CP_2 +P_1P_2(-\epsilon+\frac{1}{3}\epsilon^2+\frac{1}{9}\epsilon^3+...)$ et $CL_2=CP_2 +P_1P_2(\epsilon+\frac{1}{3}\epsilon^2-\frac{1}{9}\epsilon^3+...)$

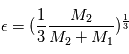
avec $\epsilon=({\frac{1}{3}\frac{M_2}{M_2+M_1}})^\frac{1}{3}$

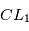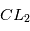Calculer la valeur de CL_1 et CL_2 pour la configuration que vous allez simuler.

Solution

Question 4)

Ajoutez dans le système à deux corps, un point de masse négligeable sur l'axe étoile-planète à la position 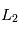L_2 que vous avez précédemment calculée. Donnez à ce petit corps une vitesse initiale quelconque et observez ce que donne la simulation. Etudiez, en prenant quelques valeurs de vitesse différentes, l'impact sur la trajectoire du petit corps. Trouvez une valeur de vitesse initiale qui permet à ce petit corps d'avoir une vitesse angulaire proche de celle de la planète en révolution autour du soleil (au moins pendant une courte durée)

Aide

Question 5)

Reprennez les questions précédentes pour la position 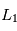L_1 que vous avez calculée.

Solution