Angles d'Euler

Auteur: Gary Quinsac

Séquence d'Euler pour les paramètre orbitaux

La séquence d'Euler (3-1-3) correspond aux paramètres orbitaux habituellement utilisés pour un satellite en orbite terrestre : le nœud ascendant ( $\Omega$ ), l'inclinaison (

) et l'anomalie vraie ( $\nu$ ).

Crédit : Gary Quinsac

Présentation des angles d'Euler

Les angles d'Euler sont les angles introduits par Leonhard Euler pour décrire l'orientation d'un solide. Ils peuvent être utilisés pour définir l'orientation d'un référentiel par rapport à un autre. On obtient une rotation en faisant varier l'un des trois angles d'Euler et une séquence de 3 rotations est suffisante pour décrire n'importe quelle transformation. La première rotation est effectuée selon n'importe quel axe, tandis que les deux suivantes ne peuvent jamais être effectuées autour d'un axe utilisé par la rotation précédente. Au total, 12 jeux d'angles d'Euler existent : (1,2,1), (1,2,3), (1,3,1), (1,3,2), (2,1,2), (2,1,3), (2,3,1), (2,3,2), (3,1,2), (3,1,3), (3,2,1), (3,2,3). L'ordre des rotations et la valeur des angles ne sont pas uniques et sont sujets à des singularités mathématiques.

Exemples

Appliquette interactive

Une appliquette interactive est disponible ici. Elle permet de visualiser dans l'espace les séquences d'Euler qui sont introduites dans cette section à titre d'exemple.

La séquence d'Euler la plus connue, nommée d'après lui, est la séquence (3,1,3). Elle a notamment été utilisée pour étudier le mouvement gyroscopique avec les trois rotations successives :
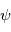- La précession $\psi$ , autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).
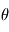- La nutation $\theta$ , autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).
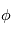- La giration $\phi$ , ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
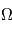Cette séquence peut également être utilisée pour décrire les paramètres orbitaux d'un satellite par rapport au référentiel inertiel centré sur la Terre. La première rotation correspond alors à l'angle du noeud ascendant, , autour de l'axe . La deuxième rotation est l'inclinaison, 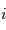, autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie, 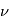, autour de la normale à l'orbite.
La séquence (3-1-2) est souvent utilisée pour décrire l'orientation d'un satellite par rapport au référentiel orbital.
- La première rotation correspond au lacet, autour du nadir.
- La suivante est le roulis, autour de l'axe $\bold X$ du satellite.
- La dernière est le tangage.

Les angles d'Euler décrivent une rotation unique, ce qui est généralement un avantage par rapport à la MCD. Cependant, à une orientation donnée correspondent plusieurs jeux d'angles d'Euler.

De la séquence d'Euler à la MCD

Quelle que soit la séquence d'Euler, la MCD peut facilement être obtenue en multipliant les matrices de rotation élémentaires. Soit la séquence particulière suivante, décrivant l'orientation du référentiel 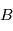par rapport au référentiel :

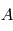$[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$

$[T]_{B|A} = [T(\theta_1)]_1 [T(\theta_2)]_2 [T(\theta_3)]_3$ , donc : $[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}$

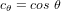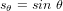Nous avons utilisé les notations $c_{\theta} = cos \ \theta$ et $s_{\theta} = sin \ \theta$ .

Limites de cette représentation

D'une manière générale, les angles d'Euler déterminent une orientation unique, ce qui est un avantage sur la MCD. Des singularités apparaissent lorsque le deuxième angle d'Euler aligne les premier et troisième axes de rotation. Dans ce cas, cette description d'attitude à 3 degrés dégénère en une description à seulement 2 degrés de liberté. Cette condition est réalisée lorsque l'angle vaut 90 et 270 degrés pour les 6 rotations où les premier et troisième axes sont différents, et lorsque l'angle vaut 0 et 190 degrés pour les 6 rotations où les premier et troisième axes sont identiques.