Matrice du cosinus directeur

Auteur: Gary Quinsac

La façon la plus évidente de donner l'orientation d'un référentiel par rapport à un autre est d'exprimer leurs vecteurs de base dans l'autre repère.

Changement de repère en 2D

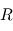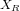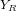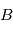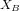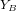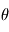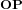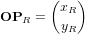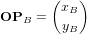Une introduction simple à ce changement de repère peut être faite en 2D. Prenons un référentiel , avec les axes X_R et Y_R , incliné par rapport à un référentiel , d'axes X_B et Y_B , d'un angle $\theta$ . Le vecteur $\bold {OP}$ peut être exprimé dans ces deux systèmes sous forme matricielle : ${\bold {OP}}_R = \binom{x_R}{y_R}$ et ${\bold {OP}}_B = \binom{x_B}{y_B}$ .

La relation entre les deux systèmes de coordonnées peut être décrite par une matrice de cosinus directeur (MCD), ou matrice de rotation, variant avec 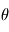$\theta$ . Cette matrice transforme le vecteur 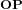$\bold{OP}$ du premier référentiel 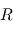vers le second .

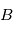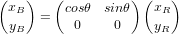
$\binom{x_B}{y_B} = \begin{pmatrix} cos \theta & sin \theta \\ 0 & 0 \end{pmatrix} \binom{x_R}{y_R}$

Les éléments de la MCD correspondent aux produits scalaires des vecteurs de base. Le produit scalaire entre deux vecteurs unitaires correspond au cosinus de l'angle formé par ces vecteurs.

Appliquette interactive

Une appliquette interactive est disponible ici. Elle revient sur le changement de repère en 2D en permettant de projeter les coordonnées d'un point dans un référentiel en rotation par rapport à un autre.

Généralisation à l'espace à 3 dimensions

En 3 dimensions la MCD est une matrice de passage 3x3. L'expression d'un vecteur 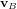$\bold v_B$ dans 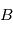à partir de son expression 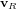$\bold v_R$ dans 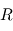s'écrit :

$\bold v_B = [T]_{B|R} \bold v_R$ avec $[T]_{B|R} = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_x \cdot \bold R_y & \bold B_x \cdot \bold R_z \\ \bold B_y \cdot \bold R_x & \bold B_y \cdot \bold R_y & \bold B_y \cdot \bold R_z \\ \bold B_z \cdot \bold R_x & \bold B_z \cdot \bold R_y & \bold B_z \cdot \bold R_z \end{pmatrix}$

On dit que la MCD décrit l'orientation de 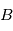par rapport à 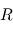. On l'appelle également matrice de rotation ou matrice de transformation des coordonnées de 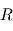vers .

Rotations élémentaires

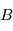Trois rotations élémentaires de 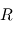autour de chacun de ses trois axes se retrouvent décrites par les matrices de rotation suivantes :

$[T(\theta_1)]_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_{\theta_1} & s_{\theta_1} \\ 0 & -s_{\theta_1} & c_{\theta_1} \end{pmatrix}$ , $[T(\theta_2)]_2 = \begin{pmatrix} c_{\theta_2} & 0 & -s_{\theta_2} \\ 0 & 1 & 0 \\ s_{\theta_2} & 0 & c_{\theta_2} \end{pmatrix}$ et $[T(\theta_3)]_3 = \begin{pmatrix} c_{\theta_3} & s_{\theta_3} & 0 \\ -s_{\theta_3} & c_{\theta_3} & 0 \\ 0 & 0 & 1 \end{pmatrix}$

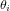où $[T(\theta_i)]_i$ indique une rotation d'angle $\theta_i$ autour du i-ème axe du référentiel fixé sur le corps.

Propriétés de la MCD

La MCD est une matrice orthogonale, ce qui signifie que son inverse est égal à sa transposée :

$[T]^{-1} = [T]^T$ et [T][T]^T = [I] = [T]^T[T]

$\bold v_R = [T]_{R|B}^T \bold v_B = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_y \cdot \bold R_x & \bold B_z \cdot \bold R_x \\ \bold B_x \cdot \bold R_y & \bold B_y \cdot \bold R_y & \bold B_z \cdot \bold R_y \\ \bold B_x \cdot \bold R_z & \bold B_y \cdot \bold R_z & \bold B_z \cdot \bold R_z \end{pmatrix}$

Les transformations successives entre référentiels peuvent être déterminées par une série de multiplications matricielles. Par exemple, la transformation du référentiel inertiel au référentiel du satellite peut être décomposée de la manière suivante : transformation du référentiel inertiel au référentiel fixé sur la Terre multipliée par la transformation du référentiel fixé sur la Terre au référentiel orbital, le tout multiplié par la transformation du repère orbital au repère du satellite.

$[T]_{sat|inertiel} = [T]_{sat|orbite} [T]_{orbite|Terre} [T]_{Terre|inertiel}$

Limitations de cette représentation

Malgré certains avantages, la MCD n'est pas toujours la représentation la plus adaptée. Elle utilise 9 paramètres pour décrire une orientation, parmi lesquels seulement 3 sont indépendants.