Représentation 3D

Auteur: Gary Quinsac

Afin de s'affranchir du problème de singularité rencontré avec les angles d'Euler, une représentation de l'attitude composée de 4 éléments est introduite sous le nom de quaternion (dont les éléments sont appelés paramètres d'Euler). Cette construction mathématique est présentée plus en détail dans la partie suivante.

Présentation des quaternions

Considérons l'axe fixe de la rotation présentée dans le théorème d'Euler, ou vecteur propre $\bold e$ . C'est un vecteur unité possédant les mêmes composantes dans les référentiels de départ et d'arrivée : $\bold e_r = \bold e_b$ . 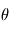Ainsi, 4 grandeurs sont requises pour décrire de façon non-ambigüe l'orientation par rapport à un référenciel : les 3 composantes de $\bold e$ et l'angle de la rotation, $\theta$ .

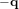Les quaternions sont une combinaison de ces éléments disposés dans un vecteur de 4 éléments $\bold q$ . Le quaternion contient la même information qu'une MCD à 9 éléments, tout en s'affranchissant des problèmes de singularité rencontrés avec les angles d'Euler. Ils sont à la fois compacts et une représentation efficace de l'orientation pour la détermination d'attitude. Une même rotation est représentée par les quaternions $\bold q$ et $- \bold q$ . On note également que les quatre paramètres d'Euler ne sont pas indépendants, mais contraints par la relation suivante :

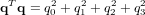
$\bold q^T \bold q = q_0^2 + q_1^2 + q_2^2 + q_3^2$

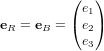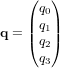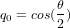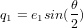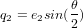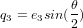Pour le vecteur propre $\bold e_R = \bold e_B = \begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix}$ , les paramètres d'Euler sont : $\bold q = \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{pmatrix}$ , avec $q_0 = cos({\theta \over 2})$ , $q_1 = e_1 sin({\theta \over 2})$ , $q_2 = e_2 sin({\theta \over 2})$ et $q_3 = e_3 sin({\theta \over 2})$ .

Des quaternions à la MCD

De la même façon que l'on peut exprimer la MCD en fonction des angles d'Euler, elle peut être paramétrée en fonction d'un quaternion de la manière suivante :

$[T]_{B|R} = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}$

Propriétés des quaternions

Il s'agit maintenant d'expliquer comment un quaternion vivant dans 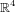$\mathbb{R}^4$ peut opérer sur un vecteur vivant lui dans 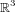$\mathbb{R}^3$ . Notons tout d'abord qu'un vecteur est un quaternion pur dont la partie réelle est nulle. L'opérateur 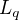décrivant une rotation s'exprime avec le quaternion unitaire 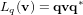$\bold q$ : $L_q(\bold v) = \bold q \bold v \bold q^*$ . Le vecteur ainsi obtenu conserve la longueur du vecteur initial, comme le fait une rotation. Cet opérateur se développe de la manière suivante :

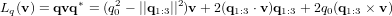
$L_q(\bold v) = \bold q \bold v \bold q^* = (q_0^2 - ||\bold q_{1:3}||^2) \bold v + 2(\bold q_{1:3} \cdot \bold v) \bold q_{1:3} + 2 q_0 (\bold q_{1:3} \times \bold v)$

Afin de comprendre cette expression il est nécessaire d'avoir compris la partie suivante qui s'intéresse à l'algèbre des quaternions.
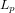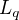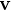Les séquences de rotation peuvent facilement être décrites par une multiplication des quaternions représentant les rotations successives. Soient les quaternions $\bold p$ et $\bold q$ décrivant respectivement les opérateurs et . Le premier opérateur est appliqué au vecteur $\bold u$ pour obtenir le vecteur $\bold v$ , puis le second est appliqué à 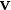$\bold v$ pour obtenir 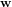$\bold w$ . La composition des opérateurs 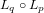$L_q \circ L_p$ s'écrit :

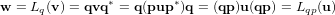
$\bold w = L_q(\bold v) = \bold q \bold v \bold q^* = \bold q (\bold p \bold u \bold p^*) \bold q = (\bold q \bold p) \bold u (\bold q \bold p) = L_{qp}(\bold u)$

Avantage des quaternions

Un avantage inhérent à cette représentation est que les équations de la cinématique deviennent purement algébriques et ne contiennent plus de fonctions trigonométriques.