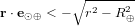Pression de radiation solaire

Auteur: Gary Quinsac

Géométrie du couple de pression de radiation solaire

images/geometrie-pression-radiation-solaire.png

Géométrie du couple de pression de radiation solaire. Chaque face du satellite exposée au Soleil subit une force qui, si elle est désaxée par rapport au centre de masse, engendre un couple.

Crédit : Gary Quinsac

La pression de radiation solaire est la source dominante de couples perturbateurs dans l'espace interplanétaire (absence de traînée atmosphérique, faibles champs de gravité et magnétique). Même en orbite basse, on a pour habitude de considérer qu'il est dominant à des altitudes supérieures à 800 km. Il est important de noter que si le Soleil n'est pas l'unique source de radiation (il y a notamment l'albédo de la Terre et de la Lune, les rayons cosmiques...), il est de loin la plus importante. Le Soleil émet des photons, mais également des protons et des électrons (vent solaire). L'interaction entre la lumière du Soleil et la surface du satellite est habituellement modélisée comme une force de pression exercée sur un objet.

On modélise la surface du satellite comme une collection de 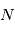surfaces d'aire 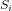S_i , dont la normale orientée vers l'extérieur est notée 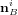$\bold n_B^i$ dans le référentiel du satellite et de coefficient de réflexion 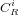C_R^i (on lui attribue généralement une valeur de 0,6 pour un petit satellite).

Le vecteur allant du satellite au Soleil dans le référentiel du satellite s'écrit 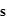vecteur(s) . L'angle entre ce vecteur et et la normale à la i^ème surface s'écrit alors :

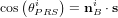
$\textup{cos} \left(\theta_{PRS}^i \right) = \bold n_B^i \cdot \bold s$

La force de pression de radiation solaire exercée sur une surface peut alors s'exprimer de la manière suivante :

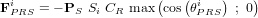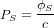
$\bold F_{PRS}^i = - \bold P_S \ S_i \ C_R \ \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)$ avec $P_S = \frac{\phi_S}{c}$

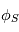où $\phi_S$ (en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et 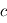(en m/s) est la vitesse de la lumière.

La différence entre les positions des centres de pression solaire et de masse aboutit à un couple de radiation solaire. Une telle différence dépend des surfaces éclairées, de l'incidence des rayons lumineux et de la répartition de la masse à l'intérieur du satellite. On note 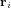$\bold r_i$ le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la i^ème surface. Le couple de radiation solaire s'écrit alors :

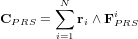
$\bold C_{PRS} = \sum_{i=1}^{N}{\bold r_i \wedge \bold F_{PRS}^i}$

Complément : coefficients de réflexion

Afin de gagner en précision, il est possible de détailler le coefficient de réflexion en une somme de trois coefficients dont le résultat vaut 1 :

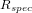le coefficient de réflexion spéculaire $R_{spec}$ ;
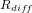le coefficient de réflexion diffuse $R_{diff}$ ;
le coefficient d'absorption $R_{abs}$ .

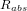La force de pression de radiation sur la i^ème surface s'exprime alors :

$\bold F_{PRS}^i = -P_S \ S_i \left[ 2 \left( \frac{R_{diff}^i}{3} + R_{spec}^i \ \textup{cos} \left(\theta_{PRS}^i \right) \right) \bold n_B^i + \left( 1-R_{spec}^i \right) \bold s \right] \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)$

Complément : irradiance solaire

L'irradiance solaire représente la quantité d'énergie solaire reçue par une surface de 1 m² située à une certaine distance r du Soleil et exposée perpendiculairement. Afin de la calculer, il faut considérer la conservation de l'énergie rayonnée dans l'espace et écrire :

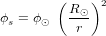
$\phi_s = \phi_{\odot} \ \left( \frac{R_{\odot}}{r} \right)^2$

avec 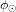$\phi_{\odot}$ le flux émis à la surface du Soleil et 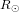$R_{\odot}$ le rayon du Soleil. 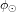$\phi_{\odot}$ est estimé en appliquant la loi de Stefan-Boltzmann au Soleil considéré comme un corps noir :

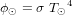
$\phi_{\odot} = \sigma \ {T_{\odot}}^4$

avec 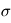$\sigma$ la constante de Stefan-Boltzmann et 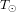$T_{\odot}$ la température thermodynamique du corps noir. À la distance moyenne Terre-Soleil (1 UA) l'irradiance solaire (ou constante solaire) vaut 1362 W.m^-2.

Zone d'ombre

Afin de simuler la pression de radiation solaire, il ne faut pas oublier les zones d'ombres dans lesquelles le satellite peut se retrouver. Par exemple, en orbite basse autour de la Terre, un satellite peut passer une partie importante de son orbite caché des rayons du Soleil. L'approche la plus simple est de considérer que l'ombre de la Terre est une projection cylindrique du diamètre de la Terre le long de l'axe Soleil-Terre. Sur cette figure on remarque qu'en faisant le produit scalaire de vecteur unitaire 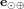$\bold e_{\odot \oplus}$ (Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :

$\bold r \cdot \bold e_{\odot \oplus} < - \sqrt{r^2 - R_{\oplus}^2}$