Bases de la dynamique

Auteur: Gary Quinsac

Maintenant que nous nous tournons vers la dynamique d'attitude, il est important de bien différencier le mouvement de rotation d'un système du mouvement de son centre d'inertie. Nous allons nous concentrer sur le cas d'un corps rigide.

Force / Moment / Couple

Une force représente l'action d'un corps sur un autre. En revanche le moment d'une force par rapport à un point décrit l'aptitude de cette force à faire tourner un système autour de ce point. Le moment 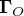$\bold \Gamma_O$ de la force 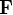$\bold F$ par rapport à au point 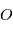est défini par :

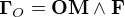
$\bold \Gamma_O = \bold{OM} \wedge \bold F$

On parle de couple lorsqu'un ensemble de forces a une résultante nulle sur un système (leur somme vaut 0) alors que le moment résultant par rapport à un point 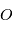est non nul. Dans ce cas, il est possible de montrer que le moment global d'un tel couple par rapport à n'importe quel point est égal au produit vectoriel caractéristique du couple :

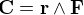
$\bold C= \bold{r} \wedge \bold F$

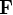où $\bold r$ est le vecteur allant du centre de gravité du système au point d'application de la force $\bold F$ . Si, pour un corps solide sans contraine, une force va accélérer son centre de masse, un couple aura lui pour effet d'induire un mouvement de rotation autour du centre de masse.

Remarque

On parle de couple pur lorsqu'une paire de forces d'intensité égale mais de directions opposées agissent à distance.

Propriétés d'inertie

Lorsque l'on parle du mouvement d'un solide autour de son centre d'inertie, il nous faut définir le tenseur d'inertie. Il s'exprime ainsi :

$[I] = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{n}{m_i \left(y_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & -\sum_{i=1}^{n}{m_i \ x_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ z_i} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+y_i^2 \right)} \end{pmatrix}$ ,

Les éléments diagonaux de ces expressions sont les moments d'inertie du solide par rapport aux divers axes, et les autres éléments sont les produits d'inertie. Les propriétés inertielles d'un solide sont donc totalement décrites par sa masse, la localisation de son centre d'inertie (ou centre de masse), et par les moments et produits d'inertie définis par rapport à des axes de références en un point particulier. Tous les solides ont un jeu d'axes principaux d'inertie dont l'origine se trouvent en son centre de masse et qui annule les produits d'inertie, rendant diagonale la matrice d'inertie.

Appliquette interactive

Une appliquette interactive est disponible ici. Elle illustre l'importance du choix des axes d'inertie dans le calcul de la matrice d'inertie.

Moment cinétique

L'analogie avec l'étude du centre de masse est une nouvelle fois possible. Le moment linéaire d'un corps solide, produit de la masse de ce corps par la vitesse de son centre de masse, est appelé quantité de mouvement, 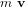$m \ \bold v$ . Considérons un système matériel qui est la somme de 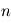masses ponctuelles. Le moment angulaire, ou moment cinétique, par rapport à un point 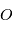est le moment de la quantité de mouvement $\bold p$ par rapport à ce point :

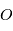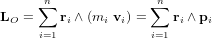
$\bold L_O = \sum_{i=1}^{n}{\bold r_i \wedge \left( m_i \ \bold v_i \right)} = \sum_{i=1}^{n}{\bold r_i \wedge \bold p_i}$

On a également pour habitude d'exprimer le moment angulaire à partir de la matrice de moment d'inertie [I] et de la vitesse angulaire 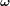$\boldsymbol\omega$ :

$\bold L = [I] \ \boldsymbol\omega$

Le passage de l'une à l'autre des expressions se fait en considérant que :

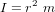$I = r^2 \ m$ est le moment d'inertie d'une masse ponctuelle,
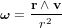$\boldsymbol\omega = \frac{\bold r \wedge \bold v}{r^2}$ est le moment angulaire de la particule par rapport à l'origine.

Rappel

Cours sur le principe fondamental de la dynamique