| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Exercices : Représentation d'attitude |
Difficulté : ☆
On souhaite montrer que la MCD est une matrice orthonormale, c'est-à-dire que ![[T] \ [T]^T = [I] = [T]^T \ [T]](../pages_nanosats/equations_nanosats-setester/equation1.png) .
.
Soit la MCD ![[T]_{B|A}](../pages_nanosats/equations_nanosats-setester/equation2.png) entre deux référentiels orthogonaux décrits par les vecteurs unitaires
entre deux référentiels orthogonaux décrits par les vecteurs unitaires 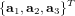 et
et 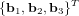 :
:
![\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = [T]_{B|A} \ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation5.png)
Ecrire le vecteur transposé de 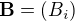 .
.
Calculer le produit 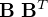 et conclure.
et conclure.
Difficulté : ☆
Cet exercice a pour but de démontrer l'expression de la MCD à partir d'une certaine séquence d'angles d'Euler. On reprend la notation du cours en nommant 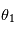 ,
, 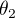 et
et 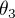 les trois angles d'Euler.
les trois angles d'Euler.
Démontrer qu'en choisissant la séquence ![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation15.png) afin de passer du référentiel
afin de passer du référentiel 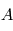 au référentiel
au référentiel 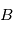 , on obtient bien la formule présentée dans le cours :
, on obtient bien la formule présentée dans le cours :
![[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation18.png)
Considérons maintenant la séquence suivante : ![[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2](../pages_nanosats/equations_nanosats-setester/equation20.png) . Exprimer la MCD associée à cette séquence.
. Exprimer la MCD associée à cette séquence.
Difficulté : ☆
Considérons la séquence de rotations fixées par rapport à un satellite allant du référentiel 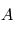 au référentiel
au référentiel 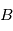 :
:
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-setester/equation24.png)
Les quaternions associés à ces rotations sont :
![[T(\theta_1)]_1 = \begin{pmatrix} sin(\theta_1 / 2) \\ 0 \\ 0 \\ cos(\theta_1 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation25.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ sin(\theta_2 / 2) \\ 0 \\ cos(\theta_2 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation26.png) ,
, ![[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ 0 \\ sin(\theta_3 / 2) \\ cos(\theta_3 / 2) \end{pmatrix}](../pages_nanosats/equations_nanosats-setester/equation27.png)
Montrer que les angles d'Euler de cette séquence de rotation sont reliés aux quaternions de la manière suivante :
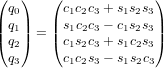
où 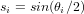 et
et 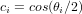
Vérifier que pour des angles infinitésimaux on obtient un quaternion très simple.