Exercices : Equations du mouvement

Auteur: Gary Quinsac

Cinématique d'attitude avec la MCD

Difficulté : ☆☆

On souhaite démontrer l'équation de la cinématique exprimée avec la MCD.

$\frac{d}{dt}([T]) = -[\Omega] \ [T]$ avec $[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}$ et $[T] = \begin{pmatrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{pmatrix}$

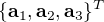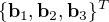Soit la MCD [T] entre deux référentiels orthogonaux décrits par les vecteurs unitaires $\{\bold{a}_1, \bold{a}_2, \bold{a}_3\}^T$ et $\{\bold{b}_1, \bold{b}_2, \bold{b}_3\}^T$ .

Question 1)

Rappeler la propriété principale de la MCD [T] .

Aide

Question 2)

Exprimer la dérivée de l'équation exprimant un vecteur du référentiel (B) en fonction d'un vecteur du référentiel (A).

Aide Aide

Question 3)

Obtenir l'équation de la cinématique exprimée avec la MCD.

Aide Aide

Question 4)

À partir de l'équation de la cinématique que nous venons de démontrer, exprimer les différentes coordonnées du vecteur vitesse angulaire.

Aide

Auteur: Gary Quinsac

Cinématique d'attitude avec les angles d'Euler

Difficulté : ☆☆

Cet exercice cherche à établir les équations de la cinématique pour certaines représentations d'Euler. Les premières questions considèrent la séquence d'Euler permettant de passer du référentiel (A) au référentiel (B) suivante : $[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$ .

Question 1)

Ecrire les trois vecteurs vitesse angulaire correspondant à chaque transformation élémentaire en fonction des dérivées des angles d'Euler.

Aide

Question 2)

Exprimer le vecteur de vitesse angulaire 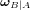${\boldsymbol\omega}_{B|A}$ en fonction des vecteurs de vitesse angulaire précédents.

Question 3)

Reformuler cette équation afin de faire apparaître les vecteurs de base des différents repères.

Question 4)

Exprimer les vecteurs de base des repères 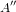A'' et 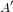en fonction de ceux de (B).

Question 5)

Montrer la relation de la cinématique pour cette séquence d'Euler :

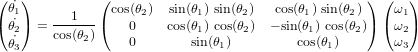
$\begin{pmatrix} \dot{\theta_1} \\ \dot{\theta_2} \\ \dot{\theta_3} \end{pmatrix} = \frac{1}{\textup{cos}(\theta_2)} \begin{pmatrix} \textup{cos}(\theta_2) & \textup{sin}(\theta_1) \ \textup{sin}(\theta_2) & \textup{cos}(\theta_1) \ \textup{sin}(\theta_2) \\ 0 & \textup{cos}(\theta_1) \ \textup{cos}(\theta_2) & -\textup{sin}(\theta_1) \ \textup{cos}(\theta_2) \\ 0 & \textup{sin}(\theta_1) & \textup{cos}(\theta_1) \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}$

Question 6)

Considérons maintenant la séquence suivante : $[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2$ . Exprimer alors l'équation de la cinématique.

Aide

Auteur: Gary Quinsac

Cinématique d'attitude avec les quaternions

Difficulté : ☆☆

Il est maintenant question de démontrer l'équation de la cinématique avec les quaternions.

Question 1)

Reprendre la forme de l'équation de la cinématique trouvée dans la dernière question du premier exercice sur les équations du mouvement :

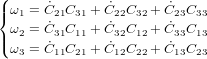
$\begin{cases} \omega_1 = \dot C_{21} C_{31} + \dot C_{22} C_{32} + \dot C_{23} C_{33} \\ \omega_2 = \dot C_{31} C_{11} + \dot C_{32} C_{12} + \dot C_{33} C_{13} \\ \omega_3 = \dot C_{11} C_{21} + \dot C_{12} C_{22} + \dot C_{13} C_{23} \end{cases}$

Substituer les coefficients de la MCD par leur forme avec les quaternons.

Aide

Question 2)

Exprimer la dérivée de l'équation contraignant les quaternions.

Aide

Question 3)

Regrouper ces 4 équations sous forme matricielle.

Question 4)

Utiliser une propriété remarquable de la matrice de quaternion obtenue dans la questions précédente pour exprimer la dérivée du quaternion.

Aide

Question 5)

Réécrire l'équation afin d'obtenir l'équation de la cinématique avec les quaternions.