Exercices : Lois de commande

Auteur: Gary Quinsac

Ressort

Crédit : Gary Quinsac

Auteur: Gary Quinsac

Étude d'un ressort

Difficulté : ☆

Cet exercice a pour but de vous entraîner à utiliser les transformations de Laplace pour résoudre une équation différentielle.

Considérons une masse m accrochée à un ressort de constante de rappel K. On mesure le déplacement vertical de la masse, provoqué par une stimulation u(t), par la grandeur x. L'installation est illustrée par cette figure.

Question 1)

Quelle est l'équation de déplacement de la masse ?

Question 2)

On veut étudier le cas d'une stimulation impulsionnelle. Que devient u(t) ?

Question 3)

Exprimer la fonction de transfert du système.

Aide Aide

Question 4)

Effectuer la transformée de Laplace inverse de la fonction de transfert afin d'exprimer le déplacement issu d'une stimulation impulsionnelle dans le domaine temporel.

Question 5)

Supposons maintenant que la stimulation n'est plus impulsionnelle mais une rampe 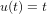u(t) =t . Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :

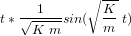
$t \ast \frac{1}{\sqrt{K \ m}} sin(\sqrt{\frac{K}{m}} \ t)$

Passer par la transformée de Foutier.

Aide

Auteur: Gary Quinsac

Représentation de la boucle de contrôle d'attitude

Nous allons retrouver la fonction de transfert de la boucle de contrôle d'attitude :

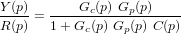
$\frac{Y(p)}{R(p)} = \frac{G_c(p) \ G_p(p)}{1+G_c(p) \ G_p(p) \ C(p)}$

On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, G_c(p) le contrôleur, E(p) l'erreur, G_p(p) le matériel à contrôler et C(p) la dynamique des capteurs.

Question 1)

Exprimer le signal de sortie en fonction du signal de contrôle.

Question 2)

Sachant que l'on considère que les perturbations sont nulles, exprimer le signal de contrôle en fonction de l'erreur.

Question 3)

Appliquer la même approche pour trouver l'expression de l'erreur.

Question 4)

Réorganiser les résultats précédents afin de retrouver l'expression de la fonction de transfert.