| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Loi binomiale |
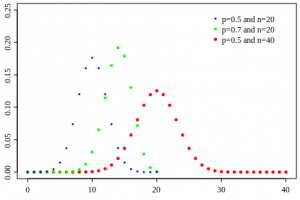
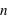 ) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (
) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (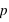 ). Pour le même nombre de lancers
). Pour le même nombre de lancers 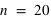 , le pic est à 14 avec un probabilté
, le pic est à 14 avec un probabilté 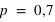 et seulement 10 avec
et seulement 10 avec 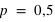 . Pour
. Pour 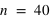 et
et 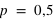 , le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de
, le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de 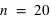 et
et 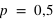 , lorsque
, lorsque 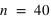 , la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque
, la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque 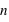 tend vers l'infini.
tend vers l'infini.
Les lois n'ayant que deux évènements sont les plus simples mais aussi les plus utilisées. L'ensemble univers de ces lois de probabilités n'étant composé que de deux événements, il s'agit d'une variable discrète. Les événements peuvent être représentés par 0 et 1. Par exemple le jet d'une pièce suit ce type de lois : 0 étant par convention "pile" et 1 "face". L'évènement 0 a une probabilité notée 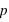 alors que l'événement 1 a une probabilité notée
alors que l'événement 1 a une probabilité notée 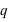 . Toujours, dans le cas d'une pièce de monnaie,
. Toujours, dans le cas d'une pièce de monnaie, 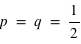 . De manière générale,
. De manière générale, 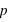 et
et 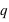 n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas
n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas 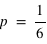 et
et 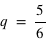 . De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité
. De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité 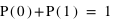 donc
donc 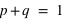 et
et 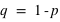 . Les lois à deux événements ne dépendent donc que d'un paramètre,
. Les lois à deux événements ne dépendent donc que d'un paramètre, 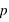 .
.
En compléxifiant la loi vue ci-dessus, il est possible de créer la loi binomiale. Cette dernière s'intéresse aux résultats de plusieurs lancers d'une expérience n'ayant que deux événements possibles. Par exemple, lorsqu'une pièce est lancée 20 fois de suite, quelle est la probabilité d'avoir 10 faces ou 3 piles ou même 20 faces de suite ? La loi binomiale dépend donc de deux paramètres : la propabilité 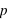 de la loi à deux événements et le nombre de répétition de cette loi,
de la loi à deux événements et le nombre de répétition de cette loi, 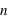 . Son ensemble univers est constitué de toutes les séries possibles de
. Son ensemble univers est constitué de toutes les séries possibles de 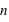 répétitions de la loi à deux évènements. Le nombre d'événements vaut donc
répétitions de la loi à deux évènements. Le nombre d'événements vaut donc 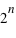 car à chaque répétition (
car à chaque répétition (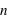 en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne
en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne 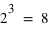 évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté
évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté 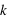 , et de 1, noté
, et de 1, noté 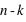 . Par définition la probabilité de 0 vaut
. Par définition la probabilité de 0 vaut 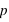 et celle de 1 vaut
et celle de 1 vaut 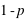 . Donc la probabilité d'un évènement est
. Donc la probabilité d'un évènement est 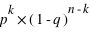 . L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer
. L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer 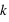 évènements 0 sur
évènements 0 sur 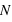 lancers. Pour cela, il suffit de remarquer que pour un nombre
lancers. Pour cela, il suffit de remarquer que pour un nombre 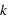 d'événements 0 parmi
d'événements 0 parmi 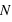 lancers, il est possible d'effectuer
lancers, il est possible d'effectuer 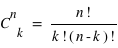 permutations. Donc la probabilité recherchée, notée
permutations. Donc la probabilité recherchée, notée 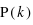 , vaut
, vaut 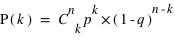 .
.
Sur 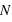 lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en
lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en ![E[(N+1)*p]](../pages_stat-theorie/equations_stat-theorie/equation118.png) , où
, où 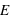 est la partie entière. Si p tend vers 1 alors le pic tendra vers
est la partie entière. Si p tend vers 1 alors le pic tendra vers 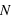 , à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut
, à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut 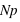 et son écart type vaut
et son écart type vaut 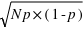 . Dans le cas ou
. Dans le cas ou 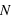 est très grand, un million par exemple, Le rapport écart-type sur espérance vaut
est très grand, un million par exemple, Le rapport écart-type sur espérance vaut 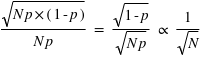 , il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si
, il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si 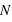 est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité,
est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité, 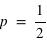 . Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur
. Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur 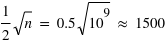 ; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les
; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les 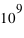 atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.