Probabilités
Auteur: Sylvain Fouquet
- Probabilités
- Les variables aléatoires
- La fonction de probabilité
- Probabilité sur des sous-ensembles d'événements
- Calcul de la fonction de probabilité
- Introduction aux théorème de Bayes - Découvrir la bonne urne
- Théorème de Bayes
- Grandeurs classiques en probabilité
- Fonctions de distribution
- Loi binomiale
- La loi de Poisson
- La loi normale
Probabilités
Statistique et probabilité sont deux côtés d'une même pièce. Ces deux domaines des mathématiques s'occupent de décrire le résultat d'expériences ou d'observations faisant intervenir le hasard. Par exemple, tirer un bulletin dans une urne, choisir des personnes au hasard dans un groupe, sélectionner des étoiles au hasard dans le ciel, etc, ne peuvent pas se décrire par la mécanique classique, l'hydrodynamique ou encore le magnétisme mais par la statistique et les probabilités. Pourquoi avoir deux noms ? Statistique et probabilité ne sont pas identiques dans la démarche bien que traitant des mêmes sujets. La statistique sert à observer et décrire le monde alors que les probabilités, aussi appelés théorie de la probabilité, tentent de l'expliquer théoriquement, mathématiquement. Ces deux approches se complètent mutuellement comme l'observation physique et le modèle mathématique se complètent.
L'expérience de 100 lancers du même dé servira à illustrer la différence entre statistique et probabilité. Lors de cette expérience, la statistique décrit les propriétés statistiques de ces 100 lancers. Par exemple, la statistique montre que chaque face du dé est presque apparue autant de fois. La valeur moyenne se rapproche de 3,5. De manière complémentaire à cet aspect observationnel, la théorie de la probabilité prouve que si vous avez un dé non pipé, il y a autant de chance de tomber sur une face que sur une autre. Pour un nombre de 100 lancers, la théorie de la probabilité indique quelle est la chance d'obtenir la face 1 par exemple. Les prévisions de la théorie de la probabilité doivent se confirmer dans les résultats observationels de la statistique. Si tel n'est pas le cas pour les lancers de dé, cela veut dire que le dé est pipé et qu'il faut changer les lois de probabilité (passer de la loi "chaque valeur a une chance sur 6 de sortir" à une loi plus compliquée qui va définir le dé pipé), à l'instar d'une expérience mettant en échec une théorie physique.
Les variables aléatoires
L'univers des événements
En probabilité, les variables sont dites aléatoires car pour, une même expérience, la mesure de la même observable sera différente, aléatoire. Par exemple lorsqu'un dé est lancé, l'observable qui est le numéro du dé est aléatoire (à moins qu'il ne soit envoyé par une machine pouvant envoyer le dé à chaque fois exactement de la même façon). Ce qui importe pour une variable aléatoire c'est l'ensemble des valeurs qu'elle peut prendre. Pour un dé, il y a six faces ; le nombre d'événements possibles est six (on suppose que le dé ne peut pas s'arrêter sur une arête). Autre exemple, la variable donnant l'instant du prochain accident de voiture en France peut prendre n'importe quelle valeur à priori entre 0 seconde et l'infini : 1 secondes, 10 minutes, 1 heures, etc. Il y a une infinité de possibilités.
Il existe donc deux types de variables aléatoires : les variables discrètes (lancer de dés) et les variables continues (temps entre deux accidents). Pour les variables discrètes, le nombre d'evénements peut être fini ou infini. Il est toujours infini pour une variable continue. L'ensemble des évènements est appelé l'ensemble univers des évènements. La suite donne quelques exemples détaillés de ces types d'ensembles. En probabilité, les événements sont très souvent associés à des nombres pour pouvoir être traités mathématiquement. Par exemple pour un jeu de cartes, la carte roi de pique peut être associée à la valeur numérique de 25.
Exemples de variables discrètes
L'ensemble univers le plus connu et le plus simple de tous est l'ensemble des évènements d'un jet d'une pièce de monnaie. Il n'y a que deux évènements : {pile ; face} (trois évènements si l'on prend en compte le cas où la pièce reste sur son bord). Par commodité, on utilise l'ensemble {0, 1} en liant pile à 0 et face à 1.
L'autre variable aléatoire très connue est le lancer de dé avec ses six évènements possibles qui sont déjà des nombres : {1, 2, 3, 4, 5, 6}. Il est aussi possible de lancer deux dés à la fois et de sommer leurs résultats. Dans ce cas, cela conduit à un ensemble de 11 évènements {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Des urnes remplies de boules de différentes couleurs sont aussi un exemple très pédagogiques d'ensemble univers. Par exemple, pour une urne remplie de 5 boules qui ne se différencient que par leurs couleurs : 2 noires, 2 blanches et 1 rouge, l'ensemble des évènements si l'on tire une boule est {noire, blanche, rouge}. Si l'on en tire deux, c'est alors {(noire, noire), (noire, blanche), (noire, rouge), (blanche, rouge)}. Encore une fois, il faut associer chaque couleur à un nombre pour pouvoir travailler dessus.
Enfin, pour les joueurs d'argent, et les aficionados de probabilités à variables discrètes, le casino est l'endroit rêvé. Il est possible de trouver là une multitude de jeux avec des ensembles univers allant de la case rouge ou noir à des images sur une machine à sous. Les casinos utilisent bien évidemment aussi les jeux de cartes pour enrichir le nombre d'évènement possibles.
Bref, les variables aléatoires discrètes sont partout dans la société. C'est d'ailleurs souvent à la suite de créations de la société : pièces, dés, cartes, roulette, loto, ...
Exemples de variables continues
Les variables continues se trouvent plus souvent liées à des propriétés physiques de la nature. Un exemple simple peut se trouver dans les prévisions météorologiques : "Quand pleuvra-t-il chez moi ?". La réponse se trouve être entre tout de suite (0 seconde) et jamais (un temps infini). Il y a donc une infinité continue de durées possibles. Il peut se passer plusieurs jours sans pleuvoir alors que parfois moins d'une heure s'écoule entre deux averses. Cet exemple de variable aléatoire est similaire à celui de l'intervalle de temps entre deux accidents de voitures. Plus généralement, il se trouve que certains phénomènes naturels n'arrivent pas de manière régulière. On peut alors introduire la variable aléatoire qui donne le temps entre deux occurences.
Un autre type de variables aléatoires continues sont les incertitudes dues à de faibles changements des conditions initiales. Refaire exactement la même chose un grand nombre de fois donne un résultat similaire mais pas identique. Lancer un poids est un de ces cas. Vous aurez beau faire attention, vous ne lancerez jamais avec exactement la même force, dans la même position et dans les mêmes conditions (vent, atterissage, etc). La conséquence est que le poids ne tombera jamais au même endroit. Il en est de même pour la production de pièces en série qui ne sont jamais tout à fait identiques. Tous ces cas peuvent se traiter avec les variables aléatoires continues.
La fonction de probabilité
En probabilité, après avoir défini l'ensemble univers des évènements, il reste à associer à chaque évènement sa probabilité de se produire via la fonction de probabilité. Cette fonction prend des valeurs entre 0 et 1. La valeur 0 signifie que l'évènement est impossible, la valeur 1 qu'il est certain.
Par exemple, dans le cas d'un jet d'une pièce non faussée, l'ensemble des évènements est {pile, face}, ou {0, 1}, et la fonction de probabilité, notée 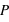 , donne
, donne 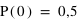 et
et 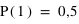 . Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant :
. Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant : 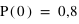 et
et 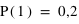 . "pile" aurait alors 4 fois plus de chance de sortir.
. "pile" aurait alors 4 fois plus de chance de sortir.
Cette loi nous amène à une propriété bien naturelle des probabilités.
La probabilité de l'ensemble univers vaut 1 : P(Univers) = 1.
En effet, il est certain que la variable aléatoire sorte un évènement de l'ensemble univers. Dans le cas d'un lancer de dé, P({1, 2, 3, 4, 5, 6}) = 1, car on est sûr d'obtenir comme résultat 1, 2, 3, 4, 5 ou 6. A l'inverse, l'ensemble vide {} a toujours une probabilité nulle : P({}) = 0.
Probabilité sur des sous-ensembles d'événements
Dans le cas, d'un dé non pipé, la fonction de probabilité est pour tous 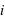 de 1 à 6,
de 1 à 6, 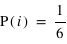 . Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc
. Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc 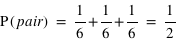 . Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
. Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
Voyons comment calculer la probabilité de l'union de deux sous-ensembles. Par exemple au jeu de 52 cartes, la probabilité de tirer n'importe quelle carte est la même et vaut 1/52. Dans ce cas, la probabilité de tirer une carte rouge vaudra 1/52 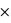 26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
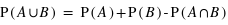
où A et B sont deux sous-ensembles de l'ensemble univers, 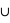 l'union de deux ensembles et
l'union de deux ensembles et 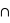 leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge
leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge 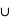 rois) = P(rouge) + P(rois) - P(rois
rois) = P(rouge) + P(rois) - P(rois 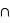 rouge). Il se trouve que l'ensemble {rois
rouge). Il se trouve que l'ensemble {rois 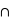 rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2
rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2 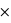 1/52 = 1/26. Le résultat est donc P(rois
1/52 = 1/26. Le résultat est donc P(rois 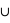 rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
Notons que si {A 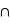 B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A
B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A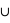 B car P({}) = 0.
B car P({}) = 0.
Calcul de la fonction de probabilité
Équipartition
Dans le cas d'un ensemble fini, il est parfois très facile de calculer la fonction de probabilité. Il suffit que tous les événements soient équiprobables, c'est à dire qu'ils aient la même probabilité, notée 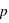 . Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p =
. Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p = 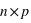 car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous
car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous 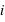 et
et 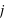 , {
, {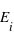
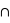
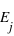 } = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc
} = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc 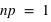 ce qui implique que
ce qui implique que 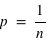 . Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.
. Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.

Loi des grands nombres
Lorsqu'il n'y a pas équipartition dans les probabilités, il est moins direct de déduire la loi de probabilité. Une façon simple en théorie mais hélas irréalisable en pratique est la loi des grands nombres. Pour connaître la loi de probabilité, il suffit de mesurer plusieurs fois la valeur d'une variable aléatoire, de compter combien de fois sortent les mêmes valeurs puis de diviser ces nombres par le nombre total d'essais. Ainsi pour connaître la loi d'un dé, il suffit de faire une grand nombre de lancers, 1000 par exemple, et de regarder combien de 1 de 2 de 3, ... et de 6 sont sortis et enfin de diviser ces nombres d'occurences par le nombre total de lancers, 1000 dans ce cas. Cela fournit une valeur proche de la probabilité de chaque évènement mais pas exacte. La théorie mathématique prouve que si le nombre total d'essais est infini (ce qui est évidemment impossible en pratique), on en déduit alors la probabilité exacte pour chaque événement.

Pour des variables continues où les résultats sont des réels, deux résultats ne peuvent jamais être identiques car la chance d'avoir exactement deux réels identiques est nulle. Ce qui est mesuré est la probabilité d'avoir des valeurs dans un petit intervalle autour d'une valeur donnée. De toute façon, les outils de mesure n'étant pas parfaits, il est impossible de mesurer avec une précision infinie. La largeur des intervalles considérés dépendra donc de la précision des mesures.
Introduction aux théorème de Bayes - Découvrir la bonne urne
Considérons deux urnes, l'une remplie de 9 boules blanches et d'une seule boule noire, appelée A, et l'autre remplie de 9 boules noires et d'une boule blanche, appelée B. Il est interdit de voir leur contenu, on ne peut qu''en extraire une boule. Le problème est de savoir quelle est l'urne A parmi les deux urnes ? Sans faire aucun tirage de boule, la probabilité qu'une urne donnée soit l'urne A est la même pour les deux urnes et vaut donc 0,5, une chance sur deux, car il n'y a que deux événements.
Le problème ici n'est pas de connaître la probabilité de tirer des boules blanches ou noires dans les urnes A ou B mais de savoir depuis quelle urne sont tirées les boules en s'aidant du résultat du tirage d'une urne. Ce sont alors des probabilités conditionnelles : sachant qu'un résultat est vrai, quelle est la probabilité qu'un autre le soit aussi ? Ce problème simple d'urne peut s'extrapoler dans le cas de théories physiques. Imaginons que deux théories (deux urnes) soient en concurrence pour expliquer les mêmes phénomènes statistiques (tirage de boules). En faisant quelques observations (en tirant quelques boules), il est alors possible de montrer qu'une théorie est plus probable qu'une autre. Il est aussi possible que les deux théories se trompent (en tirant une boule rouge d'une des deux urnes).
De plus, avec les probabilités conditionnelles, il est possible d'estimer des grandeurs physiques via la mesure d'autres grandeurs. Un exemple caricatural éclaircira ce principe. Ayant les yeux bandés, je cherche à savoir si j'ai devant moi un norvégien ou un espagnol. Je peux estimer la taille de la personne mais pas voir son passeport. Comme j'ai une pensée très caricaturale, pour moi tous les norvégiens sont grands blonds aux yeux bleux et tous les espagnols sont petits bruns aux yeux marrons. Donc si j'ai devant moi une personne plutôt grande, je dirai que c'est un norvégien. De plus, s'il m'est permis de ne regarder que ses cheveux et qu'ils sont blonds, ma certitude grandit. La taille et la couleur des cheveux que j'ai pu observer servent à estimer avec une certaine probabilité la nationalité d'une personne. Cette méthode repose sur une loi conditionnelle implicite qui est qu'un homme grand aux yeux bleus à une plus forte probabilité d'être norvégien qu'espagnol. Cette démarche est beaucoup utilisée en astrophysique pour déterminer des propriétés inaccessibles par des mesures directes, mais déductibles par d'autres propriétés observables. Cependant, il est important de se souvenir que ce ne sont que des probabilités. D'autre part, cela suppose que les lois conditionnelles supposées a priori soient correctes.
Théorème de Bayes
Venons-en aux formules qui permettent concrètement de résoudre le problème de l'urne. Soient A et B deux expériences. La probabilité de A sachant B vrai, noté P(A|B), est donnée par la loi suivante, dite formule de Bayes établie par le mathématicien et pasteur Thomas Bayes au XVIIIe siècle :
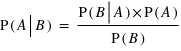
Il suffit de connaître P(A), P(B) et P(B|A) pour en déduire P(A|B).
Ce théorème provient du fait que 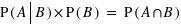 et que, de même,
et que, de même, 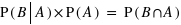 donc que
donc que 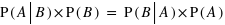 .
.
Dans le cas particulier des urnes, si l'on tire une boule blanche quelle est alors la probabilité que ce soit de l'urne A, probabilité notée P(Urne A|Blanche), ou de l'urne B, P(Urne B|Blanche) ? Dans le cas de l'urne A, il faut calculer les trois probabilités P(Blanche|Urne A), P(Urne A) et P(Blanche). La probabilité de tirer une boule blanche dans l'urne A est P(Blanche|Urne A) = 9/10. La probabilité de choisir l'urne A ou B est identique au début de l'expérience et vaut P(Urne A) = P(Urne B) = 0,5. Enfin la probabilité de tirer une boule blanche est P(Urne A)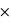 P(Blanche|Urne A)+P(Urne B)
P(Blanche|Urne A)+P(Urne B)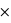 P(Blanche|Urne B) = 0,5
P(Blanche|Urne B) = 0,5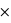 9/10 + 0,5
9/10 + 0,5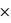 1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)
1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)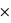 P(Urne A)/P(Blanche) = 9/10
P(Urne A)/P(Blanche) = 9/10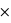 0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
Grandeurs classiques en probabilité
L'espérance
En théorie des probabilités, l'espérance est la valeur moyenne à laquelle on s'attend pour une variable aléatoire suivant une loi de probabilité donnée. Elle se définit dans le cas d'une variable discrète par la relation suivante : 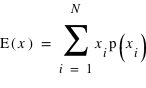 . De manière similaire, elle se définit pour une variable continue
. De manière similaire, elle se définit pour une variable continue  :
: 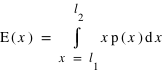 où
où 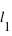 et
et 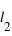 sont les limites inférieures et supérieures que peut prendre la variable
sont les limites inférieures et supérieures que peut prendre la variable 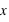 .
.
Un exemple dans la cas d'une variable discrète est la moyenne au lancer d'un dé. L'espérance est alors 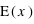 = 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (
= 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (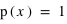 ), l'espérance est
), l'espérance est 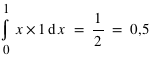 . Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
. Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
Le moment d'ordre deux centré - la variance
La variance ou "moment d'ordre deux centré" est une mesure du carré de la dispersion d'une variable aléatoire autour de son espérance. En d'autres termes, la variance donne une information sur la dispersion de la variable aléatoire autour de l'espérance. Plus la variance est grande plus les valeurs de la variable aléatoire auront de chance d'être loin de l'espérance, et vice versa. Une variance faible donnera une loi de probabilité piquée autour de l'espérance. Pour une variable discrète, la variance se définit comme suit : 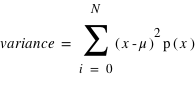 avec
avec 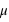 l'espérance. Dans le cas d'une variable continue,
l'espérance. Dans le cas d'une variable continue, 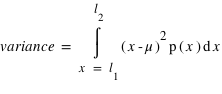 . On peut aussi définir la variance en n'utilisant que l'espérance de la variable
. On peut aussi définir la variance en n'utilisant que l'espérance de la variable 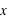 et
et 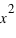 :
: 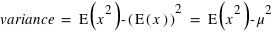 . La démonstration est demandée en exercice. L'écart-type, souvent noté
. La démonstration est demandée en exercice. L'écart-type, souvent noté 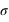 , est la racine carrée de la variance :
, est la racine carrée de la variance : 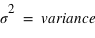 . De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
. De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
Pour le lancer de dé non biaisé, la variance vaut environ 2,91667 et donc l'écart type vaut environ 1,70783. Pour la loi uniforme de 0 à 1, la variance vaut 1/12 ≈ 0,0833.
Fonctions de distribution
Fonctions de distribution
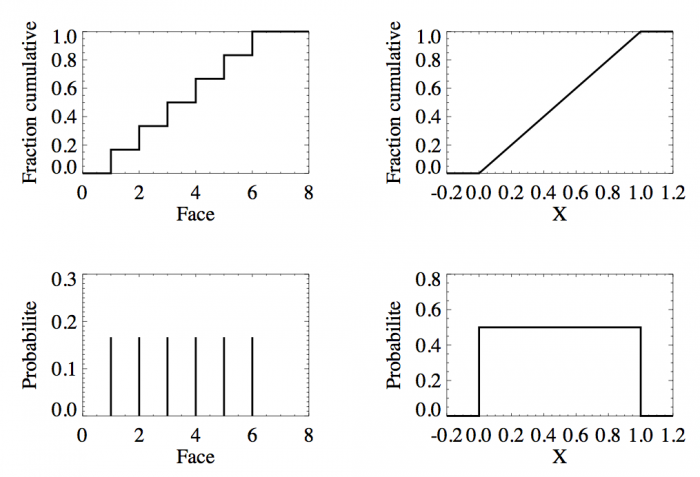
Fonctions de distribution (en haut) et lois de probabilité (en bas) du lancer d'un dé (à gauche) et de la loi uniforme sur [0, 1] (à droite).
Crédit :
Sylvain Fouquet
Avant de décrire plusieurs lois de probabilité utiles car très courantes, cette section décrit l'outil majeur qu'est la fonction de distribution et sa dérivée, la loi de probabilité.
Fonction de distribution
Pour une variable aléatoire notée 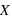 , la fonction de distribution, notée
, la fonction de distribution, notée 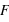 , donne la probabilité d'avoir la variable
, donne la probabilité d'avoir la variable 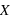 strictement plus petite que
strictement plus petite que 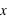 :
: 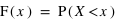 . La fonction
. La fonction 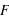 est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable
est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable 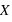 entre
entre 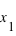 et
et 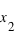 . C'est tout simplement
. C'est tout simplement 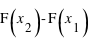 . En conséquence, si la courbe est plate ou avec une pente faible entre deux points
. En conséquence, si la courbe est plate ou avec une pente faible entre deux points 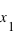 et
et 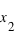 , cela conduit à une probabilité entre
, cela conduit à une probabilité entre 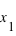 et
et 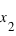 faible alors que si la pente est forte la probabilité l'est aussi.
faible alors que si la pente est forte la probabilité l'est aussi.
La figure en haut à gauche montre la fonction de distribution d'un dé. Pour 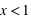 , la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De
, la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De 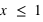 à
à 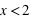 ,
,  est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut
est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut 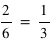 ; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
La figure en haut à droite montre la fonction de distribution d'une variable continue. En dessous de 0, sa valeur est nulle au dessus de 1 elle vaut 1. Les valeurs possibles de cette variable sont donc comprises entre 0 et 1 inclus. La pente est une droite ; pour n'importe quel intervalle entre 0 et 1 de même taille la probabilité est donc la même. En conséquence, la probabilité d'avoir une valeur entre [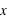 ,
, 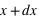 ] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
Loi de probabilité
La fonction de distribution est l'outil statistique par excellence en probabilité. Cependant, d'un point de vue pratique, on lui préfère sa dérivée qui est plus parlante : la loi de probabilité. En effet, c'est la pente de la fonction de distribution qui indique si une valeur a une forte probabilité ou pas de survenir. Cela revient en statistique à faire l'histogramme vu aussi dans la première partie de ce cours.
La figure en bas à gauche montre la dérivée de la fonction de distribution pour un lancer de dé. On retrouve le résultat classique qui veut que la probabilité de sortir un 1, 2, 3, 4, 5, ou 6 soit identique et égale à 1/6. La figure en bas à droite fait de même mais avec la loi uniforme entre 0 et 1. La fonction est une courbe plate montrant bien que chaque valeur a une même probabilité.
Par la suite et pour finir cette partie théorique, plusieurs lois de probabilité incontournables sont passées en revue. La liste est évidemment non exhaustive.
Loi binomiale
La loi binomiale
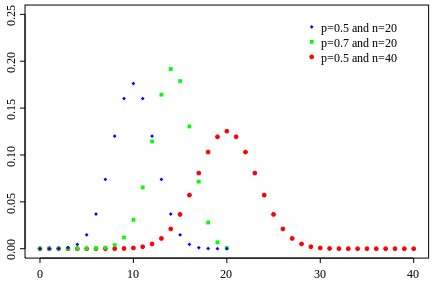
Exemples de lois binomiales pour différent nombre de répétition (
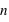
) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (
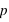
). Pour le même nombre de lancers
, le pic est à 14 avec un probabilté
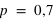
et seulement 10 avec
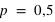
. Pour
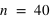
et
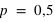
, le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de
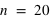
et
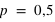
, lorsque
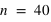
, la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque
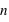
tend vers l'infini.
Crédit :
Wikipédia
Loi binomiale
En compléxifiant la loi vue ci-dessus, il est possible de créer la loi binomiale. Cette dernière s'intéresse aux résultats de plusieurs lancers d'une expérience n'ayant que deux événements possibles. Par exemple, lorsqu'une pièce est lancée 20 fois de suite, quelle est la probabilité d'avoir 10 faces ou 3 piles ou même 20 faces de suite ? La loi binomiale dépend donc de deux paramètres : la propabilité 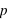 de la loi à deux événements et le nombre de répétition de cette loi,
de la loi à deux événements et le nombre de répétition de cette loi, 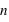 . Son ensemble univers est constitué de toutes les séries possibles de
. Son ensemble univers est constitué de toutes les séries possibles de 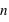 répétitions de la loi à deux évènements. Le nombre d'événements vaut donc
répétitions de la loi à deux évènements. Le nombre d'événements vaut donc 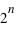 car à chaque répétition (
car à chaque répétition (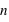 en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne
en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne 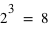 évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté
évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté 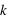 , et de 1, noté
, et de 1, noté 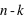 . Par définition la probabilité de 0 vaut
. Par définition la probabilité de 0 vaut 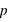 et celle de 1 vaut
et celle de 1 vaut 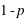 . Donc la probabilité d'un évènement est
. Donc la probabilité d'un évènement est 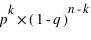 . L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer
. L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer 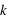 évènements 0 sur
évènements 0 sur 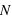 lancers. Pour cela, il suffit de remarquer que pour un nombre
lancers. Pour cela, il suffit de remarquer que pour un nombre 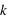 d'événements 0 parmi
d'événements 0 parmi 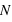 lancers, il est possible d'effectuer
lancers, il est possible d'effectuer 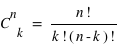 permutations. Donc la probabilité recherchée, notée
permutations. Donc la probabilité recherchée, notée 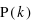 , vaut
, vaut 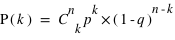 .
.
Propriétés de la loi binomiale
Sur 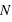 lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en
lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en ![E[(N+1)*p]](../pages_stat-theorie/equations_stat-theorie/equation118.png) , où
, où 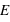 est la partie entière. Si p tend vers 1 alors le pic tendra vers
est la partie entière. Si p tend vers 1 alors le pic tendra vers 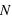 , à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut
, à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut 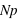 et son écart type vaut
et son écart type vaut 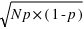 . Dans le cas ou
. Dans le cas ou 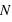 est très grand, un million par exemple, Le rapport écart-type sur espérance vaut
est très grand, un million par exemple, Le rapport écart-type sur espérance vaut 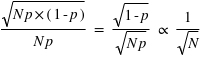 , il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si
, il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si 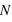 est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité,
est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité, 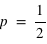 . Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur
. Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur 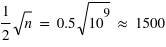 ; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les
; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les 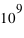 atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
La loi de Poisson
Loi de Poisson
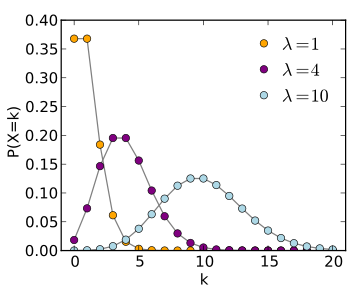
Trois exemples de loi de probabilité derivé de la loi de Poisson pour trois valeurs de
: 1, 4 et 10.
Crédit :
Wikipédia
Définition
La loi de Poisson, nommée d'après le mathématicien français Siméon Denis Poisson, s'applique à une variable discrète mais pouvant prendre des valeurs arbitrairement grandes. Son ensemble univers peut alors se confondre avec l'ensemble des entiers naturels. La loi de Poisson dépend d'un paramètre noté par usage 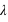 . La loi de probabilité de la loi de Poisson est
. La loi de probabilité de la loi de Poisson est 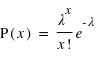 toujours positive (voir figure). Si
toujours positive (voir figure). Si 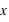 vaut 0, comme
vaut 0, comme 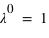 et
et 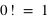 , alors
, alors 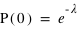 . Lorsque
. Lorsque 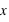 tend vers l'infini,
tend vers l'infini, 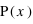 tend vers 0 du fait du terme en factorielle qui domine le terme
tend vers 0 du fait du terme en factorielle qui domine le terme 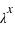 . Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de
. Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de 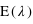 , si
, si 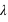 n'est pas un entier, et deux pics,
n'est pas un entier, et deux pics, 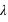 et
et 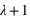 , si
, si 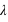 est un entier. L'espérance ainsi que la variance de cette fonction valent
est un entier. L'espérance ainsi que la variance de cette fonction valent 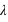 . L'écart type vaut donc
. L'écart type vaut donc 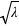 .
.
Bruit de photons
Il a déjà été fait mention dans la première partie de ce cours sur les statistiques des exoplanètes, que les photons captés pendant un temps 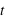 par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
La loi normale
Loi normale
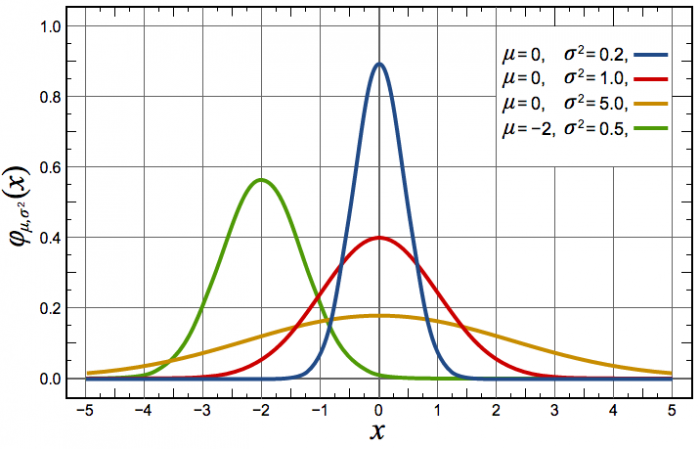
Trois exemples de fonctions de probabilités de loi normale avec différents espérances et écart-types.
Crédit :
Wikipédia
Fonction de distribution de la loi normale
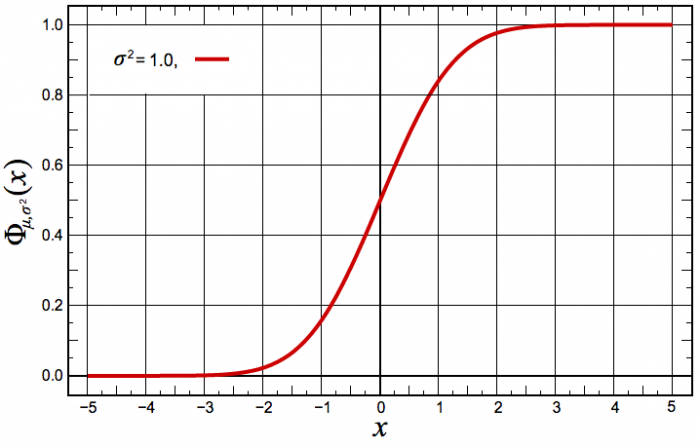
La fonction de distribution de la loi normale dont l'écart-type vaut 1 et l'espérance 0.
Crédit :
Wikipédia
Ecart-type de la loi normale
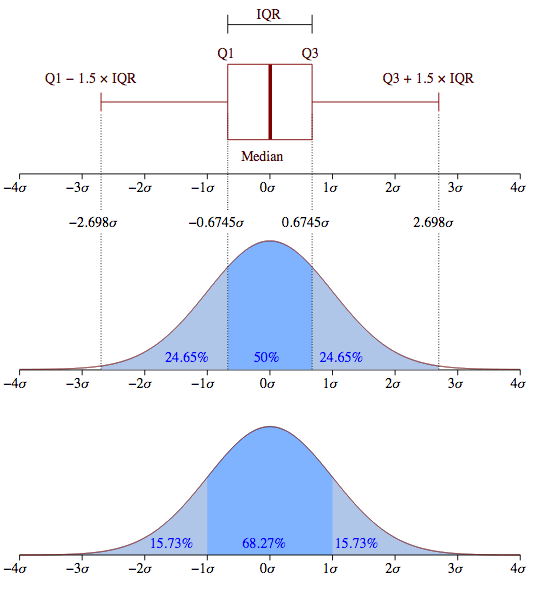
Figure du haut, boîte à moustaches représentant l'espace interquartile, les extrema théoriques étant à l'infini. Figure du milieu, la valeur exprimée en
des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [
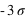
,
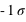
] (15,73 %), entre [
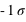
,
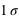
] (68,27 %) et enfin entre [
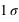
,
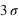
] (15,73 %).
Crédit :
Wikipédia
Définition
La dernière loi décrite est la plus connue si ce n'est la plus utilisée dans le domaine des statistiques. C'est le prolifique mathématicien allemand Carl Frierich Gauss qui la popularisa, elle porte son nom : la loi gaussienne aussi appelée loi normale. A l'inverse des deux précedentes lois, elle s'applique sur l'ensemble des réels. Pour un intervalle [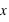 ,
, 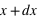 ], cette loi de probabilité vaut :
], cette loi de probabilité vaut : 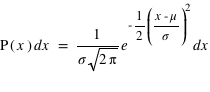 . Elle a deux paramètres qui sont
. Elle a deux paramètres qui sont 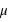 , l'espérance de la fonction de probabilité, et
, l'espérance de la fonction de probabilité, et 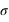 , l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis
, l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis 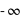 jusque
jusque 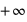 , vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne,
, vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne, 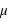 . L'écart-type à l'espérance est donné par
. L'écart-type à l'espérance est donné par 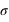 . A
. A 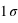 la probabilité chute d'une facteur
la probabilité chute d'une facteur 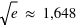 ; à
; à 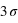 , ce facteur devient
, ce facteur devient 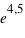 , soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de
, soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de 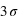 de la moyenne devient très faible, et cette probabilité devient quasiment nulle à
de la moyenne devient très faible, et cette probabilité devient quasiment nulle à 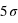 (voir la troisième figure).
(voir la troisième figure).
Une loi pour les erreurs de mesures
Lorsqu'une expérience est effectuée plusieurs fois, un résultat un peu différent de celui attendu apparaît. La différence entre la vraie valeur et notre mesure est appelée l'erreur. Par exemple, dans le cas de la fabrication de pièces mécaniques dans l'industrie, aucune pièce n'est strictement identique à une autre. Il y a donc un écart (une erreur) à la valeur désirée par le fabricant. Les causes des erreurs peuvent être multiples mais si elles sont sans lien entre elles (on dit qu'elles sont indépendantes), alors la loi de probabilité suivie par les erreurs est une gaussienne. Deux qualificatifs caractérisent une expérience ou la machine fabriquant une pièce mécanique : la fiabilité et la précision. La fiabilité informe si vous êtes en accord avec l'espérance en calculant la différence entre la moyenne obtenue et la valeur réelle. La précision quantifie l'incertitude pour chaque expérience, elle est donnée par l'écart-type, 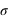 . Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
. Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
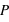 , donne
, donne 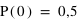 et
et 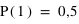 . Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant :
. Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant : 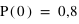 et
et 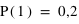 . "pile" aurait alors 4 fois plus de chance de sortir.
. "pile" aurait alors 4 fois plus de chance de sortir.
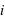 de 1 à 6,
de 1 à 6, 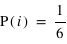 . Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc
. Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc 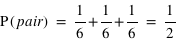 . Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
. Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
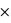 26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
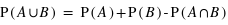
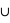 l'union de deux ensembles et
l'union de deux ensembles et 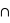 leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge
leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge 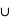 rois) = P(rouge) + P(rois) - P(rois
rois) = P(rouge) + P(rois) - P(rois 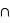 rouge). Il se trouve que l'ensemble {rois
rouge). Il se trouve que l'ensemble {rois 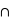 rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2
rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2 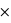 1/52 = 1/26. Le résultat est donc P(rois
1/52 = 1/26. Le résultat est donc P(rois 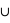 rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
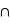 B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A
B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A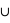 B car P({}) = 0.
B car P({}) = 0.
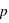 . Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p =
. Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p = 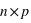 car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous
car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous 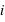 et
et 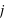 , {
, {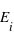
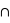
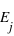 } = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc
} = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc 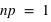 ce qui implique que
ce qui implique que 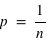 . Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.
. Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.

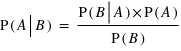
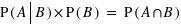 et que, de même,
et que, de même, 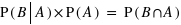 donc que
donc que 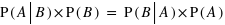 .
.
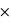 P(Blanche|Urne A)+P(Urne B)
P(Blanche|Urne A)+P(Urne B)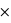 P(Blanche|Urne B) = 0,5
P(Blanche|Urne B) = 0,5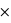 9/10 + 0,5
9/10 + 0,5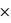 1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)
1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)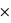 P(Urne A)/P(Blanche) = 9/10
P(Urne A)/P(Blanche) = 9/10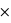 0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
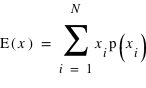 . De manière similaire, elle se définit pour une variable continue
. De manière similaire, elle se définit pour une variable continue 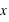 :
: 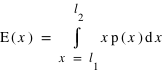 où
où 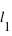 et
et 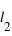 sont les limites inférieures et supérieures que peut prendre la variable
sont les limites inférieures et supérieures que peut prendre la variable 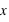 .
.
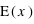 = 1
= 1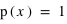 ), l'espérance est
), l'espérance est 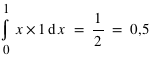 . Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
. Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
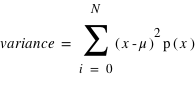 avec
avec 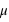 l'espérance. Dans le cas d'une variable continue,
l'espérance. Dans le cas d'une variable continue, 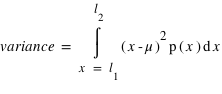 . On peut aussi définir la variance en n'utilisant que l'espérance de la variable
. On peut aussi définir la variance en n'utilisant que l'espérance de la variable 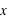 et
et 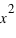 :
: 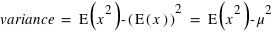 . La démonstration est demandée en exercice. L'écart-type, souvent noté
. La démonstration est demandée en exercice. L'écart-type, souvent noté 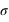 , est la racine carrée de la variance :
, est la racine carrée de la variance : 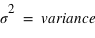 . De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
. De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.

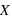 , la fonction de distribution, notée
, la fonction de distribution, notée 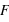 , donne la probabilité d'avoir la variable
, donne la probabilité d'avoir la variable 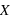 strictement plus petite que
strictement plus petite que 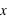 :
: 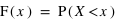 . La fonction
. La fonction 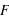 est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable
est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable 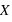 entre
entre 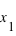 et
et 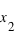 . C'est tout simplement
. C'est tout simplement 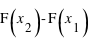 . En conséquence, si la courbe est plate ou avec une pente faible entre deux points
. En conséquence, si la courbe est plate ou avec une pente faible entre deux points 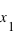 et
et 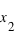 , cela conduit à une probabilité entre
, cela conduit à une probabilité entre 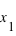 et
et 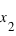 faible alors que si la pente est forte la probabilité l'est aussi.
faible alors que si la pente est forte la probabilité l'est aussi.
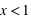 , la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De
, la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De 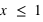 à
à 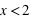 ,
,  est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut
est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut 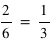 ; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
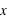 ,
, 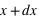 ] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.

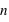 ) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (
) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (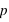 ). Pour le même nombre de lancers
). Pour le même nombre de lancers 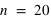 , le pic est à 14 avec un probabilté
, le pic est à 14 avec un probabilté 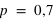 et seulement 10 avec
et seulement 10 avec 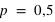 . Pour
. Pour 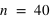 et
et 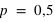 , le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de
, le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de 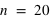 et
et 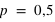 , lorsque
, lorsque 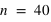 , la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque
, la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque 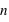 tend vers l'infini.
tend vers l'infini.
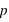 alors que l'événement 1 a une probabilité notée
alors que l'événement 1 a une probabilité notée 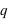 . Toujours, dans le cas d'une pièce de monnaie,
. Toujours, dans le cas d'une pièce de monnaie, 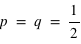 . De manière générale,
. De manière générale, 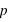 et
et 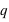 n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas
n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas 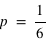 et
et 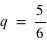 . De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité
. De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité 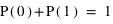 donc
donc 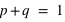 et
et 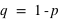 . Les lois à deux événements ne dépendent donc que d'un paramètre,
. Les lois à deux événements ne dépendent donc que d'un paramètre, 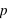 .
.
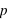 de la loi à deux événements et le nombre de répétition de cette loi,
de la loi à deux événements et le nombre de répétition de cette loi, 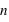 . Son ensemble univers est constitué de toutes les séries possibles de
. Son ensemble univers est constitué de toutes les séries possibles de 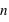 répétitions de la loi à deux évènements. Le nombre d'événements vaut donc
répétitions de la loi à deux évènements. Le nombre d'événements vaut donc 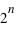 car à chaque répétition (
car à chaque répétition (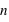 en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne
en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne 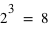 évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté
évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté 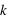 , et de 1, noté
, et de 1, noté 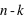 . Par définition la probabilité de 0 vaut
. Par définition la probabilité de 0 vaut 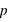 et celle de 1 vaut
et celle de 1 vaut 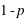 . Donc la probabilité d'un évènement est
. Donc la probabilité d'un évènement est 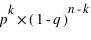 . L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer
. L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer 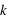 évènements 0 sur
évènements 0 sur 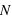 lancers. Pour cela, il suffit de remarquer que pour un nombre
lancers. Pour cela, il suffit de remarquer que pour un nombre 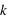 d'événements 0 parmi
d'événements 0 parmi 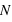 lancers, il est possible d'effectuer
lancers, il est possible d'effectuer 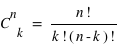 permutations. Donc la probabilité recherchée, notée
permutations. Donc la probabilité recherchée, notée 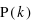 , vaut
, vaut 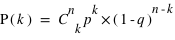 .
.
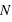 lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en
lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en ![E[(N+1)*p]](../pages_stat-theorie/equations_stat-theorie/equation118.png) , où
, où 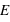 est la partie entière. Si p tend vers 1 alors le pic tendra vers
est la partie entière. Si p tend vers 1 alors le pic tendra vers 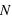 , à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut
, à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut 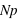 et son écart type vaut
et son écart type vaut 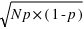 . Dans le cas ou
. Dans le cas ou 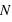 est très grand, un million par exemple, Le rapport écart-type sur espérance vaut
est très grand, un million par exemple, Le rapport écart-type sur espérance vaut 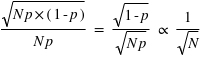 , il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si
, il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si 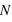 est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité,
est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité, 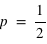 . Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur
. Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur 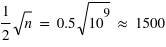 ; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les
; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les 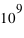 atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.

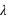 : 1, 4 et 10.
: 1, 4 et 10.
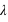 . La loi de probabilité de la loi de Poisson est
. La loi de probabilité de la loi de Poisson est 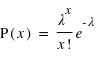 toujours positive (voir figure). Si
toujours positive (voir figure). Si 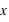 vaut 0, comme
vaut 0, comme 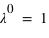 et
et 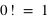 , alors
, alors 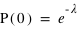 . Lorsque
. Lorsque 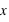 tend vers l'infini,
tend vers l'infini, 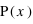 tend vers 0 du fait du terme en factorielle qui domine le terme
tend vers 0 du fait du terme en factorielle qui domine le terme 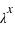 . Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de
. Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de 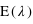 , si
, si 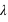 n'est pas un entier, et deux pics,
n'est pas un entier, et deux pics, 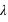 et
et 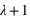 , si
, si 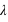 est un entier. L'espérance ainsi que la variance de cette fonction valent
est un entier. L'espérance ainsi que la variance de cette fonction valent 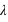 . L'écart type vaut donc
. L'écart type vaut donc 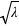 .
.
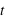 par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.



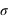 des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [
des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [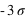 ,
, 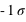 ] (15,73 %), entre [
] (15,73 %), entre [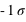 ,
, 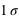 ] (68,27 %) et enfin entre [
] (68,27 %) et enfin entre [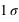 ,
, 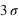 ] (15,73 %).
] (15,73 %).
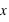 ,
, 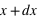 ], cette loi de probabilité vaut :
], cette loi de probabilité vaut : 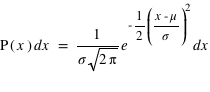 . Elle a deux paramètres qui sont
. Elle a deux paramètres qui sont 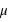 , l'espérance de la fonction de probabilité, et
, l'espérance de la fonction de probabilité, et 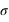 , l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis
, l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis 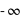 jusque
jusque 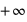 , vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne,
, vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne, 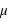 . L'écart-type à l'espérance est donné par
. L'écart-type à l'espérance est donné par 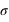 . A
. A 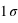 la probabilité chute d'une facteur
la probabilité chute d'une facteur 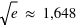 ; à
; à 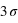 , ce facteur devient
, ce facteur devient 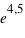 , soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de
, soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de 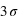 de la moyenne devient très faible, et cette probabilité devient quasiment nulle à
de la moyenne devient très faible, et cette probabilité devient quasiment nulle à 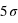 (voir la troisième figure).
(voir la troisième figure).
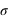 . Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
. Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.