Définition
La dernière loi décrite est la plus connue si ce n'est la plus utilisée dans le domaine des statistiques. C'est le prolifique mathématicien allemand Carl Frierich Gauss qui la popularisa, elle porte son nom : la loi gaussienne aussi appelée loi normale. A l'inverse des deux précedentes lois, elle s'applique sur l'ensemble des réels. Pour un intervalle [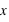
, 
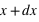], cette loi de probabilité vaut : 
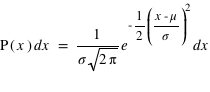. Elle a deux paramètres qui sont 
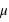, l'espérance de la fonction de probabilité, et 
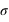, l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis 
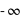jusque 
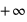, vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne, 
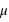. L'écart-type à l'espérance est donné par 
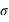. A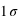 
la probabilité chute d'une facteur 
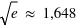; à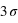 
, ce facteur devient 
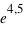, soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de 
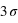de la moyenne devient très faible, et cette probabilité devient quasiment nulle à 
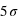(voir la troisième figure).
Une loi pour les erreurs de mesures
Lorsqu'une expérience est effectuée plusieurs fois, un résultat un peu différent de celui attendu apparaît. La différence entre la vraie valeur et notre mesure est appelée l'erreur. Par exemple, dans le cas de la fabrication de pièces mécaniques dans l'industrie, aucune pièce n'est strictement identique à une autre. Il y a donc un écart (une erreur) à la valeur désirée par le fabricant. Les causes des erreurs peuvent être multiples mais si elles sont sans lien entre elles (on dit qu'elles sont indépendantes), alors la loi de probabilité suivie par les erreurs est une gaussienne. Deux qualificatifs caractérisent une expérience ou la machine fabriquant une pièce mécanique : la fiabilité et la précision. La fiabilité informe si vous êtes en accord avec l'espérance en calculant la différence entre la moyenne obtenue et la valeur réelle. La précision quantifie l'incertitude pour chaque expérience, elle est donnée par l'écart-type,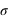 
. Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [
, 
] (15,73 %), entre [
, 
] (68,27 %) et enfin entre [
, 
] (15,73 %).