Fonctions de distribution

Fonction de distribution

Pour une variable aléatoire notée 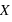, la fonction de distribution, notée 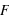, donne la probabilité d'avoir la variable 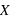strictement plus petite que 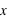: 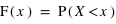. La fonction 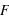est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. 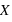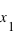Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable entre et 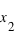. C'est tout simplement 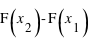. En conséquence, si la courbe est plate ou avec une pente faible entre deux points 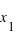et , cela conduit à une probabilité entre 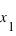et 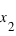faible alors que si la pente est forte la probabilité l'est aussi.

La figure en haut à gauche montre la fonction de distribution d'un dé. Pour 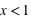, la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De 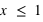à 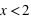, 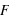est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut 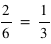; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.

La figure en haut à droite montre la fonction de distribution d'une variable continue. En dessous de 0, sa valeur est nulle au dessus de 1 elle vaut 1. Les valeurs possibles de cette variable sont donc comprises entre 0 et 1 inclus. La pente est une droite ; pour n'importe quel intervalle entre 0 et 1 de même taille la probabilité est donc la même. En conséquence, la probabilité d'avoir une valeur entre [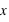, 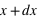] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.

Loi de probabilité

La fonction de distribution est l'outil statistique par excellence en probabilité. Cependant, d'un point de vue pratique, on lui préfère sa dérivée qui est plus parlante : la loi de probabilité. En effet, c'est la pente de la fonction de distribution qui indique si une valeur a une forte probabilité ou pas de survenir. Cela revient en statistique à faire l'histogramme vu aussi dans la première partie de ce cours.

La figure en bas à gauche montre la dérivée de la fonction de distribution pour un lancer de dé. On retrouve le résultat classique qui veut que la probabilité de sortir un 1, 2, 3, 4, 5, ou 6 soit identique et égale à 1/6. La figure en bas à droite fait de même mais avec la loi uniforme entre 0 et 1. La fonction est une courbe plate montrant bien que chaque valeur a une même probabilité.