La loi de Poisson

Auteur: Sylvain Fouquet

Loi de Poisson

Trois exemples de loi de probabilité derivé de la loi de Poisson pour trois valeurs de lambda

: 1, 4 et 10.

Crédit : Wikipédia

Définition

La loi de Poisson, nommée d'après le mathématicien français Siméon Denis Poisson, s'applique à une variable discrète mais pouvant prendre des valeurs arbitrairement grandes. Son ensemble univers peut alors se confondre avec l'ensemble des entiers naturels. La loi de Poisson dépend d'un paramètre noté par usage 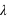lambda . La loi de probabilité de la loi de Poisson est 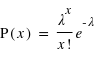P(x) = (lambda^x/fact(x))*e^(-lambda) toujours positive (voir figure). 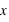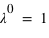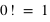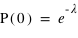Si vaut 0, comme lambda^0=1 et factorielle(0) = 1 , alors P(0) = e^(-lambda) . Lorsque 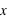tend vers l'infini, 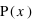P(x) tend vers 0 du fait du terme en factorielle qui domine le terme 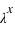. 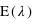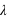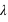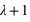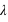Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de E(lambda) , si lambda n'est pas un entier, et deux pics, lambda et lambda+1 , si lambda est un entier. L'espérance ainsi que la variance de cette fonction valent 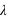lambda . 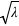L'écart type vaut donc sqrt(lambda) .

Bruit de photons

Il a déjà été fait mention dans la première partie de ce cours sur les statistiques des exoplanètes, que les photons captés pendant un temps 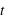par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.