| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Grandeurs classiques en probabilité |
En théorie des probabilités, l'espérance est la valeur moyenne à laquelle on s'attend pour une variable aléatoire suivant une loi de probabilité donnée. Elle se définit dans le cas d'une variable discrète par la relation suivante : 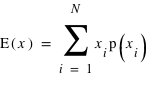 . De manière similaire, elle se définit pour une variable continue
. De manière similaire, elle se définit pour une variable continue 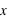 :
: 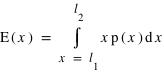 où
où 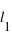 et
et 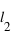 sont les limites inférieures et supérieures que peut prendre la variable
sont les limites inférieures et supérieures que peut prendre la variable 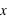 .
.
Un exemple dans la cas d'une variable discrète est la moyenne au lancer d'un dé. L'espérance est alors 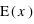 = 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (
= 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (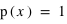 ), l'espérance est
), l'espérance est 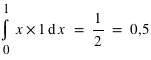 . Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
. Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
La variance ou "moment d'ordre deux centré" est une mesure du carré de la dispersion d'une variable aléatoire autour de son espérance. En d'autres termes, la variance donne une information sur la dispersion de la variable aléatoire autour de l'espérance. Plus la variance est grande plus les valeurs de la variable aléatoire auront de chance d'être loin de l'espérance, et vice versa. Une variance faible donnera une loi de probabilité piquée autour de l'espérance. Pour une variable discrète, la variance se définit comme suit : 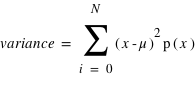 avec
avec 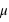 l'espérance. Dans le cas d'une variable continue,
l'espérance. Dans le cas d'une variable continue, 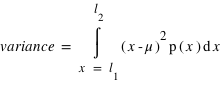 . On peut aussi définir la variance en n'utilisant que l'espérance de la variable
. On peut aussi définir la variance en n'utilisant que l'espérance de la variable 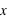 et
et 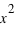 :
: 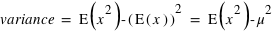 . La démonstration est demandée en exercice. L'écart-type, souvent noté
. La démonstration est demandée en exercice. L'écart-type, souvent noté 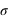 , est la racine carrée de la variance :
, est la racine carrée de la variance : 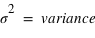 . De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
. De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
Pour le lancer de dé non biaisé, la variance vaut environ 2,91667 et donc l'écart type vaut environ 1,70783. Pour la loi uniforme de 0 à 1, la variance vaut 1/12 ≈ 0,0833.