Probabilité sur des sous-ensembles d'événements

Dans le cas, d'un dé non pipé, la fonction de probabilité est pour tous 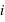de 1 à 6, 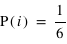. Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc 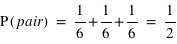. Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.

Voyons comment calculer la probabilité de l'union de deux sous-ensembles. Par exemple au jeu de 52 cartes, la probabilité de tirer n'importe quelle carte est la même et vaut 1/52. Dans ce cas, la probabilité de tirer une carte rouge vaudra 1/52 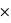26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est

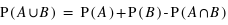
où A et B sont deux sous-ensembles de l'ensemble univers, 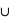l'union de deux ensembles et 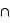leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge 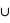rois) = P(rouge) + P(rois) - P(rois 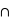rouge). Il se trouve que l'ensemble {rois 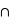rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2 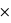1/52 = 1/26. Le résultat est donc P(rois 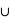rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.

Notons que si {A 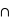B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A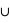B car P({}) = 0.