Calcul de la fonction de probabilité

Équipartition

Dans le cas d'un ensemble fini, il est parfois très facile de calculer la fonction de probabilité. Il suffit que tous les événements soient équiprobables, c'est à dire qu'ils aient la même probabilité, notée 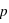. Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E₁, E₂, E₃, ..., E_n}) = P({E₁}) + P({E₂})+ P({E₃})+ ... + P({E_n}) = p +p +p +...+p = 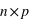car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous 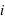et 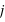, { 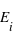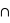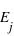} = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc 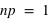ce qui implique que 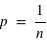. Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.

Loi des grands nombres

Lorsqu'il n'y a pas équipartition dans les probabilités, il est moins direct de déduire la loi de probabilité. Une façon simple en théorie mais hélas irréalisable en pratique est la loi des grands nombres. Pour connaître la loi de probabilité, il suffit de mesurer plusieurs fois la valeur d'une variable aléatoire, de compter combien de fois sortent les mêmes valeurs puis de diviser ces nombres par le nombre total d'essais. Ainsi pour connaître la loi d'un dé, il suffit de faire une grand nombre de lancers, 1000 par exemple, et de regarder combien de 1 de 2 de 3, ... et de 6 sont sortis et enfin de diviser ces nombres d'occurences par le nombre total de lancers, 1000 dans ce cas. Cela fournit une valeur proche de la probabilité de chaque évènement mais pas exacte. La théorie mathématique prouve que si le nombre total d'essais est infini (ce qui est évidemment impossible en pratique), on en déduit alors la probabilité exacte pour chaque événement.

Pour des variables continues où les résultats sont des réels, deux résultats ne peuvent jamais être identiques car la chance d'avoir exactement deux réels identiques est nulle. Ce qui est mesuré est la probabilité d'avoir des valeurs dans un petit intervalle autour d'une valeur donnée. De toute façon, les outils de mesure n'étant pas parfaits, il est impossible de mesurer avec une précision infinie. La largeur des intervalles considérés dépendra donc de la précision des mesures.