Présentation du modèle

Dans cette section on répond à la question suivante: pour un système planétaire donné, quelles seront les observations ? Dans la section précédente on a introduit la fonction 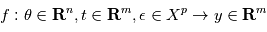$f: \theta \in \mathbf{R}^n,t \in \mathbf{R}^m , \epsilon \in X^p \rightarrow y \in \mathbf{R}^m$ , où 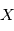désigne un espace de variables aléatoires, qui donne des observations 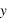en fonction d'instants d'observation 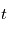, d'erreurs alétoires 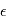$\epsilon$ et de paramètre du modèle 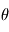$\theta$ incluant masse de la planète, de l'étoile, paramètres de l'orbites, etc. qui seront précisés. En l'occurrence, l'erreur est bien représentée par un "bruit additif", c'est à dire les observations 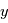sont de la forme 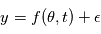$y=f(\theta,t) + \epsilon$ , où 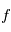désigne une fonction modélisant la physique du phénomène observée, celle qui donnerait les observations "parfaites", sans aucune source d'erreur aléatoire. L'erreur 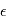$\epsilon$ modélise tous les phénomènes aléatoires intervenant dans les mesures. Selon la distinction adoptée ici, les paramètres du modèle peuvent inclure une source indésirable mais non aléatoire.

L'objet de ce chapitre est de construire cette fonction 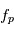f_p avec une modélisation physique. La modélisation la plus précise, utilisant tout ce que l'on sait de la physique serait ici inutilement complexe, car compte tenu des erreurs de mesures la différence avec certains modèles plus simples serait si faible qu'il serait impossible de la détecter avec un niveau de confiance acceptable. Le niveau de précision du modèle présenté ici est couramment utilisé par les observateurs.

Remarque: En pratique, les algorithmes d'estimation de paramètres sont des algorithmes d'optimisation, qui nécessitent tous de donner un ou plusieurs points de départs pour la recherche. Lorsque des modèles plus complexes sont utilisés, les estimations précises peuvent être utilisées comme tels.

On présentera d'abord une modélisation physique de l'objet étudié, puis d'autres effets physiques à prendre en compte. Les bruits instrumentaux seront traités dans le chapitre suivant. Les effets physiques "indépendants de l'observateur" qui seront pris en compte sont:

Le mouvement de l'étoile dû aux planètes.
Le mouvement propre: mouvement de translation du barycentre du système {Etoile+Planètes}
Des effets stellaires variables (Ondes de pression, granularité, activité)

Ensuite, on modélise "comment" la lumière émise par l'étoile nous parvient, ce qui amènera à présenter:

La prise en compte du mouvement de la Terre (vitesse de celle-ci dans le référentiel barycentrique du système solaire pour les vitesses radiales, parallaxe et réduction des observations en astrométrie.
Les perturbations atmosphériques
Les variations de parallaxe et de mouvement propre.