Modélisation - Problème direct
- Présentation du modèle
- Problème à deux corps
- Problème à deux corps newtonien
- Géométrie de l'orbite
- Loi des aires
- Exercices
- Equation de Kepler
- Solutions en fonction du temps
- Changement de référentiel
- Conclusion pour le problème à deux corps
- Exercices
- Modèle de la trajectoire
- Trajectoire observée depuis le barycentre du système solaire
- Trajectoire observée depuis la Terre
- Accélération de perspective et changement de parallaxe (astrométrie)
- Etoile
- Etoile
- Masse de l'étoile
- Processus stochastique et Densité spectrale de puissance
- Granulation
- Activité magnétique
- Oscillations radiales (vitesses radiales)
- Perturbations atmosphériques
- Récapitulation
Présentation du modèle
Dans cette section on répond à la question suivante: pour un système planétaire donné, quelles seront les observations ? Dans la section précédente on a introduit la fonction 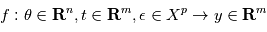 , où
, où 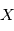 désigne un espace de variables aléatoires, qui donne des observations
désigne un espace de variables aléatoires, qui donne des observations 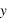 en fonction d'instants d'observation
en fonction d'instants d'observation 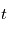 , d'erreurs alétoires
, d'erreurs alétoires 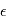 et de paramètre du modèle
et de paramètre du modèle 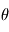 incluant masse de la planète, de l'étoile, paramètres de l'orbites, etc. qui seront précisés. En l'occurrence, l'erreur est bien représentée par un "bruit additif", c'est à dire les observations
incluant masse de la planète, de l'étoile, paramètres de l'orbites, etc. qui seront précisés. En l'occurrence, l'erreur est bien représentée par un "bruit additif", c'est à dire les observations 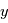 sont de la forme
sont de la forme 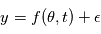 , où
, où 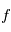 désigne une fonction modélisant la physique du phénomène observée, celle qui donnerait les observations "parfaites", sans aucune source d'erreur aléatoire. L'erreur
désigne une fonction modélisant la physique du phénomène observée, celle qui donnerait les observations "parfaites", sans aucune source d'erreur aléatoire. L'erreur 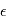 modélise tous les phénomènes aléatoires intervenant dans les mesures. Selon la distinction adoptée ici, les paramètres du modèle peuvent inclure une source indésirable mais non aléatoire.
modélise tous les phénomènes aléatoires intervenant dans les mesures. Selon la distinction adoptée ici, les paramètres du modèle peuvent inclure une source indésirable mais non aléatoire.
L'objet de ce chapitre est de construire cette fonction 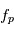 avec une modélisation physique. La modélisation la plus précise, utilisant tout ce que l'on sait de la physique serait ici inutilement complexe, car compte tenu des erreurs de mesures la différence avec certains modèles plus simples serait si faible qu'il serait impossible de la détecter avec un niveau de confiance acceptable. Le niveau de précision du modèle présenté ici est couramment utilisé par les observateurs.
avec une modélisation physique. La modélisation la plus précise, utilisant tout ce que l'on sait de la physique serait ici inutilement complexe, car compte tenu des erreurs de mesures la différence avec certains modèles plus simples serait si faible qu'il serait impossible de la détecter avec un niveau de confiance acceptable. Le niveau de précision du modèle présenté ici est couramment utilisé par les observateurs.
Remarque: En pratique, les algorithmes d'estimation de paramètres sont des algorithmes d'optimisation, qui nécessitent tous de donner un ou plusieurs points de départs pour la recherche. Lorsque des modèles plus complexes sont utilisés, les estimations précises peuvent être utilisées comme tels.
On présentera d'abord une modélisation physique de l'objet étudié, puis d'autres effets physiques à prendre en compte. Les bruits instrumentaux seront traités dans le chapitre suivant. Les effets physiques "indépendants de l'observateur" qui seront pris en compte sont:
- Le mouvement de l'étoile dû aux planètes.
- Le mouvement propre: mouvement de translation du barycentre du système {Etoile+Planètes}
- Des effets stellaires variables (Ondes de pression, granularité, activité)
Ensuite, on modélise "comment" la lumière émise par l'étoile nous parvient, ce qui amènera à présenter:
- La prise en compte du mouvement de la Terre (vitesse de celle-ci dans le référentiel barycentrique du système solaire pour les vitesses radiales, parallaxe et réduction des observations en astrométrie.
- Les perturbations atmosphériques
- Les variations de parallaxe et de mouvement propre.
Problème à deux corps
Auteur: Nathan Hara & Jacques Laskar
Problème à deux corps newtonien
Géométrie de l'orbite
Les quantités conservées définies page précédente permettent de donner une description géométrique de l'évolution de 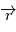 .
.
On déduit de la conservation du moment cinétique que le mouvement est plan. En effet, 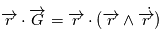 et comme
et comme 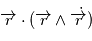 est un produit mixte, il est invariant par permutation circulaire:
est un produit mixte, il est invariant par permutation circulaire: 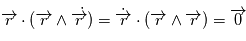 car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur
car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur 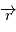 est orthogonal à
est orthogonal à 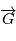 à tout instant, autrement dit le mouvement est dans un plan orthogonal à
à tout instant, autrement dit le mouvement est dans un plan orthogonal à 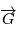 .
.
Notons 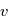 l'angle entre
l'angle entre 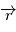 et
et 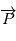 et posons
et posons 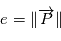 . Alors comme
. Alors comme 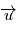 est unitaire,
est unitaire, 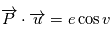 d'autre part en remplaçant
d'autre part en remplaçant 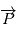 par sa définition, on a
par sa définition, on a 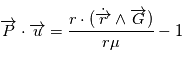 et comme
et comme 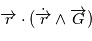 est un produit mixte,
est un produit mixte, 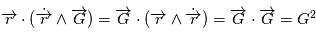 . où
. où 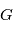 est la norme de
est la norme de 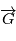 . On obtient alors
. On obtient alors 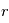 en fonction de
en fonction de 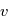 :
:
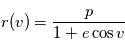
Où 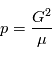 , qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de
, qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de 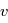 , appelée anomalie vraie. Cependant, nous voulons exprimer la solution en fonction du temps, l'objet de la page suivante est d'exhiber une relation entre
, appelée anomalie vraie. Cependant, nous voulons exprimer la solution en fonction du temps, l'objet de la page suivante est d'exhiber une relation entre 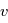 et le temps.
On sait que lorsque
et le temps.
On sait que lorsque 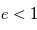 , il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que
, il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que 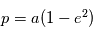 où
où 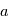 est le demi-grand axe de l'ellipse. Si
est le demi-grand axe de l'ellipse. Si 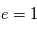 ou
ou 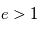 , la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
, la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
L'orbite est dans un plan perpendiculaire à 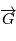 , et le vecteur
, et le vecteur 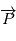 est parallèle à
est parallèle à 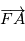 . Notons
. Notons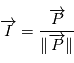 et
et 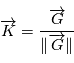 . On introduit un vecteur
. On introduit un vecteur 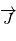 de sorte que
de sorte que 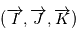 forme une base orthonormale.
forme une base orthonormale.
Géométrie du mouvement elliptique
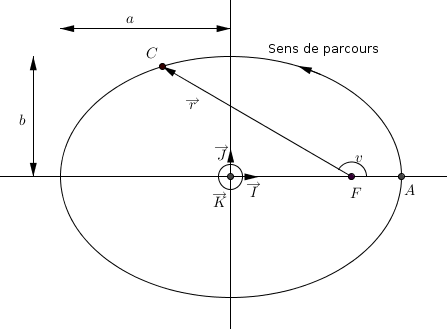
Le mouvement est dans le plan
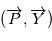
Loi des aires
Exercices
 Conservation de l'énergie
Conservation de l'énergie
Difficulté : ☆☆
Equation de Kepler
Equation de Kepler
L'équation de Kepler est une relation entre l'anomalie excentrique et l'anomalie moyenne, cette page présente un moyen de l'établir. L'aire 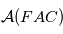 est proportionnelle à l'anomalie moyenne
est proportionnelle à l'anomalie moyenne 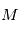 .
.
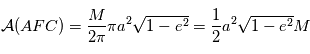
L'ellipse de la trajectoire est obtenue par une affinité sur l'axe 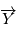 de rapport
de rapport 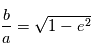 . Donc
. Donc
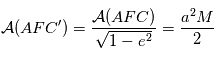
Par ailleurs en notant 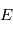 l'angle
l'angle 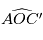
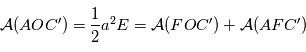
L'aire du triangle 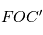 s'obtient facilement car
s'obtient facilement car 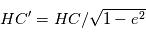
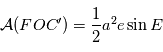
On a finalement l'équation de Kepler
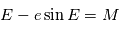
Cette équation est "transcendante", en conqéquence il n'existe pas d'expression analytique de 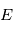 en fonction de
en fonction de 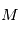 . Cependant, on peut développer
. Cependant, on peut développer 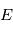 en puissances de
en puissances de 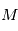 .
.
Anomalies
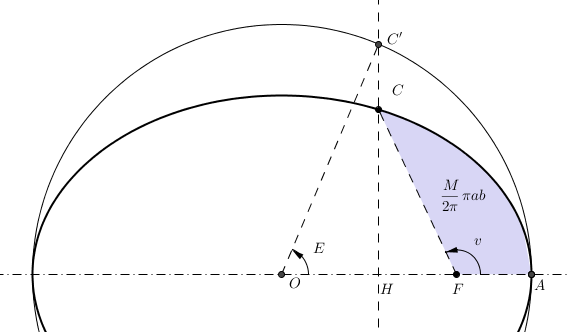
Représentation de l'anomalie vraie
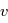
, excentrique
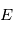
et moyenne
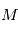
.
Solutions en fonction du temps
Changement de référentiel
Conclusion pour le problème à deux corps
Dans un référentiel galiléen quelconque de centre 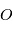 , le mouvement de l'étoile
, le mouvement de l'étoile 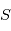 en fonction du temps peut s'écrire:
en fonction du temps peut s'écrire:
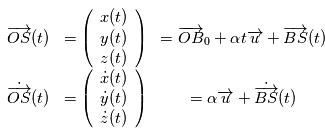
Où 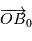 est la position du barycentre
est la position du barycentre 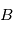 du système {Etoile, Planète} à
du système {Etoile, Planète} à 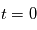 ,
, 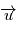 est la direction du mouvement de
est la direction du mouvement de 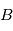 et
et 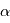 son module.
son module.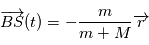 où
où 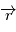 vérifiel'équation de Newton
vérifiel'équation de Newton 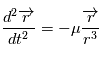 , qui est une équation différentielle de degré deux sur l'espace. Lorsque
, qui est une équation différentielle de degré deux sur l'espace. Lorsque 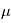 est fixé et la position et la vitesse à
est fixé et la position et la vitesse à 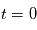 ,
, 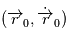 sont connus, la position et la vitesse sont données par le flot:
sont connus, la position et la vitesse sont données par le flot: 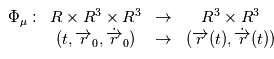 . En d'autres termes, les sept paramètres
. En d'autres termes, les sept paramètres 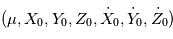 définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple
définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple 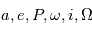 et
et 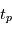 , qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
, qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
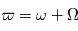 : la longitude du périhélie
: la longitude du périhélie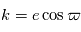
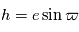
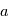 : le demi-grand axe
: le demi-grand axe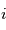 : l'inclinaison
: l'inclinaison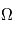 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant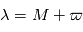 : la longitude
: la longitude
Ces éléments sont des fonctions continues de l'inclinaison et de l'excentricité.
Exercices
Auteur: Nathan Hara
 Bonnes et mauvaises configurations d'observation
Bonnes et mauvaises configurations d'observation
Difficulté : ☆☆
Auteur: Nathan Hara
 Qu'est-ce que les vitesses radiales permettent de mesurer ?
Qu'est-ce que les vitesses radiales permettent de mesurer ?
Difficulté : ☆☆☆
Modèle de la trajectoire
Trajectoire observée depuis le barycentre du système solaire
Trajectoire observée depuis la Terre
Le modèle précédent donne l'évolution de l'étoile dans le repère barycentrique du système solaire (RBSS). Or les observations sont disponibles depuis la Terre. Si 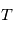 est la position de l'observateur,
est la position de l'observateur, 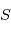 l'étoile cible on a
l'étoile cible on a 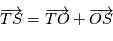
- La mesure de vitesse radiale est celle de
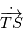 , il faut donc soustraire des observations
, il faut donc soustraire des observations 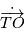
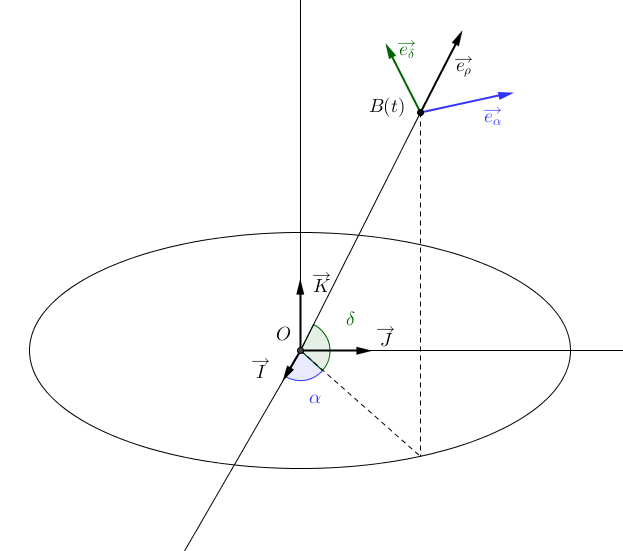
- En astrométrie on observe la projection du mouvement de l'étoile sur la sphère céleste à un certain instant. Non seulement il faut estimer
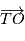 comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure.
comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure.
La dérivée temporelle des vecteur est toujours définie par rapport à un référentiel. Ici la notation 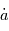 désigne la dérivée temporelle par rapport au RBSS.
désigne la dérivée temporelle par rapport au RBSS.
La détermination de la position du centre de masse de la Terre par rapport au barycentre du système solaire est un sujet à part entière. La trajectoire d'un corps céleste au cours du temps dans un référentiel donné est appelée une éphéméride. Les principaux laboratoires de calcul des éphémérides sont le JPL (NASA) et l'IMCCE (Observatoire de Paris). Les liens envoient sur les générateurs en lignes d'éphémérides respectifs des deux laboratoires. .
Remarque: la procédure de changement de référentiel passe par des changements d'échelle de temps (UTC, UT1, TDB...) qui ne seront pas détaillés ici.
Changement de coordonnées
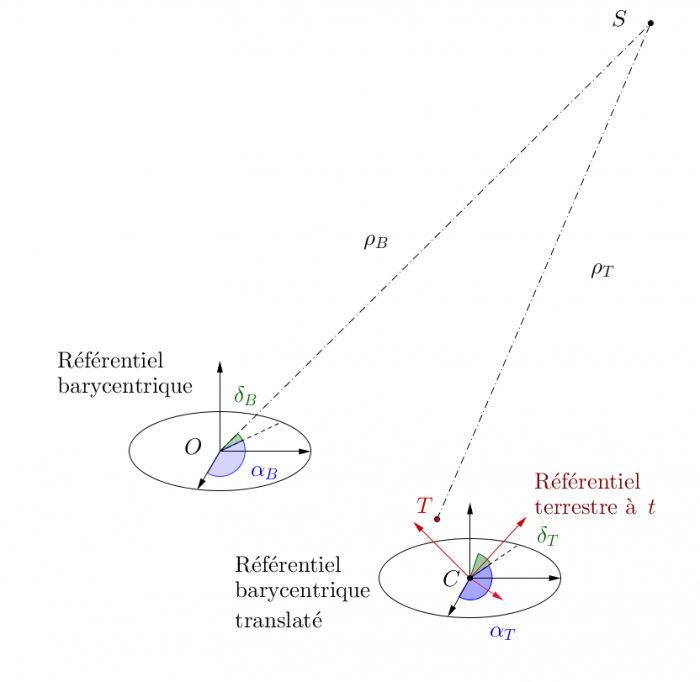
Position de l'étoile en coordonnées sphériques dans le référérentiel barycentrique du système solaire et dans le référentiel translaté au centre de masse de la Terre. Les observations sont disponibles dans le référentiel terrestre, représenté en rouge, qui dépend de l'instant de mesure
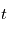
.
Accélération de perspective et changement de parallaxe (astrométrie)
Variation de parallaxe
La variation de parallaxe vaut: 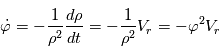 . Comme elle est du deuxième ordre en
. Comme elle est du deuxième ordre en 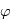 , elle n'est en général pas prise en compte.
, elle n'est en général pas prise en compte.
Changement de coordonnées
Définition de
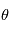
Etoile
Auteur: Nathan Hara & Jacques Laskar
Etoile
L'ajustement des paramètres orbitaux permet de connaître 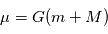 ou bien
ou bien 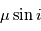 dans le cas des vitesses radiales. Il est impossible de distinguer les masses
dans le cas des vitesses radiales. Il est impossible de distinguer les masses 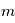 et
et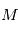 séparément a priori. Cependant, on peut mesurer la masse de l'étoile de sorte à lever l'indetermination.
séparément a priori. Cependant, on peut mesurer la masse de l'étoile de sorte à lever l'indetermination.
La modélisation des étoiles permet de distinguer les effets sur le spectre de la variation de leur flux lumineux de la présence de compagnons planétaires. Ces variations sont modélisées par des variables aléatoires suivant une certaine loi de probabilité, dont l'amplitude varie de plusieurs ordres de grandeur selon le type d'étoile. Plus l'étoile est active, plus l'amplitude du mouvement dû à la planète doit être grande pour distinguer la planète du bruit. En particulier certains types d'étoiles sont trop actives pour pouvoir détecter des potentielles super-Terres compagnon.
La description physique des étoiles est complexe car de nombreux phénomènes, tous interdépendants, ont lieu: convection, radiation, magnétisme... Les modèles utilisés en détection par vitesses radiales comprennent trois phénomènes
- Les ondes de pression se propageant dans les couches extrérieures de l'étoile entrainent des compressions-dilatations de celles-ci, ce qui change la vitesse radiale moyenne observée par rapport à une photosphère statique.Cet effet affecte principalement les observations de vitesses radiales.
- La granulation: phénomène convectif (c'est à dire lié au déplacement de matière dans l'étoile)
- L'activité de l'étoile: la présence de régions sombres ou lumineuses à la période de rotation de l'étoile
L'impact de ces effets sur les mesures n'est pas simple à quantifier. Selon le type d'étoile et les instants d'observations, l'effet peut être très variable. Certains auteurs estiment les incertitudes par des simulations numérique, d'autres par des modèles théoriques. Nous donnons une description qualitative de ces phénomènes et une modélisation possible, mais il faut garder à l'esprit que c'est un sujet de recherche ouvert. Dans le cas des vitesses radiales, ces bruits sont classiquement modélisées par un processus stochastique d'une certaine densité spectrale de puissance, notion importante en statistique, qui est définie dans cette page.
Masse de l'étoile
La mesure de la masse de l'étoile peut se faire de deux manières
- Par ajustement aux observations de modèles théoriques d'intérieurs stellaires.
- Par mesure du mouvement dans un système binaire
Dans le premier cas, si la distance à l'étoile est connue (par exemple par mesure de parallaxe), on peut mesurer sa luminosité intrinsèque 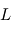 (si on ne connaît pas la distance on ne mesure évidemment que la luminosité apparente). Par son spectre, on peut mesurer sa température effective
(si on ne connaît pas la distance on ne mesure évidemment que la luminosité apparente). Par son spectre, on peut mesurer sa température effective 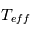 . Des modèles d'intérieurs stellaires permettent ensuite d'évaluer la masse. Cette estimation peut être rafinée avec un modèle d'atmosphère stellaire. On peut alors avoir la gravité à la surface de l'étoile
. Des modèles d'intérieurs stellaires permettent ensuite d'évaluer la masse. Cette estimation peut être rafinée avec un modèle d'atmosphère stellaire. On peut alors avoir la gravité à la surface de l'étoile 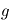 . Comme
. Comme 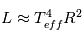 et
et 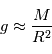 , on peut avoir une estimation de la masse.
, on peut avoir une estimation de la masse.
Dans le cas des étoiles binaires (systèmes de deux étoiles), le spectre présente des raies des deux étoiles. Le mouvement de ces raies se fait à la même fréquence, mais dans des directions opposées (lorsqu'une étoile approche l'autre s'éloigne). La période de ces mouvements est liée à la masse du système par l'équation de Kepler. L'amplitude relative de ces mouvements permet de déterminer la masse des deux étoiles séparément. Comme dans le cas de la détermination des orbites des planètes, la masse n'est connue qu'à un faceteur 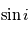 près. Pour lever cette indetermination, il faut déterminer l'inclinaison de l'orbite par rapport à l'observateur
près. Pour lever cette indetermination, il faut déterminer l'inclinaison de l'orbite par rapport à l'observateur 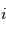 . Si on observe des eclipses (une binaire passe devant l'autre),
. Si on observe des eclipses (une binaire passe devant l'autre), 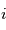
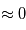 . Si le système n'est pas dans cette configuration, on peut séparer angulairement les deux étoiles par des techniques d'interférométrie.
. Si le système n'est pas dans cette configuration, on peut séparer angulairement les deux étoiles par des techniques d'interférométrie.
Processus stochastique et Densité spectrale de puissance
Processus stochastique
La notion de densité spectrale de puissance (DSP) n'est pas simple à définir, cependant très utilisée dans la littérature de traitement du signal. Nous donnons une définition mathématique pour qu'il n'y ait pas d'ambiguités mais compte tenu de la sophistication des notions introduites, le lecteur pourra se référer à la description qualitative suivante.
La densité spectrale de puissance est une propriété relative à plusieurs variables aléatoires. Les familles de variables aléatoires peuvent par exemple représenter des mesures sur lesquelles on a une incertitude. A chaque instant de mesure on associe une variable alétoire qui a une certaine densité de probabilité. En physique théorique ou en économie, on rencontre des processus stochastiques continus - typiquement le mouvement brownien, qui représente des mouvements d'atomes ou des fluctuations de prix. Formellement, un processus stochastique est une famille de variables aléatoires indexées par un ensemble totalement ordonné 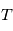 , toutes définies sur le même espace de probabilité (
, toutes définies sur le même espace de probabilité (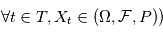 . Dans ce cours on aura seulement besoin de
. Dans ce cours on aura seulement besoin de 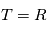 ou
ou 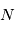 . On note
. On note 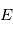 l'espérance mathématique.
l'espérance mathématique.
Dans le cas général, la densité de probabilité de la variable aléatoire 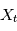 (pour
(pour 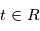 ) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que
) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que 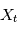 vaut une certaine valeur réelle
vaut une certaine valeur réelle 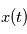 avec la probabilité 1, la DSP en une fréquence
avec la probabilité 1, la DSP en une fréquence 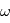 est égale à
est égale à 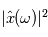 , où
, où 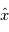 est la transformée de Fourier de
est la transformée de Fourier de 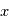 . Si maintenant
. Si maintenant 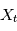 est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de
est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de 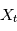 .
.
Pour définir cette notion mathématiquement, on doit d'abord introduire les notions de convergences et intégrales en moyenne quadratique. Pour plus de précision le lecteur peut se référer au cours de Timo Koski à KTH.
Intégrale en moyenne quadratique (Mean Square Integral)
Rappelons d'abord que si 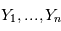 sont des variables aléatoires et
sont des variables aléatoires et 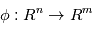 une fonction mesurable alors
une fonction mesurable alors 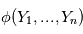 est une variable aléatoire. En particulier, si
est une variable aléatoire. En particulier, si 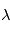 est un scalaire,
est un scalaire, 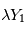 et
et 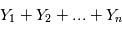 sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
Soit 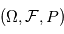 un espace de probabilités, on dit que la suite de variables aléatoires
un espace de probabilités, on dit que la suite de variables aléatoires 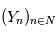 telle que
telle que 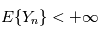 , définies sur cet espace converge en moyenne quadratique si et seulement si:
, définies sur cet espace converge en moyenne quadratique si et seulement si:
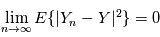
Soit 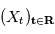 un processus stochastique continu (
un processus stochastique continu (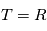 ) tel que chacune des variables aléatoires
) tel que chacune des variables aléatoires 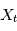 a une espérance finie (
a une espérance finie (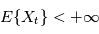 ). L'intégrale en moyenne quadratique du processus
). L'intégrale en moyenne quadratique du processus 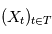 sur l'intervalle
sur l'intervalle ![[a,b]](../pages_ind-vr/equations_etoile/equation44.png) est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
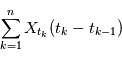
Pour 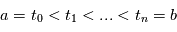 et
et 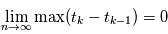 . On la note alors
. On la note alors 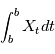 .
.
On définit alors la densité spectrale de puissance comme:
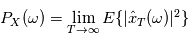
Où 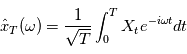
Cette définition un peu complexe peut être vue comme une généralisation de la transformée de Fourier à des processus stochastiques. En effet, lorsque le processus 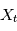 est telle que
est telle que 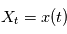 avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors
avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors 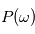 est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle
est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle 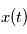 . Dans le cas où les
. Dans le cas où les 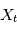 sont aléatoire,
sont aléatoire, 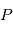 est le carré de la transformée de Fourier "en moyenne" des réalisations de
est le carré de la transformée de Fourier "en moyenne" des réalisations de 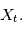 Par exemple si
Par exemple si 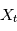 modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant
modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant 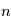 profils de tension
profils de tension 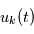 à l'expérience
à l'expérience 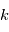 (des réalisations du processus stochastique
(des réalisations du processus stochastique 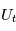 ), la moyenne des carrés du module des transformées de Fourier des
), la moyenne des carrés du module des transformées de Fourier des 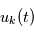 notée
notée 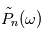 sera approximativement égal à
sera approximativement égal à 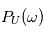 . Si le nombre d'expérience
. Si le nombre d'expérience 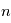 tend vers l'infini
tend vers l'infini 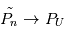 en norme 2.
en norme 2.
Dans le cas d'un processus stationnaire discret (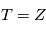 ), on peut directement définir
), on peut directement définir 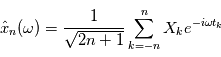 et
et 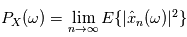 .
.
Granulation
Le phénomène de granulation est lié à la convection du gaz dans l'étoile. La lumière rayonnée par le gaz chaud remontant à la surface va vers l'observateur, la longueur d'onde reçue est donc décalée vers le bleu. En rayonnant, le gaz se refroidit, puis repart vers le centre de l'étoile. Etant moins chaud, il émet moins de lumière, si bien que la lumière est globalement décalée vers le bleu. Ce phénomène est variable dans le temps, donc le décalage vers le bleu aussi. Cette variation peut apparaître dans le spectre et créer des fréquences parasites. La nature aléatoire du phénomène fait que même après ajustement, il reste un bruit résiduel. Pour une étoile de type solaire, il est de l'ordre de 0.5 - 1 m/s sur une observation.
La granulation est en général modélisée par un processus stochastique dits de bruits en créneaui (popcorn noise ou burst noise en anglais). Il s'agit de processus stochastiques pouvant prendre deux valeurs, par exemple -1 ou 1 avec une probabilité de changement suivant une loi de Poisson (loi exponentielle). Si à 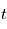 la valeur passe de 1 à -1, la densité de probabilité pour que la valeur passe à 1 à
la valeur passe de 1 à -1, la densité de probabilité pour que la valeur passe à 1 à 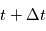 est
est 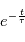 où
où 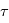 est un réel positif. Pour les vitesses radiales, la densité spectrale de puissance de ces bruits peut être modélisée par::
est un réel positif. Pour les vitesses radiales, la densité spectrale de puissance de ces bruits peut être modélisée par::
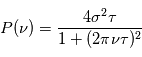
Cette modélisation, due à Harvey (1985) a depuis été revue et d'autres densités spectrales de puissances ont été proposée à partir de simulations 3d de convection au sein d'une étoile. En pratique, le bruit dû à la granulation apparaitra comme un signal périodique de l'ordre de cinq minutes. Cependant, on observe aussi des phénomènes appelés meso-granulation et super-granulation sur des échelles de temps plus longues. La contribution totale de ces bruits est:
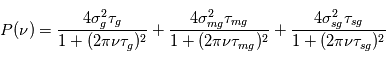
Où les indices g, mg et sg se réfèrent respectivement à la granulation, la méso granulation et la super-granulation. En anticipant un peu sur le troisième chapitre, lorsque ces bruits sont pris en compte, les valeurs des 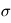 et
et 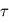 sont ajustés sur le spectre de puissance du signal.
sont ajustés sur le spectre de puissance du signal.
Activité magnétique
La formation d'arcs de champ magnétique à la surface de l'étoile inhibe le mouvement des particules, donc réduit la température et provoque donc des tâches sombres. Cet effet à des effets à court termes (à la fréquence de rotation de l'étoile 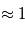 mois), et à plus long terme à travers des cycles d'activité magnétique.
mois), et à plus long terme à travers des cycles d'activité magnétique.
A court trerme, la tache introduit une dissymétrie entre la partie de l'étoile tournant vers l'observateur, et la partie s'en éloignant, ce qui engendre un décalage du spectre mesuré. D'autre part, la tache engendre un déplacement du photocentre de l'étoile périodique, pouvant être confondu avec la présence d'une planète. Pour éviter ces confusions, on estime la période de rotation de l'étoile par spectroscopie, et on ajuste des sinusoïdes à cette période et ses premières harmoniques.
L'activité magnétique peut se mesurer à travers divers indicateurs, dont on analyse les corrélations.
Toujours selon le modèle de Harvey (1985), la densité spectrale de puissance du bruit de vitesse radiale induit par une tache solaire est:
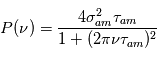
Effet de la rotation de l'étoile sur le spectre
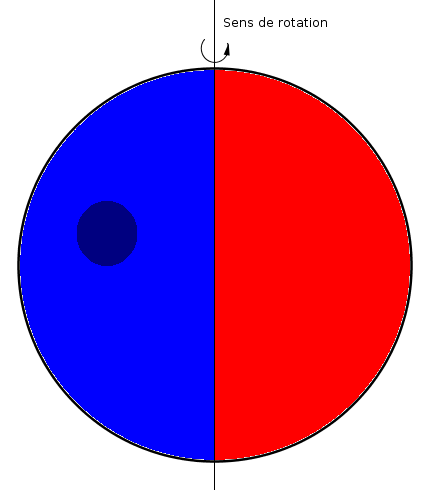
La lumière provenant de la moitié de l'étoile ayant un mouvement vers l'observateur est décalé vers les hautes fréquences (vers le bleu). L'autre moitié est décalée vers les basses fréquences (vers le rouge). Dans l'hypothèse où l'étoile est sphérique, et a une luminosité identique partout sur sa surface, le décalage vers le rouge et celui vers le bleu ne fait qu'élargir les raies spectrales. Si une tache est présente, ici sur la partie bleue, la symétrie est brisée et le déficit de lumière entraine un décalage du spectre vers le rouge.
Oscillations radiales (vitesses radiales)
Des inhomogénéités de densité dues aux mouvements convectifs font que des ondes mécaniques se propagent au sein des étoiles. Certaines de ces ondes sont radiales, ce qui provoque un mouvement d'ensemble de la photosphère qui a une signature sur le décalage du spectre mesuré. L'étude de ces ondes est un domaine de la physique stellaire appelé "astérosismologie". Etant donné que la théorie est accessible au niveau licence, nous en donnons des principes généraux.
La théorie procède comme suit: on écrit localement 1) l'équation du mouvement linéarisée au premier ordre au voisinage d'un état d'équilibre, 2) la conservation de la masse ou équation de continuité, 3) l'équation de Poisson, liant le potentiel gravitationnel et la densité, 4) Le premier principe de la thermodynamique. On néglige l'effet du champ magnétique. En général, on fait l'hypothèse que le terme de transfert thermique dans le 1er principe est nul.
Perturbations atmosphériques
Vitesses radiales
L'atmosphère peut influencer la mesure de vitesses radiales de deux manières:
- Par atténuation de l'intensité, ce qui augmente le bruit de photon
- Par la modification du contenu spectral du signal
La présence de lignes spectrales d'émission ou d'absorption est difficile à corriger. C'est pourquoi on ne considère que des plages de fréquences où l'intensité des raies atmosphériques est inférieure à 1/10000 de l'intensité de la cible. De plus, la réponse de l'atmosphère dépend de la longueur d'onde. Le spectre obtenu est pondéré de sorte à corriger ces inhomogénéités.
Récapitulation
Les effets expliqués précédemment sont pour la plupart périodiques, donc peuvent être confondus avec le signal d'une planète. Le tableau suivant récapitule ces effets, leurs amplitudes et périodes typiques pour des étoiles de type solaire.
Effets physiques
| Effet | Description | Amplitude (vitesse radiale) | Amplitude (astrométrie) | Echelle de temps |
|---|
| Mouvement des planètes | Le mouvement des planètes autour de
l'étoile engendre un mouvement périodique | 1 cm/s - 200 m/s | Terre: 0.3, 0.03 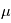 as
Jupiter: 500, 20 as
Jupiter: 500, 20 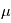 as
à 1 et 10 parsec resp. as
à 1 et 10 parsec resp. | de un jour à plusieurs centaines d'années |
| Mouvement propre | Mouvement rectiligne uniforme | Dizaines de kilomètres par seconde | 10 - 1000 mas pour les étoiles observables | Mouvement non périodique |
| Taches | La présence de taches sombres ou lumineuses
dues à l'activité magnétique provoque une
disymétris entre la luminosité de la partie bleue
et la partie rouge de l'étoile, engendrant un décalage
du spectre ou du photocentre. | 1 m/s | Avec ces trois effets,
0.5 - 10 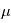 UA UA | Période de rotation de l'étoile (quelques jours) |
| Activité magnétique (long terme) | Le nombre de tâche à la surface de l'étoile peut varier
de quelques unes à plusieurs centaines. Par exemple le
soleil a une périodicité de 11 ans. L'effet
précédent est modulé par ces variations à long terme. | 10 m/s | 1 - 10 ans |
| Granulation | Le mouvement convectif à l'intérieur de l'étoile provoque
un mouvement du gaz dans la photosphère | 0.5 - 1 m/s | Granulation: quelques minutes, mesogranulation: |
| Oscillations radiales (p-modes) | La propagations d'ondes acoustiques dans le manteau
de l'étoile entraîne une oscillation de celui-ci | 0.5 - 1 m/s | inconnu |
5 - 10 minutes |
| Système multiple | La présence d'autres étoiles orbitant autour de l'étoile
cible engendre un mouvement décrit par les mêmes
équations que celles utilisées pour les planètes. Les autres
étoiles étant beaucoup plus massives que des planètes,
l'effet est plus important. | 1 - 30 km/s | 0.1 - 1 as/an | 10 - 100 ans |
effets observationnels
| Effet | Description | Amplitude (vitesse radiale) | Amplitude (astrométrie) | Echelle de temps |
|---|
| Mouvement de l'observateur dans le RBSS | Comme l'observateur est en mouvement dans un référentiel
galiléen, | 30 km/s (après soustraction, on a une erreur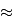 0.5 m/s
à cause des incertitudes sur la rotation de la Terre
et les éphémérides) 0.5 m/s
à cause des incertitudes sur la rotation de la Terre
et les éphémérides) | 0.01 - 0.1 as/an | Une année |
| Perturbations atmosphériques | La présence de raies spectrales atmosphériques peut perturber
les observations par vitesses radiale, et les turbulences dévient
les fronts d'ondes, engendrant un déplacement apparent des sources. | 0.5 m/s | 1 mas | Quelques minutes |
Réponses aux exercices
pages_ind-vr/exercice5.html
Exercice
'Bonnes et mauvaises configurations d'observation'
pages_ind-vr/exercice5.html
Exercice
'Qu'est-ce que les vitesses radiales permettent de mesurer ?'
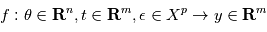 , où
, où 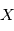 désigne un espace de variables aléatoires, qui donne des observations
désigne un espace de variables aléatoires, qui donne des observations 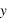 en fonction d'instants d'observation
en fonction d'instants d'observation 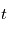 , d'erreurs alétoires
, d'erreurs alétoires 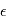 et de paramètre du modèle
et de paramètre du modèle 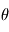 incluant masse de la planète, de l'étoile, paramètres de l'orbites, etc. qui seront précisés. En l'occurrence, l'erreur est bien représentée par un "bruit additif", c'est à dire les observations
incluant masse de la planète, de l'étoile, paramètres de l'orbites, etc. qui seront précisés. En l'occurrence, l'erreur est bien représentée par un "bruit additif", c'est à dire les observations 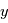 sont de la forme
sont de la forme 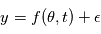 , où
, où 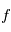 désigne une fonction modélisant la physique du phénomène observée, celle qui donnerait les observations "parfaites", sans aucune source d'erreur aléatoire. L'erreur
désigne une fonction modélisant la physique du phénomène observée, celle qui donnerait les observations "parfaites", sans aucune source d'erreur aléatoire. L'erreur 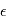 modélise tous les phénomènes aléatoires intervenant dans les mesures. Selon la distinction adoptée ici, les paramètres du modèle peuvent inclure une source indésirable mais non aléatoire.
modélise tous les phénomènes aléatoires intervenant dans les mesures. Selon la distinction adoptée ici, les paramètres du modèle peuvent inclure une source indésirable mais non aléatoire.
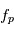 avec une modélisation physique. La modélisation la plus précise, utilisant tout ce que l'on sait de la physique serait ici inutilement complexe, car compte tenu des erreurs de mesures la différence avec certains modèles plus simples serait si faible qu'il serait impossible de la détecter avec un niveau de confiance acceptable. Le niveau de précision du modèle présenté ici est couramment utilisé par les observateurs.
avec une modélisation physique. La modélisation la plus précise, utilisant tout ce que l'on sait de la physique serait ici inutilement complexe, car compte tenu des erreurs de mesures la différence avec certains modèles plus simples serait si faible qu'il serait impossible de la détecter avec un niveau de confiance acceptable. Le niveau de précision du modèle présenté ici est couramment utilisé par les observateurs.
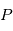 (planète) et
(planète) et 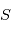 (pour "star" de sorte à éviter un conflit de notation avec l'anomalie excentrique
(pour "star" de sorte à éviter un conflit de notation avec l'anomalie excentrique 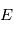 ) de masses respectives
) de masses respectives 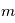 et
et 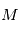 et
et 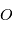 l'origine d'un repère Galiléen. Le principe fondamental de la dynamique s'écrit:
l'origine d'un repère Galiléen. Le principe fondamental de la dynamique s'écrit:
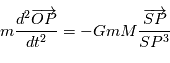 où
où 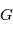 est la constante universelle de gravitation.. En posant
est la constante universelle de gravitation.. En posant 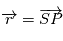 et
et 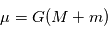 on obtient:
on obtient:
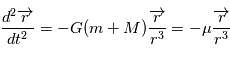
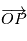 et
et 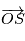 par la relation
par la relation 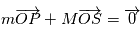 .
.
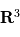 . Pour la résoudre il faut trouver six quantités conservées au cours du mouvement (ou intégrales premières du mouvement) indépendantes. En l'occurrence on peut facilement montrer que deux vecteurs sont conservés au cours du mouvement (ce qui fait deux fois trois composantes, on a bien six scalaires conservés).
Notons
. Pour la résoudre il faut trouver six quantités conservées au cours du mouvement (ou intégrales premières du mouvement) indépendantes. En l'occurrence on peut facilement montrer que deux vecteurs sont conservés au cours du mouvement (ce qui fait deux fois trois composantes, on a bien six scalaires conservés).
Notons 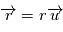 , où
, où 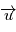 est un vecteur unitaire (et donc
est un vecteur unitaire (et donc 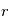 est la norme de
est la norme de 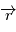 ) et
) et 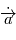 la dérivée par rapport au temps d'un vecteur
la dérivée par rapport au temps d'un vecteur 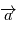 .
On a la conservation du moment cinétique par unité de masse
.
On a la conservation du moment cinétique par unité de masse 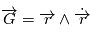 et du vecteur excentricité
et du vecteur excentricité 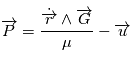 au cours du mouvement c'est à dire leur dérivée temporelle est nulle
au cours du mouvement c'est à dire leur dérivée temporelle est nulle
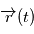 une solution de l'équation de Newton. Alors
une solution de l'équation de Newton. Alors 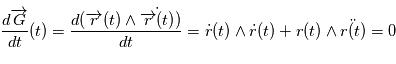 car d'après l'équation de Newton,
car d'après l'équation de Newton, 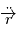 est colinéaire à
est colinéaire à 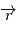 . D'autre part,
. D'autre part, 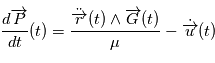 , or
, or
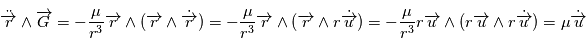
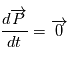 .
.
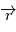 .
.
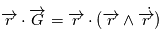 et comme
et comme 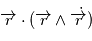 est un produit mixte, il est invariant par permutation circulaire:
est un produit mixte, il est invariant par permutation circulaire: 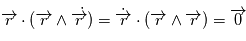 car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur
car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur 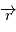 est orthogonal à
est orthogonal à 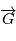 à tout instant, autrement dit le mouvement est dans un plan orthogonal à
à tout instant, autrement dit le mouvement est dans un plan orthogonal à 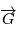 .
.
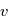 l'angle entre
l'angle entre 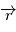 et
et 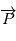 et posons
et posons 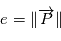 . Alors comme
. Alors comme 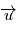 est unitaire,
est unitaire, 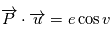 d'autre part en remplaçant
d'autre part en remplaçant 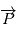 par sa définition, on a
par sa définition, on a 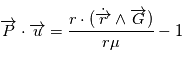 et comme
et comme 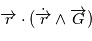 est un produit mixte,
est un produit mixte, 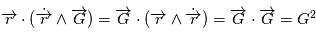 . où
. où 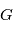 est la norme de
est la norme de 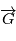 . On obtient alors
. On obtient alors 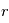 en fonction de
en fonction de 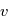 :
:
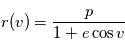
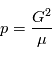 , qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de
, qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de 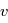 , appelée
, appelée 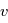 et le temps.
On sait que lorsque
et le temps.
On sait que lorsque 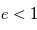 , il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que
, il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que 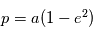 où
où 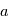 est le demi-grand axe de l'ellipse. Si
est le demi-grand axe de l'ellipse. Si 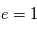 ou
ou 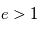 , la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
, la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
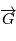 , et le vecteur
, et le vecteur 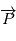 est parallèle à
est parallèle à 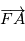 . Notons
. Notons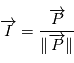 et
et 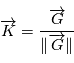 . On introduit un vecteur
. On introduit un vecteur 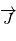 de sorte que
de sorte que 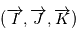 forme une base orthonormale.
forme une base orthonormale.

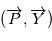
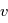 , angle entre le vecteur excentricité et le vecteur
, angle entre le vecteur excentricité et le vecteur 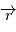 .
.
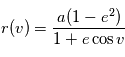
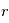 en fonction du temps on va introduire successivement deux variables,
en fonction du temps on va introduire successivement deux variables, 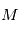 et
et 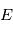 appelées respectivement '
appelées respectivement '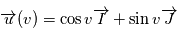 , donc
, donc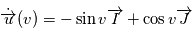 en remplaçant dans,
en remplaçant dans, 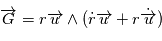 on obtient:
on obtient:
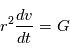
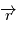 balaie les aires à vitesse constant
balaie les aires à vitesse constant 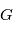 . En particulier l'aire totale de l'ellipse est parcourue en un certain temps
. En particulier l'aire totale de l'ellipse est parcourue en un certain temps 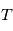 fixe: le mouvement est périodique. L'aire de l'ellipse vaut:
fixe: le mouvement est périodique. L'aire de l'ellipse vaut:
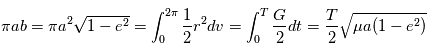
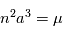 avec
avec 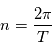 . On définit alors l'
. On définit alors l'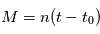 où
où 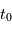 est le temps de passage au périastre (
est le temps de passage au périastre (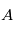 sur la figure), qui est proportionnelle à l'aire
sur la figure), qui est proportionnelle à l'aire 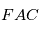 (voir figure).
(voir figure).
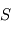 et
et 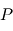 de masses respectives
de masses respectives 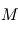 et
et 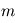 . On pose
. On pose 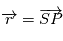 ,
, 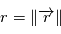 et
et 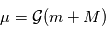 où
où 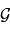 est la constante universelle de gravitation.
est la constante universelle de gravitation.
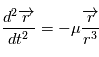
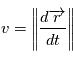 . Déduire du théorème de l'énergie mécanique que
. Déduire du théorème de l'énergie mécanique que 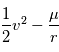 est une quantité constante au cours du mouvement
est une quantité constante au cours du mouvement 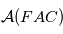 est proportionnelle à l'anomalie moyenne
est proportionnelle à l'anomalie moyenne 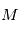 .
.
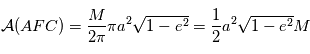
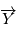 de rapport
de rapport 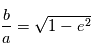 . Donc
. Donc
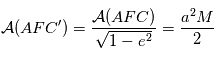
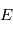 l'angle
l'angle 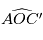
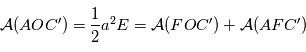
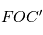 s'obtient facilement car
s'obtient facilement car 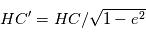
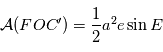
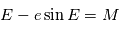
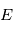 en fonction de
en fonction de 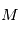 . Cependant, on peut développer
. Cependant, on peut développer 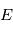 en puissances de
en puissances de 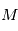 .
.

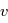 , excentrique
, excentrique 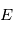 et moyenne
et moyenne 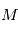 .
.
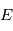 et
et 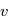 , ce qui s'obtient aisément en exprimant la position
, ce qui s'obtient aisément en exprimant la position 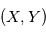 de
de 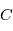 dans le plan
dans le plan 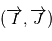 :
:
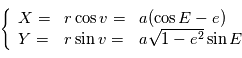
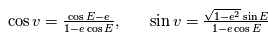
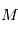 en fonction de
en fonction de 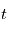 puis
puis 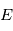 en fonction de
en fonction de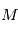 on a la position du corps à un instant quelconque. En ce qui concerne l'astrométrie, on peut s'arrêter aux équations ci-dessus et simplement faire un changement de référentiel, c'ést à dire exprimer la projection de
on a la position du corps à un instant quelconque. En ce qui concerne l'astrométrie, on peut s'arrêter aux équations ci-dessus et simplement faire un changement de référentiel, c'ést à dire exprimer la projection de 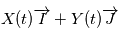 sur la sphère céleste et choisir un jeu de paramètres
sur la sphère céleste et choisir un jeu de paramètres 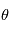 à ajuster. Pour les vitesses radiales nous avons besoin de
à ajuster. Pour les vitesses radiales nous avons besoin de 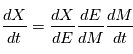 . En dérivant l'équation de Kepler par rapport à
. En dérivant l'équation de Kepler par rapport à 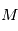 on obtient:
on obtient:
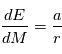
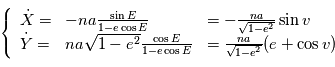
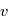 en fonction de
en fonction de 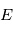 . Les expressions ci-dessus suffisent. Pour mémoire, en remplaçant
. Les expressions ci-dessus suffisent. Pour mémoire, en remplaçant 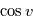 dans la formule trigonométrique
dans la formule trigonométrique 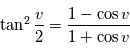 , on obtient:
, on obtient:
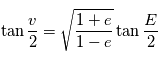
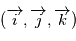 où
où 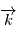 est la direction d'observation et
est la direction d'observation et 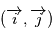 sont choisis de sorte que le repère est orthonormé direct. Le repère
sont choisis de sorte que le repère est orthonormé direct. Le repère 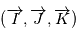 est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
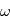 d'axe
d'axe 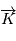 (parallèle au moment cinétique), cet angle est appelé
(parallèle au moment cinétique), cet angle est appelé 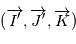 .
. 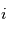 d'axe
d'axe 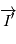 , c'est l'
, c'est l' 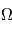 d'axe
d'axe 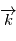 , c'est l'
, c'est l'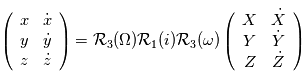
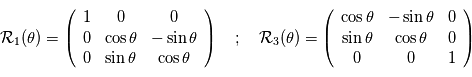
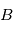 le barycentre du système {planète+étoile}, on note
le barycentre du système {planète+étoile}, on note 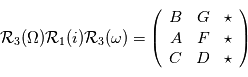 où
où 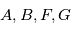 sont appelées les
sont appelées les 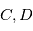 n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que
n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que 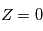 , ils n'apparaissent jamais dans les calculs
, ils n'apparaissent jamais dans les calculs
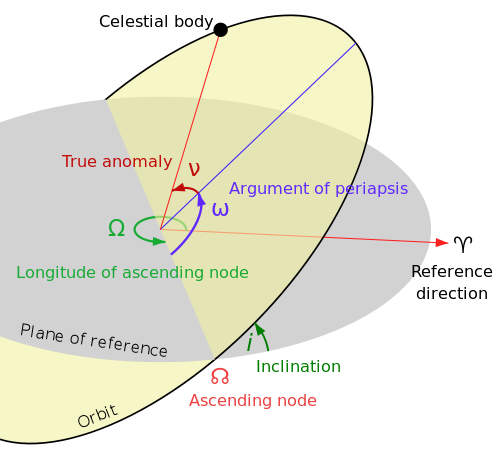
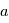 : le demi-grand axe
: le demi-grand axe 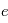 : l'excentricité
: l'excentricité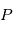 : la période
: la période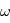 : l'argument du périastre
: l'argument du périastre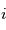 : l'inclinaison
: l'inclinaison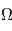 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant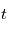 donné, il faut de plus connaître l'instant de son passage au périastre
donné, il faut de plus connaître l'instant de son passage au périastre 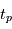 . On peut alors calculer
. On peut alors calculer 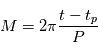 connaisant
connaisant 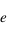 on peut calculer l'anomalie excentrique
on peut calculer l'anomalie excentrique 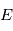 par l'équation de Kepler, puis l'anomalie vraie
par l'équation de Kepler, puis l'anomalie vraie 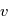 . On en déduit la position sur l'ellipse par l'équation donnée page
. On en déduit la position sur l'ellipse par l'équation donnée page 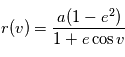 . Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.
. Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.
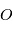 , le mouvement de l'étoile
, le mouvement de l'étoile 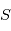 en fonction du temps peut s'écrire:
en fonction du temps peut s'écrire:
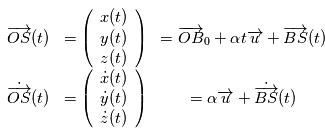
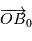 est la position du barycentre
est la position du barycentre 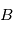 du système {Etoile, Planète} à
du système {Etoile, Planète} à 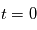 ,
, 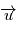 est la direction du mouvement de
est la direction du mouvement de 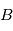 et
et 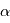 son module.
son module.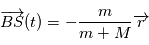 où
où 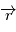 vérifie
vérifie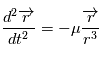 , qui est une équation différentielle de degré deux sur l'espace. Lorsque
, qui est une équation différentielle de degré deux sur l'espace. Lorsque 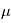 est fixé et la position et la vitesse à
est fixé et la position et la vitesse à 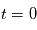 ,
, 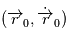 sont connus, la position et la vitesse sont données par le flot:
sont connus, la position et la vitesse sont données par le flot: 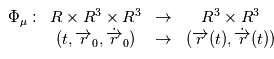 . En d'autres termes, les sept paramètres
. En d'autres termes, les sept paramètres 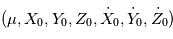 définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple
définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple 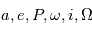 et
et 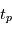 , qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
, qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
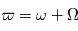 : la longitude du périhélie
: la longitude du périhélie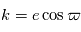
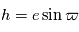
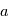 : le demi-grand axe
: le demi-grand axe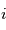 : l'inclinaison
: l'inclinaison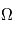 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant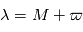 : la longitude
: la longitude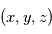 où la direction
où la direction 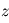 est selon la droite observateur - étoile. Avec les notations des pages précédentes, pour quelles valeurs de l'inclinaison
est selon la droite observateur - étoile. Avec les notations des pages précédentes, pour quelles valeurs de l'inclinaison 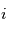 les observations de vitesses radiales ne donnent aucune information sur le système ? lequelles rendent la configuration optimale ?
Même question pour les angles
les observations de vitesses radiales ne donnent aucune information sur le système ? lequelles rendent la configuration optimale ?
Même question pour les angles 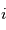 et
et 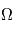 en astrométrie.
en astrométrie.
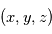 où la direction
où la direction 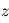 est selon la droite observateur - étoile. On note
est selon la droite observateur - étoile. On note 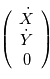 les composantes du mouvement dans le plan orbital.
Calculer la composante du mouvement de l'étoile selon la direction d'observation. On mettra les observations sous la forme
les composantes du mouvement dans le plan orbital.
Calculer la composante du mouvement de l'étoile selon la direction d'observation. On mettra les observations sous la forme
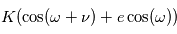 , où
, où 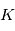 est une constante à déterminer.
Quels paramètres de l'orbite peut-on observer par vitesse radiale ? Montrer en particulier qu'on ne peut pas déterminer la masse exacte de la planète.
est une constante à déterminer.
Quels paramètres de l'orbite peut-on observer par vitesse radiale ? Montrer en particulier qu'on ne peut pas déterminer la masse exacte de la planète.
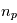 planètes orbitent autour de l'étoile.
planètes orbitent autour de l'étoile.
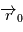 et
et 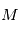 respectivement la position et la masse de l'étoile et
respectivement la position et la masse de l'étoile et 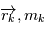 ,
, 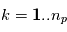 les positions et masses des
les positions et masses des 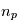 planètes , les équations de la mécanique (classique) dans le référentiel barycentrique de ce système sont:
planètes , les équations de la mécanique (classique) dans le référentiel barycentrique de ce système sont:
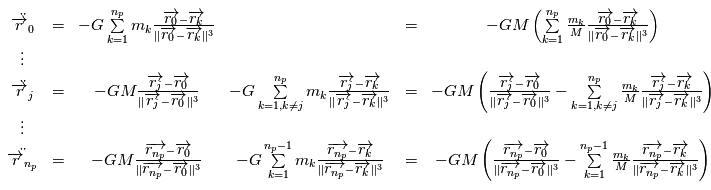
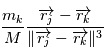 , c'est à dire l'intéraction entre les planètes, on obtient:
, c'est à dire l'intéraction entre les planètes, on obtient:
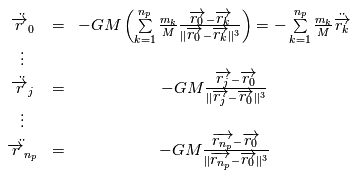
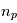 problèmes à deux corps associés à chacune des planètes, par
problèmes à deux corps associés à chacune des planètes, par 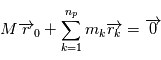 (dont la première équation du système ci-dessus est la dérivée seconde) on obtient le mouvement de l'étoile. Le modèle de trajectoire complet dans un référentiel galiléen est:
(dont la première équation du système ci-dessus est la dérivée seconde) on obtient le mouvement de l'étoile. Le modèle de trajectoire complet dans un référentiel galiléen est:
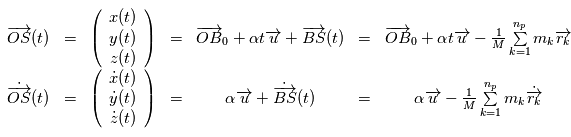
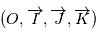 , que l'on munit d'un repère de coordonnées sphériques
, que l'on munit d'un repère de coordonnées sphériques 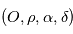 repérant l'étoile
repérant l'étoile 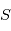 . Supposons que l'observateur est situé en
. Supposons que l'observateur est situé en 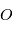 . A un instant
. A un instant 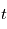 il mesure:
il mesure:
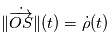
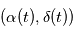 dans le cas de mesures astrométriques
dans le cas de mesures astrométriques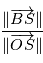 ,
, 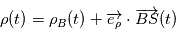 ,
, 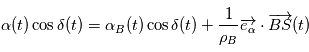 , de même
, de même 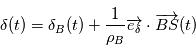 (à faire en exercice).
Supposons que
(à faire en exercice).
Supposons que 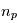 planètes indéxées par
planètes indéxées par 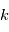 gravitent autour de l'étoile en
gravitent autour de l'étoile en 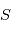 et
et 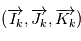 le repère orbital de la planète
le repère orbital de la planète 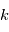 . On projette le mouvement
. On projette le mouvement 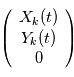 dans le repère orthonormé direct
dans le repère orthonormé direct 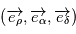 associé aux coordonnées sphériques
associé aux coordonnées sphériques 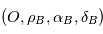 (voir figure). Avec les notations de la page
(voir figure). Avec les notations de la page 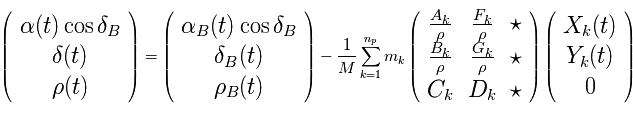
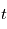 .
.
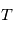 est la position de l'observateur,
est la position de l'observateur, 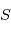 l'étoile cible on a
l'étoile cible on a 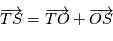
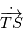 , il faut donc soustraire des observations
, il faut donc soustraire des observations 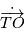
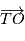 comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure.
comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure. 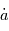 désigne la dérivée temporelle par rapport au RBSS.
désigne la dérivée temporelle par rapport au RBSS.
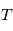 par rapport au barycentre du système solaire peut se décomposer en
par rapport au barycentre du système solaire peut se décomposer en 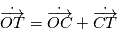 . La partie
. La partie 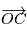 est donné par les éphémérides, comme expliqué plus haut. La correction de la deuxième partie est essentielle: l'observateur parcourt deux fois le rayon terrestre en une nuit, ce qui donne une vitesse d'environ 300 m/s. Si
est donné par les éphémérides, comme expliqué plus haut. La correction de la deuxième partie est essentielle: l'observateur parcourt deux fois le rayon terrestre en une nuit, ce qui donne une vitesse d'environ 300 m/s. Si 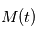 désigne la matrice de changement de repère entre le référentiel lié à la Terre et le référentiel barycentrique du système solaire, on a
désigne la matrice de changement de repère entre le référentiel lié à la Terre et le référentiel barycentrique du système solaire, on a 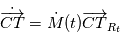 où
où 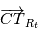 désigne la position de l'observateur dans le référentiel terrestre.
désigne la position de l'observateur dans le référentiel terrestre.
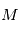 est aussi un sujet à part entière, appelé "rotation de la Terre". Les paramètres de rotations officiels sont donnés par le
est aussi un sujet à part entière, appelé "rotation de la Terre". Les paramètres de rotations officiels sont donnés par le 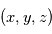 la position de la Terre dans le RBS. En exprimant
la position de la Terre dans le RBS. En exprimant 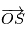 dans le RBSS de deux manières on obtient une relation entre les coordonnées
dans le RBSS de deux manières on obtient une relation entre les coordonnées 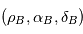 et
et 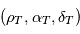 :
:
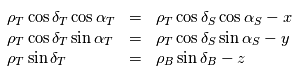
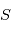 est suffisamment loin, ces expressions différenciées au voisinage de
est suffisamment loin, ces expressions différenciées au voisinage de 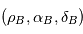 donnent au premier ordre en
donnent au premier ordre en 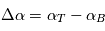 ,
, 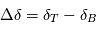 et
et 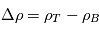
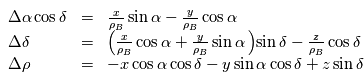
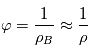 la parallaxe de l'étoile (en général notée
la parallaxe de l'étoile (en général notée 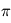 ou
ou 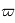 , qui sont des symboles déjà utilisés dans le cours). Elle considérée comme constante au cours des observations et est ajustée aux observations en astrométrie.
, qui sont des symboles déjà utilisés dans le cours). Elle considérée comme constante au cours des observations et est ajustée aux observations en astrométrie.

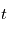 .
.
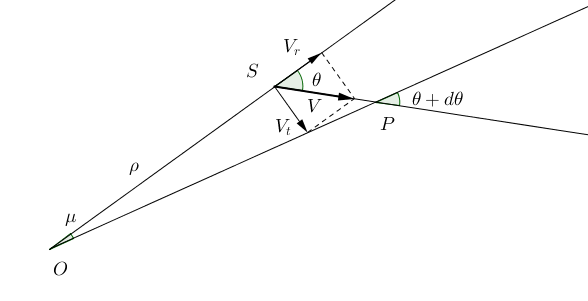
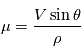 où
où 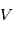 est la vitesse du système observé,
est la vitesse du système observé, 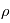 la distance entre l'observateur et le système,
la distance entre l'observateur et le système, 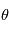 est l'angle entre la ligne de visée et la vitesse du système observé.
Nous supposons que les mesures astrométriques sont sur un plan. Cependant, on mesure la projection du mouvement sur une sphère, donc
est l'angle entre la ligne de visée et la vitesse du système observé.
Nous supposons que les mesures astrométriques sont sur un plan. Cependant, on mesure la projection du mouvement sur une sphère, donc 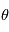 n'est pas constant au cours du temps. En dérivant par rapport au temps, comme
n'est pas constant au cours du temps. En dérivant par rapport au temps, comme 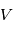 est constant:
est constant:
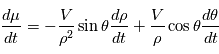
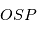 que
que 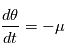 et
et 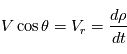 . D'où:
. D'où:
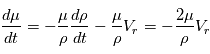
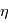 , où le mouvement angulaire sur la sphère céleste est donné par
, où le mouvement angulaire sur la sphère céleste est donné par 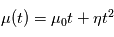 .
.
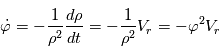 . Comme elle est du deuxième ordre en
. Comme elle est du deuxième ordre en 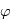 , elle n'est en général pas prise en compte.
, elle n'est en général pas prise en compte.

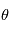
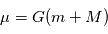 ou bien
ou bien 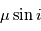 dans le cas des vitesses radiales. Il est impossible de distinguer les masses
dans le cas des vitesses radiales. Il est impossible de distinguer les masses 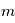 et
et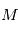 séparément a priori. Cependant, on peut mesurer la masse de l'étoile de sorte à lever l'indetermination.
séparément a priori. Cependant, on peut mesurer la masse de l'étoile de sorte à lever l'indetermination.
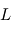 (si on ne connaît pas la distance on ne mesure évidemment que la luminosité apparente). Par son spectre, on peut mesurer sa température effective
(si on ne connaît pas la distance on ne mesure évidemment que la luminosité apparente). Par son spectre, on peut mesurer sa température effective 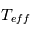 . Des modèles d'intérieurs stellaires permettent ensuite d'évaluer la masse. Cette estimation peut être rafinée avec un modèle d'atmosphère stellaire. On peut alors avoir la gravité à la surface de l'étoile
. Des modèles d'intérieurs stellaires permettent ensuite d'évaluer la masse. Cette estimation peut être rafinée avec un modèle d'atmosphère stellaire. On peut alors avoir la gravité à la surface de l'étoile 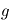 . Comme
. Comme 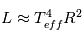 et
et 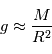 , on peut avoir une estimation de la masse.
, on peut avoir une estimation de la masse.
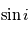 près. Pour lever cette indetermination, il faut déterminer l'inclinaison de l'orbite par rapport à l'observateur
près. Pour lever cette indetermination, il faut déterminer l'inclinaison de l'orbite par rapport à l'observateur 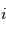 . Si on observe des eclipses (une binaire passe devant l'autre),
. Si on observe des eclipses (une binaire passe devant l'autre), 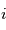
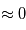 . Si le système n'est pas dans cette configuration, on peut séparer angulairement les deux étoiles par des techniques d'interférométrie.
. Si le système n'est pas dans cette configuration, on peut séparer angulairement les deux étoiles par des techniques d'interférométrie.
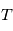 , toutes définies sur le même espace de probabilité (
, toutes définies sur le même espace de probabilité (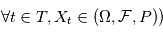 . Dans ce cours on aura seulement besoin de
. Dans ce cours on aura seulement besoin de 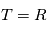 ou
ou 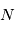 . On note
. On note 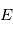 l'espérance mathématique.
l'espérance mathématique.
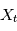 (pour
(pour 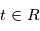 ) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que
) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que 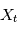 vaut une certaine valeur réelle
vaut une certaine valeur réelle 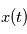 avec la probabilité 1, la DSP en une fréquence
avec la probabilité 1, la DSP en une fréquence 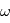 est égale à
est égale à 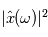 , où
, où 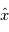 est la transformée de Fourier de
est la transformée de Fourier de 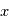 . Si maintenant
. Si maintenant 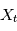 est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de
est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de 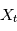 .
.
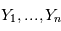 sont des variables aléatoires et
sont des variables aléatoires et 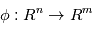 une fonction mesurable alors
une fonction mesurable alors 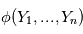 est une variable aléatoire. En particulier, si
est une variable aléatoire. En particulier, si 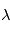 est un scalaire,
est un scalaire, 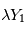 et
et 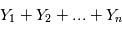 sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
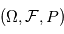 un espace de probabilités, on dit que la suite de variables aléatoires
un espace de probabilités, on dit que la suite de variables aléatoires 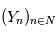 telle que
telle que 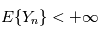 , définies sur cet espace converge en moyenne quadratique si et seulement si:
, définies sur cet espace converge en moyenne quadratique si et seulement si:
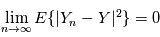
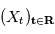 un processus stochastique continu (
un processus stochastique continu (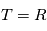 ) tel que chacune des variables aléatoires
) tel que chacune des variables aléatoires 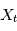 a une espérance finie (
a une espérance finie (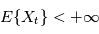 ). L'intégrale en moyenne quadratique du processus
). L'intégrale en moyenne quadratique du processus 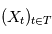 sur l'intervalle
sur l'intervalle ![[a,b]](../pages_ind-vr/equations_etoile/equation44.png) est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
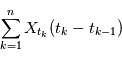
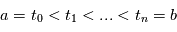 et
et 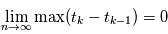 . On la note alors
. On la note alors 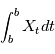 .
.
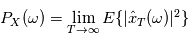
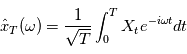
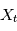 est telle que
est telle que 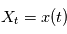 avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors
avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors 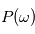 est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle
est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle 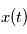 . Dans le cas où les
. Dans le cas où les 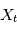 sont aléatoire,
sont aléatoire, 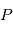 est le carré de la transformée de Fourier "en moyenne" des réalisations de
est le carré de la transformée de Fourier "en moyenne" des réalisations de 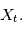 Par exemple si
Par exemple si 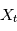 modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant
modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant 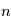 profils de tension
profils de tension 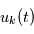 à l'expérience
à l'expérience 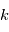 (des réalisations du processus stochastique
(des réalisations du processus stochastique 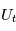 ), la moyenne des carrés du module des transformées de Fourier des
), la moyenne des carrés du module des transformées de Fourier des 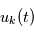 notée
notée 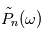 sera approximativement égal à
sera approximativement égal à 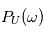 . Si le nombre d'expérience
. Si le nombre d'expérience 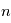 tend vers l'infini
tend vers l'infini 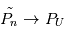 en norme 2.
en norme 2.
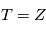 ), on peut directement définir
), on peut directement définir 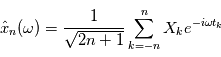 et
et 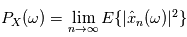 .
.
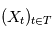 vérifié:
vérifié:
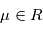 tel que
tel que 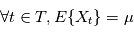
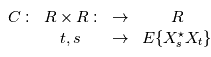 ne dépend que de
ne dépend que de 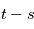 , i. e.
, i. e. 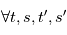 tels que
tels que 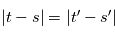 , on a
, on a 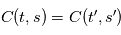 . On note appelle alors habituellement la fonction d'autocorrélation
. On note appelle alors habituellement la fonction d'autocorrélation 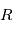 , telle que
, telle que 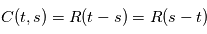
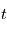 de manière absolue, mais de manière relative à un autre instant. Dans ce cas, la densité spectrale de puissance est égale au carré du module de la transformée de Fourier de la fonction
de manière absolue, mais de manière relative à un autre instant. Dans ce cas, la densité spectrale de puissance est égale au carré du module de la transformée de Fourier de la fonction 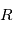 . L'équivalence avec la définition de la densité spectrale de puissance donnée plus haut est établie par le théorème de Wiener-Khinchin.
. L'équivalence avec la définition de la densité spectrale de puissance donnée plus haut est établie par le théorème de Wiener-Khinchin.
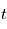 la valeur passe de 1 à -1, la densité de probabilité pour que la valeur passe à 1 à
la valeur passe de 1 à -1, la densité de probabilité pour que la valeur passe à 1 à 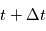 est
est 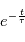 où
où 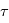 est un réel positif. Pour les vitesses radiales, la densité spectrale de puissance de ces bruits peut être modélisée par::
est un réel positif. Pour les vitesses radiales, la densité spectrale de puissance de ces bruits peut être modélisée par::
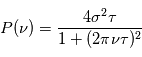
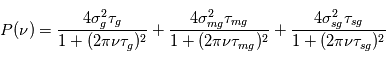
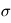 et
et 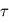 sont ajustés sur le spectre de puissance du signal.
sont ajustés sur le spectre de puissance du signal.
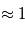 mois), et à plus long terme à travers des cycles d'activité magnétique.
mois), et à plus long terme à travers des cycles d'activité magnétique.
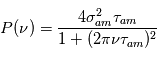

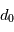 . Vue du dessus, l'atmosphère se comporte approximativement comme un tableau de pixels de taille
. Vue du dessus, l'atmosphère se comporte approximativement comme un tableau de pixels de taille 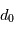 dont chaque cellule introduit une déviation angulaire du faisceau incident. Cette déviation est de l'ordre de
dont chaque cellule introduit une déviation angulaire du faisceau incident. Cette déviation est de l'ordre de 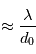 . Dans le cas limite où une cellule a un indice 0 et les cellules avoisinantes ont un indice 1 (sont opaques), on retrouve l'ordre de grandeur de la diffraction. Les fronts d'ondes issus de ces différents pixels arrivent au télescope avec des angles différents, donc donnent chacun une image différente appelé "speckle". L'union de ces speckle forme une tache lumineuse élargie de taille environ égale à
. Dans le cas limite où une cellule a un indice 0 et les cellules avoisinantes ont un indice 1 (sont opaques), on retrouve l'ordre de grandeur de la diffraction. Les fronts d'ondes issus de ces différents pixels arrivent au télescope avec des angles différents, donc donnent chacun une image différente appelé "speckle". L'union de ces speckle forme une tache lumineuse élargie de taille environ égale à 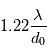 .
.
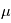 as
Jupiter: 500, 20
as
Jupiter: 500, 20 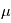 as
à 1 et 10 parsec resp.
as
à 1 et 10 parsec resp.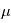 UA
UA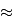 0.5 m/s
à cause des incertitudes sur la rotation de la Terre
et les éphémérides)
0.5 m/s
à cause des incertitudes sur la rotation de la Terre
et les éphémérides)