Problème à deux corps newtonien

Auteur: Nathan Hara & Jacques Laskar

Equation de Newton

Les planètes et l'étoile ont un certain volume. Cependant, on peut montrer que lorsque la distance entre deux corps en intéraction gravitationnelle augmente, leur comportement se rapproche de plus en plus de celui de deux points matériels. On néglige aussi les effets relativistes, de sorte que l'on est ramené à la modélisation de l'intéraction de deux points matériels, dont la résolution va suivre. 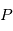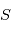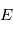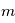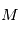Considérons deux points matériels (planète) et (pour "star" de sorte à éviter un conflit de notation avec l'anomalie excentrique ) de masses respectives et et 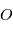l'origine d'un repère Galiléen. Le principe fondamental de la dynamique s'écrit: 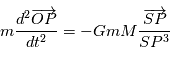$m \frac{d^2\overrightarrow{OP}}{dt^2} = -GmM \frac{\overrightarrow{S P}}{S P^3}$ où 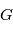est la constante universelle de gravitation.. 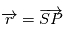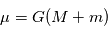En posant $\overrightarrow{r} = \overrightarrow{SP}$ et $\mu = G(M+m)$ on obtient:

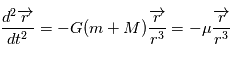
$\frac{d^2 \overrightarrow{r}}{dt^2} = -G(m+M) \frac{ \overrightarrow{r}}{r^3} = -\mu \frac{\overrightarrow{r}}{r^3}$

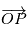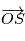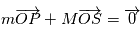On va montrer que la solution de cette équation décrit une conique plane, une ellipse dans le cas des planètes liées à une étoile. On suppose que le système est isolé, on peut donc choisir comme origine du repère le barycentre du système, ce qui permet d'obtenir facilement $\overrightarrow{OP}$ et $\overrightarrow{OS}$ par la relation $m\overrightarrow{OP} + M\overrightarrow{OS} = \overrightarrow{0}$ .

On suppose que le système est isolé, donc le mouvement du barycentre du système {Etoile+planètes} est rectiligne uniforme dans un référentiel galiléen (par exemple le référentiel barycentrique du système solaire).

Quantités conservées

L'équation de Newton est une équation différentielle de degré deux sur des vecteurs de 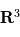$\mathbf{R}^3$ . Pour la résoudre il faut trouver six quantités conservées au cours du mouvement (ou intégrales premières du mouvement) indépendantes. En l'occurrence on peut facilement montrer que deux vecteurs sont conservés au cours du mouvement (ce qui fait deux fois trois composantes, on a bien six scalaires conservés). 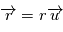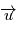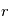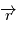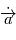Notons $\overrightarrow{r}} = r \overrightarrow{u}$ , où $\overrightarrow{u}$ est un vecteur unitaire (et donc est la norme de $\overrightarrow{r}$ ) et $\dot{\overrightarrow{a}}$ la dérivée par rapport au temps d'un vecteur 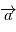$\overrightarrow{a}$ . 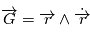On a la conservation du moment cinétique par unité de masse $\overrightarrow{G} = \overrightarrow{r} \wedge \dot{\overrightarrow{r}}$ et du vecteur excentricité 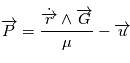$\overrightarrow{P} = \frac{ \dot{\overrightarrow{r}} \wedge \overrightarrow{G} }{\mu} - \overrightarrow{u}$ au cours du mouvement c'est à dire leur dérivée temporelle est nulle

En effet, soit 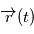$\overrightarrow{r}(t)$ une solution de l'équation de Newton. Alors 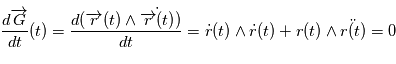$\frac{d \overrightarrow{G}}{dt}(t) = \frac{d( \overrightarrow{r}(t) \wedge \dot{\overrightarrow{r}(t)})}{dt} = \dot{\overightarrow{r}}(t) \wedge \dot{\overightarrow{r}}(t) + \overightarrow{r}(t) \wedge \ddot{\overightarrow{r}(t)} =0$ car d'après l'équation de Newton, 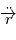$\ddot{\overrightarrow{r}$ est colinéaire à 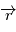$\overrightarrow{r}$ . 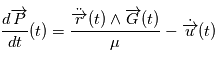D'autre part, $\frac{d\overrightarrow{P}}{dt}(t) = \frac{\ddot{\overrightarrow{r}}(t) \wedge \overrightarrow{G}(t) }{\mu} - \dot{\overrightarrow{u}}(t)$ , or

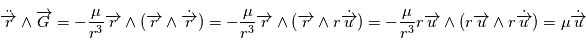
$\ddot{\overrightarrow{r}} \wedge \overrightarrow{G} = - \frac{\mu}{r^3} \overrightarrow{r} \wedge (\overrightarrow{r} \wedge \dot{\overrightarrow{r}}) = - \frac{\mu}{r^3} \overrightarrow{r} \wedge (\overrightarrow{r} \wedge r \dot{\overrightarrow{u}}) = - \frac{\mu}{r^3} r \overrightarrow{u} \wedge (r \overrightarrow{u} \wedge r \dot{\overrightarrow{u}}) = \mu \dot{\overrightarrow{u}}$

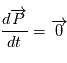Donc $\frac{d\overrightarrow{P}}{dt} = \overrightarrow{0}$ .