Accélération de perspective et changement de parallaxe (astrométrie)

Changement de coordonnées

Définition de $\theta$

Accélération de perspective

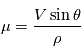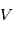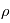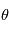L'accélération de perspective est un effet purement géométrique, qui tient à la définition du mouvement propre d'une étoile. Le mouvement propre est en effet défini comme $\mu = \frac{V\sin \theta}{\rho}$ où est la vitesse du système observé, $\rho$ la distance entre l'observateur et le système, $\theta$ est l'angle entre la ligne de visée et la vitesse du système observé. Nous supposons que les mesures astrométriques sont sur un plan. 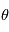Cependant, on mesure la projection du mouvement sur une sphère, donc $\theta$ n'est pas constant au cours du temps. En dérivant par rapport au temps, comme 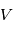est constant:

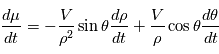
$\frac{d \mu }{dt} = - \frac{V}{\rho^2} \sin \theta \frac{d\rho}{dt}+\frac{V}{\rho} \cos \theta \frac{d\theta}{dt}$

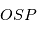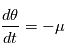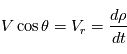On voit sur le triangle OSP que $\frac{d\theta}{dt} = - \mu$ et $V \cos\theta =V_r=\frac{d\rho}{dt}$ . D'où:

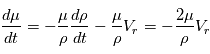
$\frac{d\mu}{dt} = - \frac{\mu}{\rho} \frac{d\rho}{dt} - \frac{\mu}{\rho} V_r = -\frac{2\mu}{\rho} V_r$

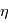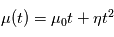En pratique on ajuste un terme quadratique $\eta$ , où le mouvement angulaire sur la sphère céleste est donné par $\mu (t) = \mu_0 t + \eta t^2$ .

Variation de parallaxe

La variation de parallaxe vaut: 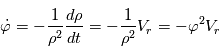$\dot{\varphi}= -\frac{1}{\rho^2} \frac{d\rho}{dt} = -\frac{1}{\rho^2} V_r= - \varphi^2 V_r$ . Comme elle est du deuxième ordre en 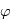$\varphi$ , elle n'est en général pas prise en compte.