Perturbations atmosphériques

Vitesses radiales

L'atmosphère peut influencer la mesure de vitesses radiales de deux manières:

Par atténuation de l'intensité, ce qui augmente le bruit de photon
Par la modification du contenu spectral du signal

La présence de lignes spectrales d'émission ou d'absorption est difficile à corriger. C'est pourquoi on ne considère que des plages de fréquences où l'intensité des raies atmosphériques est inférieure à 1/10000 de l'intensité de la cible. De plus, la réponse de l'atmosphère dépend de la longueur d'onde. Le spectre obtenu est pondéré de sorte à corriger ces inhomogénéités.

Astrométrie

Avant de parvenir au télescope, la lumière issue de l'étoile traverse l'atmosphère. Les turbulences aux hautes altitudes créent des inhomogénéités de densité, donc d'indice optique, qui distordent le front d'onde de la lumière pénétrant dans l'atmosphère. La modélisation classique de ce phénomène passe par l'introduction de "Structure functions" qui modélisent la densité de probabilité des champs de vitesses, densité etc.

Afin de ne pas surcharger le cours, nous ne donnerons qu'un modèle très simple de ce phénomène. Les mouvements de turbulence forment des "cellules" de composition homogène et d'une taille typique 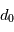d_0 . Vue du dessus, l'atmosphère se comporte approximativement comme un tableau de pixels de taille 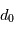d_0 dont chaque cellule introduit une déviation angulaire du faisceau incident. Cette déviation est de l'ordre de 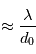$\approx \frac{\lambda}{d_0}$ . Dans le cas limite où une cellule a un indice 0 et les cellules avoisinantes ont un indice 1 (sont opaques), on retrouve l'ordre de grandeur de la diffraction. Les fronts d'ondes issus de ces différents pixels arrivent au télescope avec des angles différents, donc donnent chacun une image différente appelé "speckle". 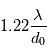L'union de ces speckle forme une tache lumineuse élargie de taille environ égale à $1.22\frac{\lambda}{d_0}$ .