| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Trajectoire observée depuis le barycentre du système solaire |
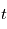 .
.
Le modèle précédent donne le mouvement de l'étoile observée dans un référentiel galiléen, en particulier le référentiel barycentrique du système solaire 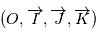 , que l'on munit d'un repère de coordonnées sphériques
, que l'on munit d'un repère de coordonnées sphériques 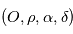 repérant l'étoile
repérant l'étoile 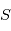 . Supposons que l'observateur est situé en
. Supposons que l'observateur est situé en 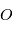 . A un instant
. A un instant 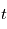 il mesure:
il mesure:
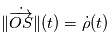
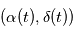 dans le cas de mesures astrométriques
dans le cas de mesures astrométriques
On peut facilement montrer avec un développement limité qu'au premier ordre en 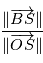 ,
, 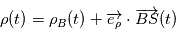 ,
, 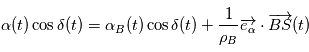 , de même
, de même 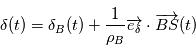 (à faire en exercice).
Supposons que
(à faire en exercice).
Supposons que 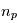 planètes indéxées par
planètes indéxées par 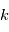 gravitent autour de l'étoile en
gravitent autour de l'étoile en 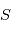 et
et 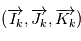 le repère orbital de la planète
le repère orbital de la planète 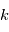 . On projette le mouvement
. On projette le mouvement 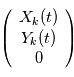 dans le repère orthonormé direct
dans le repère orthonormé direct 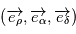 associé aux coordonnées sphériques
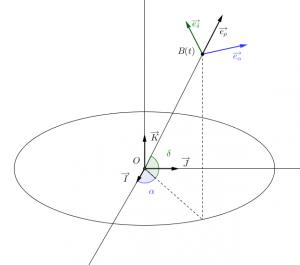
associé aux coordonnées sphériques 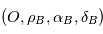 (voir figure). Avec les notations de la page Changement de référentiel:
(voir figure). Avec les notations de la page Changement de référentiel: