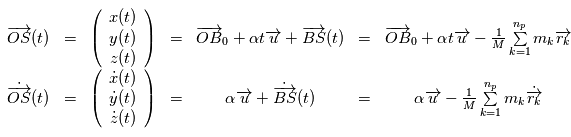Modèle de la trajectoire

Les expressions établies jusqu'ici permettent de paramétrer le mouvement d'une étoile autour de laquelle une planète orbite, en faisant l'hypothèse que les deux corps sont ponctuels, forment un système isolé. Nous allons utiliser ces expressions pour donner un modèle général, lorsque 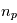n_p planètes orbitent autour de l'étoile.

En notant 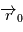$\overrightarrow{r}_0$ et 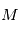respectivement la position et la masse de l'étoile et 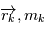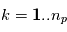$\overrightarrow{r_k}, m_k$ , $k = \mathbf{1}..n_p$ les positions et masses des 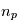n_p planètes , les équations de la mécanique (classique) dans le référentiel barycentrique de ce système sont:

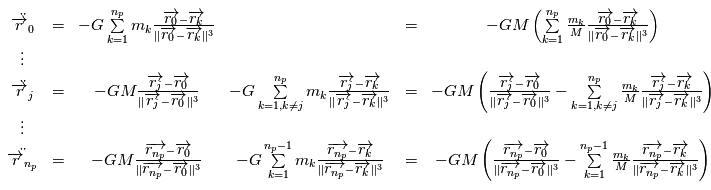
$\begin{array}{cccccc} \ddot{\overrightarrow{r}_0} & = &-G\sum\limits_{k=1}^{n_p} m_k \frac{\overrightarrow{r_0}-\overrightarrow{r_k}}{\|\overrightarrow{r_0}-\overrightarrow{r_k}\|^3} & &=& -GM\left(\sum\limits_{k=1}^{n_p} \frac{m_k}{M} \frac{\overrightarrow{r_0}-\overrightarrow{r_k}}{\|\overrightarrow{r_0}-\overrightarrow{r_k}\|^3 \right) \\ \vdots & & & & & \\ \ddot{\overrightarrow{r}_j} & = &-GM\frac{\overrightarrow{r_j}-\overrightarrow{r_0}}{\|\overrightarrow{r_j}-\overrightarrow{r_0}\|^3}& -G\sum\limits_{k=1, k\not=j}^{n_p} m_k \frac{\overrightarrow{r_j}-\overrightarrow{r_k}}{\|\overrightarrow{r_j}-\overrightarrow{r_k}\|^3}& = &-GM \left(\frac{\overrightarrow{r_j}-\overrightarrow{r_0}}{\|\overrightarrow{r_j}-\overrightarrow{r_0}\|^3} - \sum\limits_{k=1,k\not=j}^{n_p} \frac{m_k}{M} \frac{\overrightarrow{r_j}-\overrightarrow{r_k}}{\|\overrightarrow{r_j}-\overrightarrow{r_k}\|^3} \right) \\ \vdots & & & & & \\ \ddot{\overrightarrow{r}_{n_p}} & = &-GM\frac{\overrightarrow{r_{n_p}}-\overrightarrow{r_0}}{\|\overrightarrow{r_{n_p}}-\overrightarrow{r_0}\|^3}& -G\sum\limits_{k=1}^{n_p-1} m_k \frac{\overrightarrow{r_{n_p}}-\overrightarrow{r_k}}{\|\overrightarrow{r_{n_p}}-\overrightarrow{r_k}\|^3} &=& -GM \left(\frac{\overrightarrow{r_{n_p}}-\overrightarrow{r_0}}{\|\overrightarrow{r_{n_p}}-\overrightarrow{r_0}\|^3} - \sum\limits_{k=1}^{n_p-1} \frac{m_k}{M} \frac{\overrightarrow{r_{n_p}}-\overrightarrow{r_k}}{\|\overrightarrow{r_{n_p}}-\overrightarrow{r_k}\|^3} \right) \end{array}$

En négligeant tous les termes du type 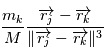$\frac{m_k}{M} \frac{\overrightarrow{r_j} - \overrightarrow{r_k}}{\|\overrightarrow{r_j} - \overrightarrow{r_k} \|^3}$ , c'est à dire l'intéraction entre les planètes, on obtient:

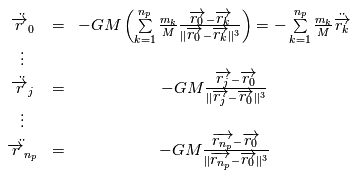
$\begin{array}{cccc} \ddot{\overrightarrow{r}_0} & =& -GM\left(\sum\limits_{k=1}^{n_p} \frac{m_k}{M} \frac{\overrightarrow{r_0}-\overrightarrow{r_k}}{\|\overrightarrow{r_0}-\overrightarrow{r_k}\|^3 \right) = -\sum\limits_{k=1}^{n_p} \frac{m_k}{M} \ddot{\overrightarrow{r_k}} \\ \vdots & & & \\ \ddot{\overrightarrow{r}_j} & = &-GM\frac{\overrightarrow{r_j}-\overrightarrow{r_0}}{\|\overrightarrow{r_j}-\overrightarrow{r_0}\|^3}& \\ \vdots & & & \\ \ddot{\overrightarrow{r}_{n_p}} & = &-GM\frac{\overrightarrow{r_{n_p}}-\overrightarrow{r_0}}{\|\overrightarrow{r_{n_p}}-\overrightarrow{r_0}\|^3}& \end{array}$

En résolvant les 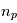n_p problèmes à deux corps associés à chacune des planètes, par 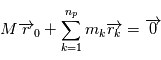$M \overrightarrow{r}_0 + \sum\limits_{k=1}^{n_p} m_k \overrightarrow{r_k} = \overrightarrow{0}$ (dont la première équation du système ci-dessus est la dérivée seconde) on obtient le mouvement de l'étoile. Le modèle de trajectoire complet dans un référentiel galiléen est:

$\begin{array}{ccccccc}\overrightarrow{OS}(t) &=& \left( \begin{array}{c} x(t) \\ y(t) \\ z(t) \end{array}\right) &=& \overrightarrow{OB}_0 + \alpha t \overrightarrow{u} + \overrightarrow{BS}(t) & =& \overrightarrow{OB}_0 + \alpha t \overrightarrow{u} - \frac{1}{M}\sum\limits_{k=1}^{n_p} m_k \overrightarrow{r_k} \\ \dot{\overrightarrow{OS}}(t) &= &\left( \begin{array}{c} \dot{x}(t) \\ \dot{y}(t) \\ \dot{z} (t) \end{array}\right) &=& \alpha \overrightarrow{u} + \dot{\overrightarrow{BS}}(t)&=& \alpha \overrightarrow{u} - \frac{1}{M}\sum\limits_{k=1}^{n_p} m_k \dot{\overrightarrow{r_k}} \end{array}$