| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Trajectoire observée depuis la Terre |
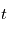 .
.
Le modèle précédent donne l'évolution de l'étoile dans le repère barycentrique du système solaire (RBSS). Or les observations sont disponibles depuis la Terre. Si 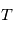 est la position de l'observateur,
est la position de l'observateur, 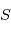 l'étoile cible on a
l'étoile cible on a 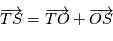
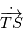 , il faut donc soustraire des observations
, il faut donc soustraire des observations 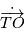
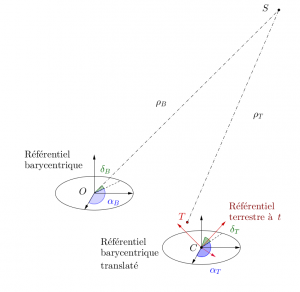
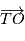 comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure.
comme dans le cas des vitesses radiales, mais aussi s'assurer que toutes les observations sont exprimées dans le même référentiel (par exemple le référenciel barycentrique translaté, sur la figure) alors que chaque observation est dans un référentiel dépendant de l'observation (en rouge sur la figure). L'expression des mesures prises à des instants différents selon une même échelle se pose aussi pour les vitesses radiales, mais passe par l'étalonnage de l'instrument de mesure.
La dérivée temporelle des vecteur est toujours définie par rapport à un référentiel. Ici la notation 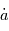 désigne la dérivée temporelle par rapport au RBSS.
désigne la dérivée temporelle par rapport au RBSS.
La détermination de la position du centre de masse de la Terre par rapport au barycentre du système solaire est un sujet à part entière. La trajectoire d'un corps céleste au cours du temps dans un référentiel donné est appelée une éphéméride. Les principaux laboratoires de calcul des éphémérides sont le JPL (NASA) et l'IMCCE (Observatoire de Paris). Les liens envoient sur les générateurs en lignes d'éphémérides respectifs des deux laboratoires. .
La vitesse de l'observateur 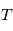 par rapport au barycentre du système solaire peut se décomposer en
par rapport au barycentre du système solaire peut se décomposer en 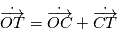 . La partie
. La partie 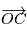 est donné par les éphémérides, comme expliqué plus haut. La correction de la deuxième partie est essentielle: l'observateur parcourt deux fois le rayon terrestre en une nuit, ce qui donne une vitesse d'environ 300 m/s. Si
est donné par les éphémérides, comme expliqué plus haut. La correction de la deuxième partie est essentielle: l'observateur parcourt deux fois le rayon terrestre en une nuit, ce qui donne une vitesse d'environ 300 m/s. Si 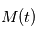 désigne la matrice de changement de repère entre le référentiel lié à la Terre et le référentiel barycentrique du système solaire, on a
désigne la matrice de changement de repère entre le référentiel lié à la Terre et le référentiel barycentrique du système solaire, on a 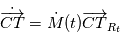 où
où 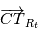 désigne la position de l'observateur dans le référentiel terrestre.
désigne la position de l'observateur dans le référentiel terrestre.
La détermination de 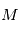 est aussi un sujet à part entière, appelé "rotation de la Terre". Les paramètres de rotations officiels sont donnés par le Service de rotation de la Terre au SYRTE (Observatoire de Paris).
est aussi un sujet à part entière, appelé "rotation de la Terre". Les paramètres de rotations officiels sont donnés par le Service de rotation de la Terre au SYRTE (Observatoire de Paris).
En ce qui concerne l'astrométrie, il faut exprimer la relation entre les positions mesurées et la position dans le RBSS, ce qui peut se décomposer en deux étapes: passer du référentiel terrestre au RBS translaté au centre de masse de la Terre (passer du référentiel rouge au référentiel noir à droite sur la figure), puis passer du référentiel translaté au RBS. Comme on le verra plus tard, il est aussi possible de se passer de cette étape en prenant un champ contenant des étoiles de référence.
Notons 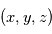 la position de la Terre dans le RBS. En exprimant
la position de la Terre dans le RBS. En exprimant 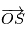 dans le RBSS de deux manières on obtient une relation entre les coordonnées
dans le RBSS de deux manières on obtient une relation entre les coordonnées 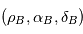 et
et 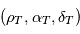 :
:
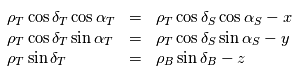
Lorsque 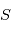 est suffisamment loin, ces expressions différenciées au voisinage de
est suffisamment loin, ces expressions différenciées au voisinage de 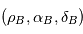 donnent au premier ordre en
donnent au premier ordre en 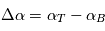 ,
, 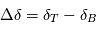 et
et 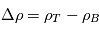
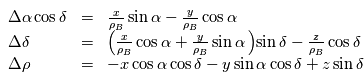
On appelle la quantité 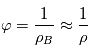 la parallaxe de l'étoile (en général notée
la parallaxe de l'étoile (en général notée 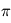 ou
ou 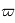 , qui sont des symboles déjà utilisés dans le cours). Elle considérée comme constante au cours des observations et est ajustée aux observations en astrométrie.
, qui sont des symboles déjà utilisés dans le cours). Elle considérée comme constante au cours des observations et est ajustée aux observations en astrométrie.
Remarque: la procédure de changement de référentiel passe par des changements d'échelle de temps (UTC, UT1, TDB...) qui ne seront pas détaillés ici.