En astronomie, lorsqu'une image ou un spectre d'un objet du ciel est obtenu, le résultat varie d'une acquisition à l'autres même si la méthode utilisée est identique: même instrument, même temps de pose, etc. Cela est dû au fait que les photons collectés dans les pixels n'arrivent pas tous de manière uniforme. Si les photons d'une étoile arrivaient à une allure constante de 1 photon par milliseconde sur un pixel, alors un temps de pose de 1 seconde fournirait toujours 1000 photons. Cependant, les photons n'arrivent pas de manière ordonnée, ils suivent une loi dite de Poisson (décrite en détails dans la seconde partie du cours). Cela est dû au fait que les atomes des étoiles créant ces photons agissent de manière chaotique. Par conséquent, si on compte le nombre de photons collectés durant un temps d'une seconde sur 1000 images, on se retrouve avec un échantillon de 1000 valeurs. Il est possible de calculer la moyenne de cet échantillon que l'on note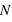 
, qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors 
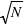; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut 
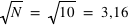. Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
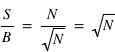
donc 3,16 dans ce cas particulier. Ce rapport s'appelle le rapport Signal sur Bruit, S/B. Dans le cas où le signal N vaut 100 alors le bruit vaut 10 et le signal sur bruit 10. On voit par cet exemple que plus le S/B est grand moins la mesure est entâchée d'erreurs, et vice versa. En astronomie, pour qu'une mesure ait un sens, un S/B d'au moins trois est requis.
