Fonctions de distribution

Pour pallier le problème de la taille des intervalles pour les histogrammes, les statisticiens ont défini la fonction de distribution. Au lieu de calculer le nombre d'occurences dans un intervalle, la fonction de distribution donne le nombre d'occurences inférieures à une valeur. Par souci de comparaison, la fonction de distribution est normalisée, elle est divisée par le nombre total d'éléments de l'échantillon : 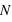. Elle ne peut donc dépasser 1. Dans notre cas, ce nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1 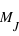, , 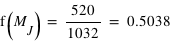ou à une masse terrestre, 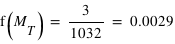. La figure en bas à droite montre cette fonction.

En dessous de la valeur minimale d'un échantillon, cette fonction est nulle. Au delà de la valeur maximale, elle vaut 1. Cette fonction est à créneaux. En passant d'une valeur de l'échantillon à une valeur plus grande elle augmente de la valeur 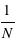du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).

Comme à chaque échantillon correspond une unique fonction de distribution, il est pertinent de comparer deux fonctions de distribution. Cette comparaison indique si deux échantillons ont des propriétés similaires ou différentes. Dans le cas des planètes du système solaire comparé aux exoplanètes, il y a beaucoup de différences. Les masses des planètes du système solaire commencent à 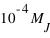alors que celles des exoplanètes à 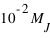, bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17 .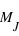