 |  |  |  |  |  |
Techniques et méthodes| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
| | | | | |
Techniques et méthodesExtremum, médiane, quartile |
Dans cette section du cours, nous illustrons les principales valeurs statistiques en utilisant la variable "masse" des exoplanètes.
Les premières valeurs pour caractériser l'échantillon des masses des exoplanètes sont les valeurs minimale et maximale. Elles sont de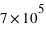 
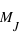et 47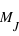 
; la Terre faisant par comparaison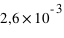 
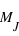. Les masses sont données dans l'unité de la masse de Jupiter, 
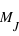, qui fait 
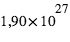kg ou 317,8 masses terrestres . Ce premier critère statistique montre que la masse des planètes découvertes varie sur près de six ordres de grandeur. Cela ne prouve en aucun cas qu'il n'existe pas de planètes plus ou moins massives.
Une autre valeur statistique est la médiane. Cette dernière partage l'échantillon en deux parts égales de telle manière qu'il y a autant de masses inférieures que supérieures à elle. Pour la calculer, il faut tout d'abord trier les masses en ordre croissant. Si le nombre de masses,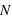 
, est impair la valeur de la
médiane est celle de la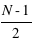 
ème masse. Si le nombre de masse est pair, la médiane se calcule par la moyenne de la 
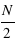et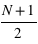 
ème masses. Dans le cas des 1795 exoplanètes découvertes, seules 1032 ont une masse mesurée ; un nombre pair, donc la médiane correspond à la moyenne des masses des exoplanètes numéros 1032/2 = 512 et (1032+1)/2 = 513 qui est la masse 0,96 
.
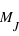Il est aussi possible de connaître la valeur qui marque le premier quart, nommée premier quartile, (0,197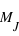 
) ou le dernier quart, nommée dernier quartile (2,75 
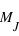) de l'échantillon. Pour un échantillon de taille 
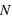, le premier quartile se calcule en prenant la valeur 
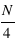, si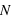 
est un multiple de 4, ou la valeur de l'entier supérieur. Pour le dernier quartile, c'est la même méthode mais en utilisant 
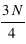. L'écart entre le premier et le dernier quartile est nommé l'écart interquartile.
 |  |