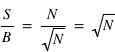Statistique des exoplanètes
Auteur: Sylvain Fouquet
- Introduction
- L'échantillon statistique
- Représentativité d'un échantillon
- Extremum, médiane, quartile
- La boîte à moustaches
- Moyenne et écart-type
- Histogrammes
- Fonctions de distribution
- Statistique multidimensionnelle
- Statistique sur les étoiles hôtes I
- Statistique sur les étoiles hôtes II
- Signal sur Bruit
- Courbe transit
Introduction
Planètes du système solaire
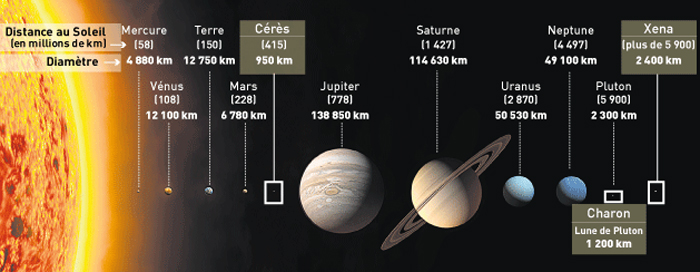
Planètes et planètes naines (encadrées sur fond marron) découvertes dans le système solaire.
Crédit :
http://mash.wifeo.com/astronomie.php
Cette première partie du cours s'intéresse à la statistique à travers le cas particulier des exoplanètes. Cet outil mathématique sert à extraire de l'information de grands échantillons de mesures. Les concepts statistiques décrits ici pour les exoplanètes sont généralisables dans d'autres cas. La statistique découle naturellement de questions scientifiques telles que "combien y a-t-il de planètes dans notre galaxie ?" ou encore "quelles masses ont elles ?" ou "quelles sont leurs distances à leurs étoiles hôtes ?". Ces questions sont déterminantes pour comprendre la formation et l'évolution des planètes et pour aider à la recherche d'une vie extraterrestre.
Avant les années 90, la connaissance sur les planètes se limitait aux neuf planètes du système solaire, Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus, Neptune, Pluton. L'étude des exoplanètes n'existait pas faute d'observation. Il semblait cependant probable que d'autres planètes existaient autour d'autres étoiles que le Soleil, la formation d'une planète ne semblant pas un mécanisme requérant des conditions très spécifiques. Bien qu'Aleksander Wolszczan ait découvert des exoplanètes en septembre 1990 avec le radiotélescope Arecibo autour du pulsar PSR B1257+12 (une étoile en fin de vie, très dense avec une rotation très rapide), la science des exoplanètes a réellement débuté en 1995 avec la découverte de "51 Pegasi b" autour d'une étoile de type solaire par Michel Mayor et Didier Queloz. Plus de dix ans après, près de deux milles exoplanètes ont été découvertes et ce chiffre ne cesse de croître.
En plus des planètes du système solaire, des planètes naines ont été découvertes telles que Cérès. Pluton fut rétrogradée de son rang de planète pour devenir une planète naine.
Avec près de 2000 exoplanètes, des études statistiques permettent de découvrir des propriétés statistiques contraignant les modèles de formation et d'évolution des planètes. Le diagramme de Hubble pour les galaxies et le diagramme Hertzsprung-Russell pour les étoiles sont autant d'outils statistiques fondamentaux pour l'étude des galaxies et des étoiles.
Différentes propriétés sont mesurables pour chaque exoplanète : la masse, le rayon, le type spectral de l'étoile hôte, ... Cette première partie du cours utilise ces grandeurs pour caractériser les exoplanètes et en même temps pour introduire des concepts de statistique qui seront repris d'un point de vue probabiliste dans la seconde partie du cours.
L'échantillon statistique
Définition
Les études statistiques portent sur l'étude d'un échantillon de mesures. Cet échantillon est un ensemble de résultats, de nombres, acquis soit par la répétition d'une même expérience soit par la collection d'observations faites sur le même sujet. Par exemple, le résultat de dix lancers d'un dé, ou de dix dés lancers une fois, forme un échantillon de l'expérience "lancer de dé". Je peux faire la même chose avec des pièces ou des cartes. Moins classique, le résultat d'une pêche peut être vu comme un échantillon statistique des poissons se trouvant là où est le pêcheur. De ce dernier ensemble, la taille des poissons, leurs poids, etc, peuvent être étudiés. Un échantillon se caractérise par son nombre d'éléments. Plus un échantillon est grand, plus son étude est riche et précise.
L'échantillon des exoplanètes
Dans l'étude des exoplanètes, il s'agit de regarder un phénomène qui s'est répété : la formation d'exoplanètes. L'échantillon est donc constitué des exoplanètes découvertes. Actuellement l'échantillon d'exoplanètes connues comporte 1951 (au 8 septembre 2015) exoplanètes situées dans 1235 systèmes exoplanétaires. En effet, certains systèmes planétaires ont plusieurs exoplanètes. Les données utilisées dans ce cours sont fournies par la page internet exoplanet.eu/catalog. De cet échantillon d'exoplanètes, il est possible d'extraire différents échantillons, celui de des masses, des rayons, des eccentricités, etc, puis de les étudier.
Représentativité d'un échantillon
En statistique, le premier souci est la représentativité d'un échantillon. Pour bien comprendre la notion de représentativité, les sondages politiques sont pédagogiques. Durant une élection, un sondage doit donner approximativement le pourcentage de votes qu'obtiendra chaque candidat. Pour ce faire, un échantillon, de 1000 français par exemple, est sondé sur leurs futurs votes. Les sondeurs peuvent alors tirer des conclusions sur l'issue probable du résultat en faisant l'hypothèse que les 60 millions de français vont se comporter comme ces 1000 personnes. Dans ce cas, l'échantillon de 1000 personnes est dit représentatif de la totalité des français. L'échantillon peut cependants être biaisé si le sondeur ne sélectionne que des personnes ayant la carte du premier parti de droite ou bien des personnes lisant uniquement la presse dite de gauche. Il faut donc veiller à corriger le biais s'il est bien connu.
L'obtention d'un échantillon représentatif, sans biais, est une chose facile en théorie mais difficile en pratique. En théorie, il suffit de sélectionner un échantillon de manière aléatoire. Pour les élections, il suffit de tirer un certain nombre de français au hasard. Pour les exoplanètes, cette méthode est impossible pour la simple raison que toutes les exoplanètes de notre galaxie ne sont pas encore connues. Il existe en effet plusieurs biais qui font que certaines exoplanètes peuvent être surreprésentées par rapport à d'autres. Par exemple, les planètes très massives avec un grand rayon et très proches de leurs étoiles auront tendance à être plus facilement détectables et donc à être surreprésentées par rapport aux planètes de type terrestre qui sont petites, peu massives et loin de leurs étoiles hôtes. Toute étude statistique doit alors bien identifier ses biais afin de ne pas tirer de fausses conclusions. Un échantillon d'exoplanètes peut être complet jusqu'à une certaine limite de masse, de taille, de distance au soleil mais pas au-delà. Le travail du statisticien est de trouver cette limite pour tirer des conclusions non biaisées.
Extremum, médiane, quartile
Dans cette section du cours, nous illustrons les principales valeurs statistiques en utilisant la variable "masse" des exoplanètes.
La boîte à moustaches
Boîte à moustaches
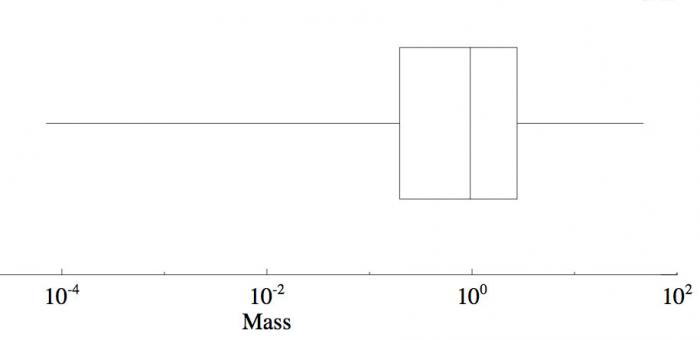
Boîte à moustaches schématisant la distribution des masses des 1032 exoplanètes de l'échantillon. L'axe horizontal représente les masses en échelle logarithmique. Ce schéma résume les cinq valeurs statistiques de la distribution de masse des exoplanètes qui sont par ordre croissant : le minimum (à gauche), le premier quartile (la côté gauche du rectangle), la médiane (le trait au centre du rectangle), le troisième quartile (le côté droit du rectangle) et le maximum (à droite).
Crédit :
Sylvain Fouquet
Boîte à moustaches
Toutes les informations statistiques décrites précédemment peuvent être résumées graphiquement par un schéma appelé la boîte à moustaches. Ce schéma montre les extrema reliés aux quartiles par des segments de droite (les moustaches) et les quartiles reliés à la médiane par des rectangles. La figure ci-dessus illustre une boîte à moustaches dans le cas des masses des exoplanètes. Cette visualisation graphique permet de décrire rapidement comment sont réparties les valeurs. Si les moustaches sont très grandes, cela signifie que les valeurs sont concentrées autour de la médiane. Au contraire, des rectangles de grande taille montrent une distribution dispersée.
Dans le cas de la masse des exoplanètes,cl'écart interquartile, c'est à dire l'écart entre le 1er quartile (0,197 MJ) et le 3ème quartile (2,75 MJ), est de 2,553 MJ.
La dispersion des masses des exoplanètes ne semble pas étendue, mais rappelons que, comme l'échantillon est biaisé vers les grandes masses, ce résultat est sûrement à revoir.
Moyenne et écart-type
Histogrammes
Histogrammes des masses
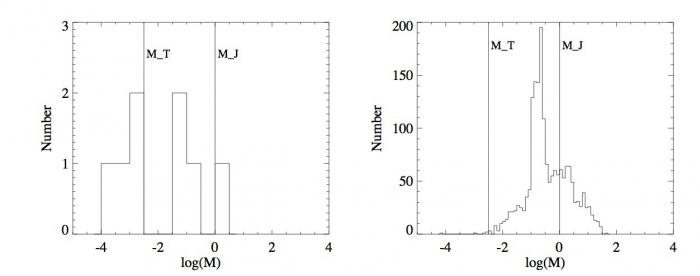
Histogrammes des masses des planètes du système solaire (gauche) et des exoplanètes (droite). L'échelle des masses est en échelle logarithmique par soucis de clarté.
Crédit :
Sylvain Fouquet
Histogramme
Les outils statistiques précédents sont pertinents lorsqu'il s'agit de distributions centrées autour d'une valeur. Dans le cas des planètes du système solaire, les masses sont soit petites (de l'ordre de la masse de la Terre), soit plus massives (de l'ordre de la masse de Jupiter). Cette distribution des masses, en plus d'autres propriétés physiques telles que la taille et la composition chimique, est à la base de la distinction entre les planètes gazeuses et les planètes telluriques.
Calculer la moyenne ou faire une boîte à moustache de l'échantillon des masses des planètes du système solaire ne permet pas de faire la distinction entre planètes telluriques et gazeuses.
Pour avoir une idée plus juste de la répartition des valeurs d'un échantillon, l'histogramme est un outil statistique plus approprié. Il requiert de calculer le nombre d'éléments de l'échantillon inclus dans des intervalles réguliers entre les extrema. L'avantage de l'histogramme est qu'il présente une vision claire de la distribution de notre échantillon. Mais si une taille des intervalles : 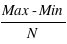 est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
Dans le cas du système solaire, la figure de gauche montre qu'il y a deux pics dans la distribution des masses des planètes autour des masses 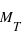 , la masse de la Terre, et
, la masse de la Terre, et 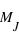 , la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de
, la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de 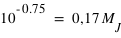 . De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
. De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
Fonctions de distribution
Fonctions de distributions des masses
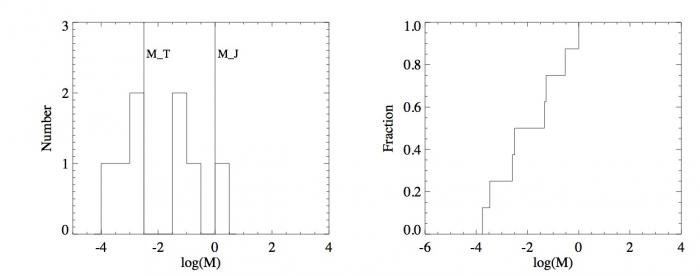
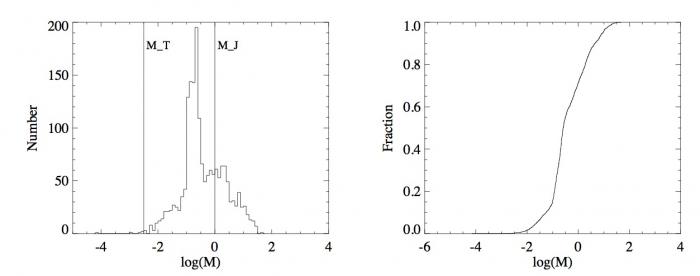
Histogrammes (gauche) et fonctions de distribution (droite) des masses des planètes du système solaire (haut) et des exoplanètes (bas). L'échelle des masses est en échelle logarithmique par soucis de clarté.
Crédit :
Sylvain Fouquet
Pour pallier le problème de la taille des intervalles pour les histogrammes, les statisticiens ont défini la fonction de distribution. Au lieu de calculer le nombre d'occurences dans un intervalle, la fonction de distribution donne le nombre d'occurences inférieures à une valeur. Par souci de comparaison, la fonction de distribution est normalisée, elle est divisée par le nombre total d'éléments de l'échantillon : 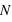 . Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1
. Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1 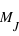 ,
, 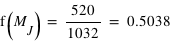 , ou à une masse terrestre,
, ou à une masse terrestre, 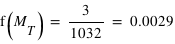 . La figure en bas à droite montre cette fonction.
. La figure en bas à droite montre cette fonction.
En dessous de la valeur minimale d'un échantillon, cette fonction est nulle. Au delà de la valeur maximale, elle vaut 1. Cette fonction est à créneaux. En passant d'une valeur de l'échantillon à une valeur plus grande elle augmente de la valeur 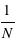 du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
Comme à chaque échantillon correspond une unique fonction de distribution, il est pertinent de comparer deux fonctions de distribution. Cette comparaison indique si deux échantillons ont des propriétés similaires ou différentes. Dans le cas des planètes du système solaire comparé aux exoplanètes, il y a beaucoup de différences. Les masses des planètes du système solaire commencent à 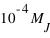 alors que celles des exoplanètes à
alors que celles des exoplanètes à 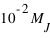 , bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17
, bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17 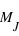 .
.
Statistique multidimensionnelle
Masse, Rayon, demi-grand axe
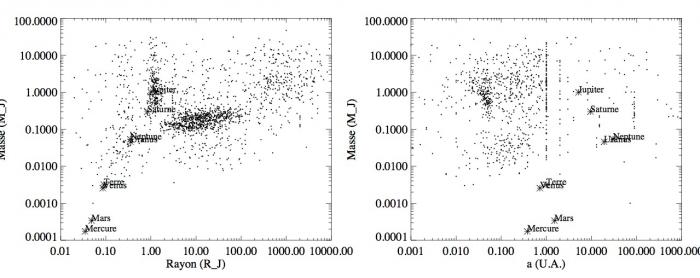
Gauche : Masse des exoplanètes en fonction du rayon (points) avec le cas particulier des planètes du système solaire (étoiles). Droite : demi-grand axe des exoplanètes en fonction de leur masse toujours avec le cas des planètes du système solaire (étoiles).
Crédit :
Sylvain Fouquet
Dans ce cours, la masse des exoplanètes a été étudiée de manière indépendante des autres grandeurs des exoplanètes. Cependant, elle peut être étudiée en parallèle d'autres propriétés. Dans ce type d'étude, des corrélations entre grandeurs sont recherchées. Par exemple, si la densité des exoplanètes, 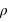 , était constante, ce qui est faux dans notre système solaire, alors le rayon,
, était constante, ce qui est faux dans notre système solaire, alors le rayon, 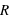 , d'une exoplanète devrait être directement corrélé avec sa masse totale,
, d'une exoplanète devrait être directement corrélé avec sa masse totale, 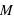 , par la loi
, par la loi 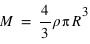 . Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer
. Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer 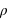 , son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
, son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
En effet, la figure de gauche montre le graphique de la masse des exoplanètes en fonction de leur rayon avec en plus le cas des huit planètes du système solaire. Deux régions plus peuplées ressortent du graphique. La première comporte des planètes de la masse de Jupiter. Dans l'autre région, les exoplanètes ont une masse d'un ordre de grandeur plus petit que Jupiter mais un rayon de 3 à 40 fois supérieur à celui de Jupiter. Les planètes de type Terre, Vénus, Mars ou Mercure sont beaucoup plus rares. Cela est seulement dû aux biais observationnels déjà mentionnés. Ce graphique montre que notre système solaire bien qu'ayant huit planètes ne contient aucune planète du type planète supergéante avec des rayons en moyenne de près de 20 fois le rayon de Jupiter. Il faut aussi se méfier de ces mesures. De telles planètes auraient, et même dépasseraient, la taille du soleil.
La figure de droite illustre le lien entre la distance exoplanète-étoile et la masse des exoplanètes. Là encore, le groupe des masses de Jupiters se distingue. Elles sont très largement aux alentours de 0,05 U.A., bien plus proche que Mercure du Soleil. Ces planètes sont donc des planètes massives collées à leurs étoiles hôtes. Elles sont alors nommées des Jupiter chauds. Encore une fois leur grand nombre apparent est très certainement dû aux observations qui détectent plus facilement ce type de planètes du fait de leurs masses et de la proximité à leurs étoiles hôtes. La grande majorité des autres exoplanètes se situent en dessous d'une U.A. Des ensembles d'exoplanètes forment des traits dans le graphique, par exemple pour la distance de 1 U.A. Cela ne signifie pas qu'il y a de nombreuses planètes se situant à 1 U.A. faisant de cette valeur une valeur exceptionnelle. Cela est sûrement dû à l'algorithme servant à mesurer le demi-grand axe qui favorise cette valeur. Il faut donc se méfier de ces valeurs. Dans ce graphique, davantage que dans le précédent, les planètes du système solaire ne semblent pas en concordance avec celles des exoplanètes. Même Jupiter qui était un cas favorable, se trouve ici avoir des propriétés bien différentes que ses homologues extra-solaires.
Statistique sur les étoiles hôtes I
Relation masse-taille des étoiles hôtes
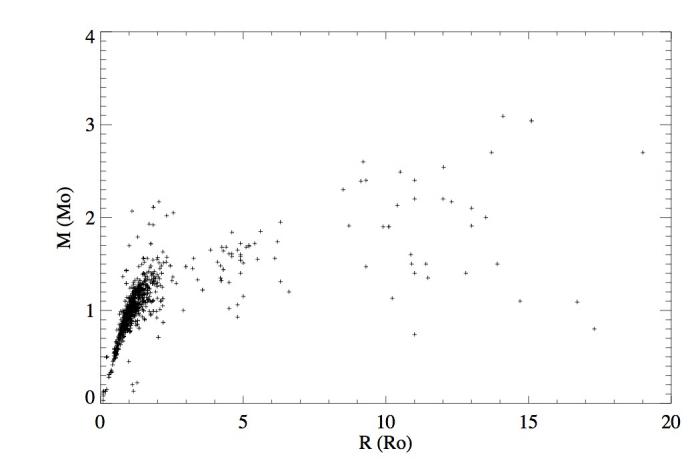
Relation masse-rayon pour les étoiles hôtes des exoplanètes. La distribution montre que les étoiles hôtes ont des propriétés similaires à celles du soleil avec des masses comprises entre 0,5 et 1,5 masse solaire et des rayons compris entre 1 et 2 rayon solaire.
Crédit :
Sylvain Fouquet
Depuis le début de ce cours, seules les propriétés des exoplanètes ont été etudiées. Cependant beaucoup d'informations peuvent être aussi obtenues sur l'étoile hôte autour de laquelle l'exoplanète gravite. En voici les principales : type spectral, masse, rayon, position dans la galaxie ou encore métallicité.
Propriétés des étoiles
Une des premières études statistiques à entreprendre est la caractérisation des étoiles hôtes par leurs masses et leurs tailles. La figure ci-contre montre la relation masse-rayon des étoiles hôtes indiquant que la grande majorité des étoiles ont des masses et des tailles proches de celle du soleil (1 Mo, 1Ro) se situant au centre de la distribution. Cependant, il ne faudrait pas conclure trop hâtivement que seules les étoiles similaires au soleil pourraient abriter des exoplanètes. Notre étoile, le soleil, est une étoile typique parmi les étoiles du disque de la Voie Lactée ; donc lorsque les astrophysiciens cherchent des exoplanètes, ils les cherchent en majorité autour d'étoiles de type solaire. Il y a donc une surreprésentation de ce type stellaire dans l'échantillon des étoiles hôtes. Pour savoir si les exoplanètes peuvent se développer autour d'étoiles ayant des propriétés très différentes de celle du soleil, il faudrait observer un grand nombres d'étoiles de types différents.
L'échantillon actuel des étoiles hôtes ne permet pas une étude poussée pour connaître l'influence de l'environnement d'une étoile hôte sur son nombre d'exoplanètes. Les étoiles proches du soleil, se situant toutes dans le disque plutôt externe de la Voie Lactée, se trouvent dans un milieu peu dense par rapport à des étoiles au centre de la Voie Lactée dans le bulbe. Une étude sur la recherche d'exoplanètes faite dans l'amas globulaire 47 Toucan peut fournir une première indication. La densité de cet amas est bien plus grande que pour les étoiles autour du Soleil. 47 Toucan a de plus des étoiles de faible métallicité, une absence de gaz et des étoiles formées il y près de 12 milliard d'années. Le résultat de cette recherche est de n'avoir trouvé aucune exoplanète alors qu'une même étude faite au voisinage du soleil aurait permis d'en découvrir une vingtaine.
Ce résultat est cohérent avec ce que l'on attend de la formation des planètes. En effet, une étoile pauvre en métaux implique que son environnement est lui-même très probablement pauvre en éléments lourds donc en matériaux pour former une planète. Les amas globulaires sont connus pour être dépourvus de gaz ce qui entraîne l'impossibilité de la formation de planètes gazeuses. De plus un environnement dense n'est pas propice à la formation et à la stabilisation dans le temps d'un disque protoplanétaire autour d'une étoile. Ce disque pourrait avoir tendance à se disperser par interaction gravitationnelle . A l'opposé, il peut être aussi instructif de rechercher des planètes dans des milieux très peu denses comme dans le halo de la Voie Lactée ou dans les galaxies naines proches de la Voie Lactée afin d'être complet.
Statistique sur les étoiles hôtes II
Relation rayon stellaire vs demi-grand axe
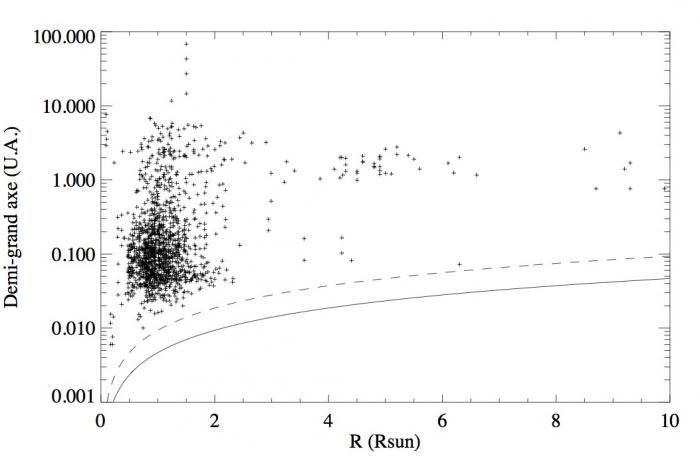
Relation entre le rayon de l'étoile hôte et le demi-grand axe de son exoplanète. La ligne en trait plein montre la limite inférieure pour les demi-grands axes dus à la taille de l'étoile convertie en U.A. La ligne en pointillé montre le double des rayons stellaires.
Crédit :
Sylvain Fouquet
Nombre d'éxoplanètes par étoile
Il est pertinent de savoir si le nombre d'exoplanètes dépend de la masse, de la taille ou du type spectral de l'étoile hôte afin, par exemple, de rechercher des exoplanètes autour d'étoiles qui ont davantage de probabilité d'en abriter. La question "Quelle est la probabilité d'avoir une exoplanète autour d'une étoile" devient alors "Quelle est la probabilité d'avoir une exoplanète autour d'une étoile de type solaire, de type géante rouge de type naine blanche, etc". Cette question permet de se familiariser avec le concept de statistiques conditionnelles ou bayésiennes qui sera développé dans la partie du cours dédié à la théorie des probabilités. La question n'est plus seulement de connaître la probabilité d'avoir un résultat mais sa probabilité à condition qu'un autre évènement ait eu lieu.
Demi-grand axe de l'exoplanète en fontion du rayon de l'étoile
Pour illustrer le concept de statistiques bayésiennes, nous exploitons la figure ci-contre présentant le demi-grand axe des exoplanètes en fonction du rayon de leurs étoiles hôtes. Premièrement, il semble qu'une planète doit être assez éloignée de son étoile hôte durant son orbite sous peine de collision et de destruction. Cela interdit donc des demi-grands axes qui sont d'une taille inférieure à celle du rayon de l'étoile hôte. De plus si une planète a une excentricité forte proche de 1 alors un demi-grand axe élevé n'empêche pas une collision lorsque l'exoplanète passe au péricentre. Dans la figure ci-contre, la ligne en trait plein et celle en tirets montrent le demi-grand axe limite dû à la taille de l'étoile et à son double. Toutes les exoplanètes ont un demi-grand axe en dehors de ces limites ; toutefois, elles sont assez proches de leurs étoiles hôtes. En effet, un demi-grand axe d'une taille de seulement dix fois le rayon de l'étoile hôte est une propriété commune. Au contraire, dans notre système solaire, Mercure est déjà à une distance de plus de 80 fois le rayon du soleil. Cette première discussion implique que plus une étoile a un grand rayon plus la probabilité de trouver une exoplanète de faible demi-grand axe sera faible. En d'autres termes, pour le même demi-grand axe une petite étoile aura plus de chance d'avoir une exoplanète qu'une étoile géante. Cela montre que la probabilité de la valeur du demi-grand axe n'est pas indépendante de la taille de l'étoile hôte, elle est conditionnée.
A l'inverse, pour les étoiles de rayon plus grand que 5 rayons solaires, le demi-grand axe des étoiles semble être statistiquement constant : aux alentours de 2 U.A. Il est évident que ce résultat est faussé par le fait que l'échantillon des étoiles géantes est petit et qu'en plus les étoiles éloignées de plusieurs U.A. sont difficiles à détecter. Cependant, supposons pour la pédagogie, ce résultat vrai. Cela implique que quelque soit la taille d'une étoile hôte entre 5 et 10 rayons solaires, son exoplanète a un demi-grand axe de près de 2 U.A. Dans ce cas, la condition sur la taille de l'étoile hôte n'a aucune influence sur la probabilité du demi-grand axe de l'exoplanète. En statistique, on dira que le demi-grand axe d'une exoplanète est indépendant du rayon de son étoile hôte lorsque ce dernier est entre 5 et 10 rayons solaires.
Signal sur Bruit
En astronomie, lorsqu'une image ou un spectre d'un objet du ciel est obtenu, le résultat varie d'une acquisition à l'autres même si la méthode utilisée est identique: même instrument, même temps de pose, etc. Cela est dû au fait que les photons collectés dans les pixels n'arrivent pas tous de manière uniforme. Si les photons d'une étoile arrivaient à une allure constante de 1 photon par milliseconde sur un pixel, alors un temps de pose de 1 seconde fournirait toujours 1000 photons. Cependant, les photons n'arrivent pas de manière ordonnée, ils suivent une loi dite de Poisson (décrite en détails dans la seconde partie du cours). Cela est dû au fait que les atomes des étoiles créant ces photons agissent de manière chaotique. Par conséquent, si on compte le nombre de photons collectés durant un temps d'une seconde sur 1000 images, on se retrouve avec un échantillon de 1000 valeurs. Il est possible de calculer la moyenne de cet échantillon que l'on note 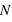 , qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors
, qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors 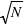 ; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut
; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut 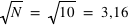 . Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
. Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
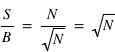
donc 3,16 dans ce cas particulier. Ce rapport s'appelle le rapport Signal sur Bruit, S/B. Dans le cas où le signal N vaut 100 alors le bruit vaut 10 et le signal sur bruit 10. On voit par cet exemple que plus le S/B est grand moins la mesure est entâchée d'erreurs, et vice versa. En astronomie, pour qu'une mesure ait un sens, un S/B d'au moins trois est requis.
Courbe transit
Courbe de transit
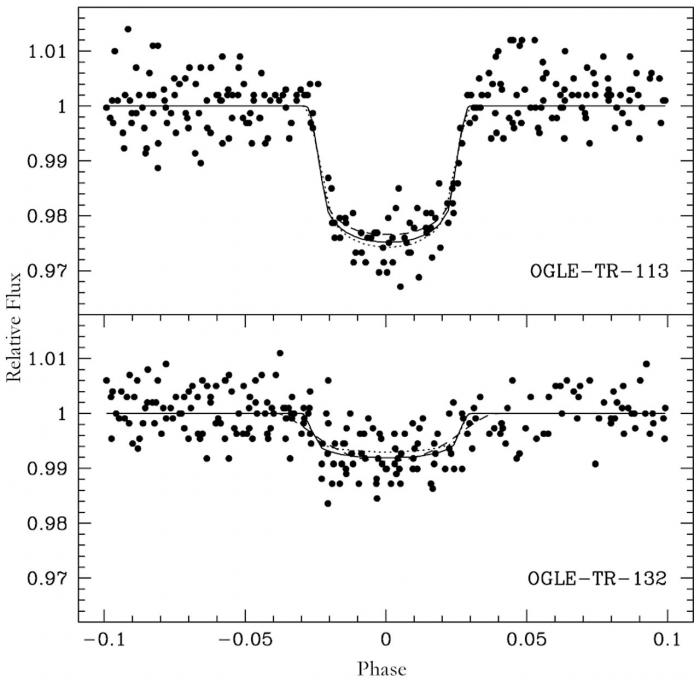
Deux courbes de transit normalisées montrant le passage d'une exoplanète devant son étoile hôte.
Crédit :
ESO
La figure ci-contre illustre, dans le cas plus particulier de la détection des exoplanètes par transit, l'influence du bruit pour détecter une exoplanète. Le graphique supérieur montre un transit assez évident avec une chute puis une remontée de la luminosité . La courbe noire est l'ajustement théorique du flux. Cela représente la courbe sans le bruit, sans la dispersion statistique. Plus réalistes, les points montrent les observations qui sont composées du signal et du bruit. Les courbes sont ici normalisées à 1. Pour le graphique du bas, la décroissance est visible mais plus difficile à modéliser correctement car elle est moins forte. Les deux courbes montrent la présence d'une planète avec des rapports S/B proche de 20. En effet pour un signal de 1 le bruit est de l'ordre de 0,05. Cependant si ce S/B est suffisant pour détecter les deux exoplanètes, il donnera une meilleure précision sur les propriétés (masse, rayon, ...) de l'exoplanète du graphique du haut car le profil de luminosité est plus profond que pour l'exoplanète du graphique du bas.

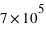
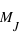 et 47
et 47 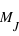 ; la Terre faisant par comparaison
; la Terre faisant par comparaison 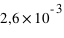
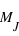 . Les masses sont données dans l'unité de la masse de Jupiter,
. Les masses sont données dans l'unité de la masse de Jupiter, 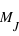 , qui fait
, qui fait 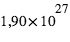 kg ou 317,8 masses terrestres . Ce premier critère statistique montre que la masse des planètes découvertes varie sur près de six ordres de grandeur. Cela ne prouve en aucun cas qu'il n'existe pas de planètes plus ou moins massives.
kg ou 317,8 masses terrestres . Ce premier critère statistique montre que la masse des planètes découvertes varie sur près de six ordres de grandeur. Cela ne prouve en aucun cas qu'il n'existe pas de planètes plus ou moins massives.
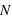 , est impair la valeur de la
médiane est celle de la
, est impair la valeur de la
médiane est celle de la 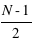 ème masse. Si le nombre de masse est pair, la médiane se calcule par la moyenne de la
ème masse. Si le nombre de masse est pair, la médiane se calcule par la moyenne de la 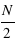 et
et 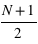 ème masses. Dans le cas des 1795 exoplanètes découvertes, seules 1032 ont une masse mesurée ; un nombre pair, donc la médiane correspond à la moyenne des masses des exoplanètes numéros 1032/2 = 512 et (1032+1)/2 = 513 qui est la masse 0,96
ème masses. Dans le cas des 1795 exoplanètes découvertes, seules 1032 ont une masse mesurée ; un nombre pair, donc la médiane correspond à la moyenne des masses des exoplanètes numéros 1032/2 = 512 et (1032+1)/2 = 513 qui est la masse 0,96 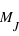 .
.
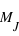 ) ou le dernier quart, nommée dernier quartile (2,75
) ou le dernier quart, nommée dernier quartile (2,75 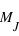 ) de l'échantillon. Pour un échantillon de taille
) de l'échantillon. Pour un échantillon de taille 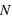 , le premier quartile se calcule en prenant la valeur
, le premier quartile se calcule en prenant la valeur 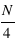 , si
, si 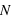 est un multiple de 4, ou la valeur de l'entier supérieur. Pour le dernier quartile, c'est la même méthode mais en utilisant
est un multiple de 4, ou la valeur de l'entier supérieur. Pour le dernier quartile, c'est la même méthode mais en utilisant 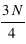 . L'écart entre le premier et le dernier quartile est nommé l'écart interquartile.
. L'écart entre le premier et le dernier quartile est nommé l'écart interquartile.

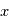 pour un échantillon de taille
pour un échantillon de taille 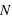 est :
est :
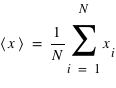
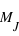 , très proche de la médiane à 2,75
, très proche de la médiane à 2,75 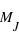 .
.
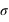 qui se définit par la moyenne des distances à la valeur moyenne. Il faut donc calculer tout d'abord toutes les distances au carré (le carré pour avoir des distances positives), de la moyenne à chaque valeur de l'échantillon,
qui se définit par la moyenne des distances à la valeur moyenne. Il faut donc calculer tout d'abord toutes les distances au carré (le carré pour avoir des distances positives), de la moyenne à chaque valeur de l'échantillon, 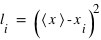 . La moyenne de
. La moyenne de 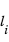 donne le carré de
donne le carré de 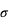 :
:
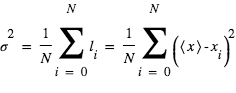
 . Cela est presque deux fois plus grand que l'écart interquartile.
. Cela est presque deux fois plus grand que l'écart interquartile.

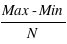 est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
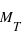 , la masse de la Terre, et
, la masse de la Terre, et 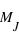 , la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de
, la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de 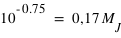 . De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
. De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.


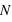 . Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1
. Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1 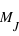 ,
, 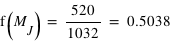 , ou à une masse terrestre,
, ou à une masse terrestre, 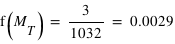 . La figure en bas à droite montre cette fonction.
. La figure en bas à droite montre cette fonction.
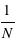 du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
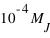 alors que celles des exoplanètes à
alors que celles des exoplanètes à 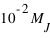 , bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17
, bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17 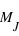 .
.

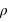 , était constante, ce qui est faux dans notre système solaire, alors le rayon,
, était constante, ce qui est faux dans notre système solaire, alors le rayon, 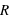 , d'une exoplanète devrait être directement corrélé avec sa masse totale,
, d'une exoplanète devrait être directement corrélé avec sa masse totale, 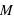 , par la loi
, par la loi 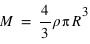 . Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer
. Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer 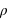 , son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
, son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.


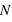 , qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors
, qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors 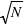 ; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut
; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut 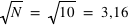 . Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
. Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors