 |  |  |  |  |  |
| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Probabilités conditionnelles |
Faux positifsDifficulté : ☆☆
Lors du dépistage d'une maladie rare, touchant près d'une personne sur mille, les tests ne sont pas fiables à 100%. Après une campagne de dépistage, il y a alors des faux positifs, c'est-à-dire des personnes dépistées comme malades alors qu'elles sont saines. À l'inverse, il y a aussi des faux négatifs, c'est-à-dire des personnes dépistées comme saines mais en réalité malades. Le problème est alors de savoir quelle est la proportion de faux positifs parmi les détections.
On suppose qu'un patient malade est détecté par le dépistage avec une probabilité de 99%. À l'inverse, un patient sain est détecté comme tel avec une probabilité de 95%.
Quel est la malchance d'être diagnostiqué faux-positif, c'est à dire, quelle est la probabilité qu'une personne positive soit en fait non malade ?
Qu'en déduire sur le résultat d'un test positif ? Comment expliquer cela ?
 |  |
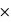P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade) 
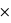P(malade) + P(positif | non malade) 
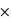P(non malade) = 0,99
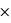0,001 + 0,05
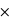0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05 
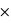0,999 / 0,05094 
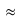0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.