Question 1
Aide :
Pensez à bien énumérer toutes les combinaisons possibles, en se souvenant que l'univers pour l'ensemble des deux dés est donné par le produit cartésien des univers pour chacun des dés.
Solution :
Il y a 6 possibilités d'évènements pour le dé rouge : {1, 2, 3, 4, 5, 6}. Pour chacun de ces évènements, il y en a six autres pour le dé bleu. Donc le nombre total d'évènements est 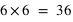 . Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
. Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
Question 2
Aide :
Quels événements de la question précédente sont à présent confondus ? Sur quel critère ? Combien d'événements sont concernés ?
Solution :
Dans ce cas, une méthode lente mais sûre est de lister tous les couples possibles en commençant par tous ceux qui ont le nombre 1 pour le premier dé, puis ceux qui reste avec le 2, ensuite le 3 et ainsi de suite : (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 5), (5, 6), (6, 6). Il est facile de remarquer qu'il y a six couples avec le nombre 1 puis 5 avec le 2 sans réintroduire les couples déjà vus avec le chiffre 1, puis 4, 3, 2, et enfin 1 couple possible avec le chiffre 6 qui est (6,6). Le nombre total de couples est 6+5+4+3+2+1 = 21.
Une autre façon plus rapide de calculer le nombre d'évènements est de repartir du résultat de la question précédente. Sur les 36 couples, seuls les couples avec deux nombres différents peuvent être confondus lorsque les dés sont de la même couleur, par exemple (2, 1) avec (1, 2). Cependant les couples (1, 1), (2, 2), ...(6, 6) ne peuvent pas être confondus avec d'autres. Donc sur les 36 évènements, 30 sont confondables. Chacun de ces 30 cas ne peut être confondu qu'avec un autre couple. (3, 1) n'est confondable qu'avec (1, 3). Sur les 30 évènements, il y en a donc deux fois trop. En résumé, il reste les 6 évènements non confondables et les 15 confondables, on retrouve bien les 21 évènements.
 Cours
Cours Exercice sur les variables aléatoires
Exercice sur les variables aléatoires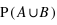 , le signe
, le signe 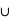 signifiant Union ?
signifiant Union ?
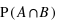 par rapport à
par rapport à 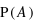 et
et 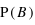 pour des variables discrètes à valeurs dans un ensemble fini ? Donner un exemple où
pour des variables discrètes à valeurs dans un ensemble fini ? Donner un exemple où 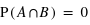 . Notez que le symbole
. Notez que le symbole 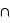 signifie l'intersection.
signifie l'intersection.
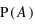 ?
?
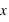 , Démontrer que
, Démontrer que 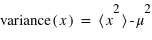 pour une variable discrète. (La démonstration est similaire pour une variable continue en changeant le signe somme en intégrale).
pour une variable discrète. (La démonstration est similaire pour une variable continue en changeant le signe somme en intégrale). 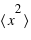 signifie l'espérance de
signifie l'espérance de 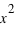 et
et 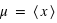 .
.
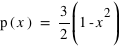 pour x dans l'intervall [0, 1], et
pour x dans l'intervall [0, 1], et 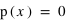 en dehors.
en dehors.
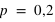 , quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
, quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
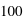 m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre
m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre 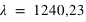 . Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
. Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
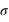 (
(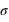 étant l'écart-type) ?
étant l'écart-type) ?
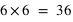 . Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
. Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
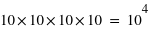 évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
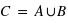 ) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors
) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors 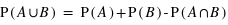 où le symbole
où le symbole 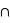 désigne l'intersection.
désigne l'intersection.
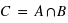 se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble
se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble 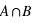 étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles :
étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles : 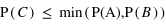 . Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors
. Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors 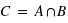 est l'ensemble vide, d'où
est l'ensemble vide, d'où 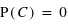 .
.
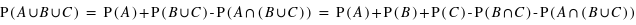 Or
Or 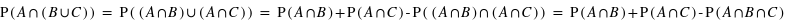 Donc
Donc 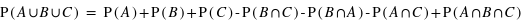
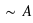 , se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne
, se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne 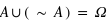 , l'univers des possibles. Or
, l'univers des possibles. Or 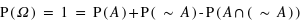 . Comme cette dernière intersection est vide, on a
. Comme cette dernière intersection est vide, on a 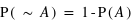 .
.
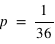
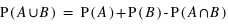 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 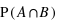 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
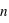 compris entre 2 et 12,
compris entre 2 et 12, 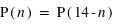 .
.
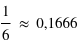 , et celle de faire une somme valant 6 avec deux dés est
, et celle de faire une somme valant 6 avec deux dés est 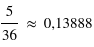 , comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
, comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
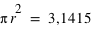 cm2 et celle de la cible tout entière vaut
cm2 et celle de la cible tout entière vaut 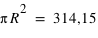 cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible)
cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible) 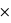 P(toucher la zone centrale | toucher la cible)
P(toucher la zone centrale | toucher la cible) 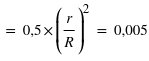 .
.
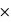 P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade)
P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade) 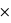 P(malade) + P(positif | non malade)
P(malade) + P(positif | non malade) 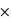 P(non malade) = 0,99
P(non malade) = 0,99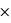 0,001 + 0,05
0,001 + 0,05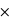 0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05
0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05 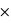 0,999 / 0,05094
0,999 / 0,05094 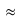 0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
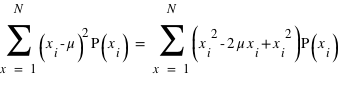 =
= 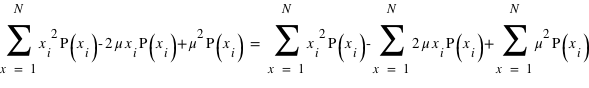 =
= 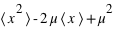 .
Or
.
Or 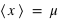 , alors
, alors 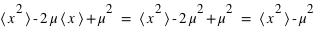 .
Ce qui montre que variance =
.
Ce qui montre que variance = 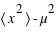 .
.
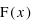 d'une variable aléatoire :
d'une variable aléatoire : 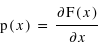 . Cette fonction de distribution décrit la répartition de la variable aléatoire
. Cette fonction de distribution décrit la répartition de la variable aléatoire 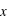 selon l'égalité
selon l'égalité 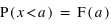
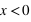 et 1 pour
et 1 pour 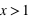 .
La fonction de distribution est l'intégrale de la loi de probabilité. Donc elle vaut
.
La fonction de distribution est l'intégrale de la loi de probabilité. Donc elle vaut 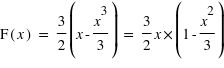 où
où 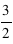 est la constante de normalisation pour que
est la constante de normalisation pour que 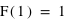 .
.
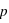 , on a
, on a 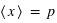 et l'écart-type de
et l'écart-type de 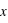 vaut
vaut 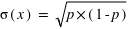
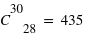 combinaisons pour avoir 28 faces. Il y a
combinaisons pour avoir 28 faces. Il y a 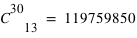 pour avoir 13 piles.
pour avoir 13 piles.
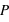 (face) = 0,8,
(face) = 0,8, 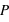 (nombre de "face" = 28) =
(nombre de "face" = 28) = 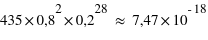 et
et 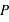 (nombre de "pile" = 13) =
(nombre de "pile" = 13) = 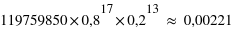
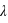 ,
, 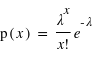 ,
, 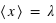 et
et 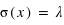
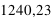 gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
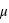 et d'écart-type
et d'écart-type 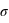 , on a
, on a 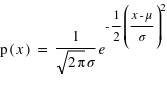
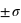 est donnée avec la loi de distribution :
est donnée avec la loi de distribution : 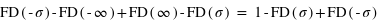 .
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de
.
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de 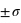 et d'environ 0,0027 en dehors de
et d'environ 0,0027 en dehors de 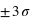 .
.
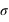 de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10
de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10 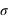 . A trois
. A trois 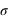 , la probabilité est déjà faible (0,0027) mais à 10
, la probabilité est déjà faible (0,0027) mais à 10 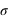 elle est infinitésimale. La théorie semble alors invalidée par l'expérience.
elle est infinitésimale. La théorie semble alors invalidée par l'expérience.