mise à jour : 1 février 2022
mise à jour : 1 février 2022
Probabilités à variables discrètes et équipartition |
Auteur: Sylvain Fouquet
 Lancers de deux dés
Lancers de deux dés
Difficulté : ☆
Question 1)
Soit deux dés distincts que l'on lance, quels sont les différents événements et leurs probabilités ?
AideSolution
On pourra se reporter à l'exercice précédent.
Cette question est déjà vue à la question sur les variables aléatoires. Il y a 36 possibilités qui se définissent par un couple de deux nombres (a, b) où a et b peuvent prendre toutes les valeurs de 1 à 6. Si les dés ne sont pas faussés, chaque événement aura la même probabilité donc 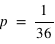
Question 2)
On s'intéresse maintenant à la somme des deux dés. Quels sont les événements possibles et comment sont-ils liés aux événements de la question précédente ? De là, quelles sont leurs probabilités ?
AideSolution
Examiner les valeurs que prend la somme pour chaque événement décrit à la question précédente.
Les événements possibles de sommes sont les nombres de 2 à 12. La preuve en est la liste exhaustive :
- (1, 1) = 2 ; 1 possibilité : Probabilité = 1/36 = 0.02777
- (1, 2) (2, 1) = 3 ; 2 possibilités : Probabilité = 2/36 = 1/18 = 0.05555
- (1, 3) (2, 2) (3, 1) = 4 ; 3 possibilités : Probabilité = 3/36 = 1/12 = 0.08333
- (1, 4) (2, 3) (3, 2) (4, 1) = 5 ; 4 possibilités : Probabilité = 4/36 = 1/9 = 0.11111
- (1, 5) (2, 4) (3, 3) (4, 2) (5, 1) = 6 ; 5 possibilités : Probabilité = 5/36 = 0.1388
- (1, 6) (2, 5) (3, 4) (4, 3) (5, 2) (6, 1) = 7 ; 6 possibilités : Probabilité = 6/36 = 1/6 = 0.16666
- (2, 6) (3, 5) (4, 6) (5, 3) (6, 2) =8 ; 5 possibilités : Probabilité = 5/36 = 0,13888
- (3, 6) (4, 5) (5, 4) (6, 3) = 9 ; 4 possibilités : Probabilité = 4/36 = 0,1111
- (4, 6) (5, 5) (6, 4) = 10 ; 3 possibilités : Probabilité = 3/36 = 0,083333
- (5, 6) (6, 5) = 11 ; 2 possibilités : Probabilité = 2/36 = 0.05555
- (6, 6) = 12 ; 1 possibilités : Probabilité = 1/36 = 0.027777
Cette liste donne les combinaisons pour toutes les sommes de deux dés. En utilisant la loi 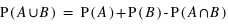 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 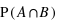 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
Question 3)
Commentez la nouvelle loi de probabilité calculée.
AideSolution
Reconnaît-on une loi du cours ? Donner les différentes caractéristiques observées sur cette loi (symétries éventuelles ?)
Cette loi, de forme "triangulaire", n'est pas équiprobable : la probabilité d'avoir une somme valant 3 n'est pas la même que d'avoir une somme valant 9. Cette loi présente un maximum pour la valeur 7 qui est la valeur la plus probable. Cette loi est symétrique par rapport à 7 car pour tout entier 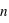 compris entre 2 et 12,
compris entre 2 et 12, 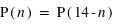 .
.
Question 4)
Vaut-il mieux tenter de faire un 6 avec un dé ou avec la somme de deux dés ?
Solution
La probabilité de faire un 6 avec un dé vaut 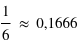 , et celle de faire une somme valant 6 avec deux dés est
, et celle de faire une somme valant 6 avec deux dés est 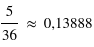 , comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
, comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
 Jeu de fléchettes
Jeu de fléchettes
Difficulté : ☆☆
Question 1)
Soit un jeu de fléchettes avec une cible de rayon 10 cm. Quels événements considère-t-on en général dans ce jeu ? Sur quoi est basée la probabilité de ces derniers ?
AideSolution
Comment compte-t-on les points sur une cible de fléchettes ?
Dans le jeu de fléchettes, les événements sont l'ensemble des positions que peut atteindre la fléchette. Il y a l'extérieur de la cible qui vaut généralement 0 point et des zones à l'intérieur de la cible. Chaque zone de la cible a une surface bien définie. C'est l'étendue de cette surface qui détermine la probabilité de la toucher. Pour un joueur sans aucun talent pour viser, la probabilité de toucher une zone est proportionnelle à sa surface.
Question 2)
On suppose que la moitié des fléchettes n'atteint pas la cible et que la zone centrale donnant le plus de point a un rayon de 1 cm. Quelle est alors la probabilité de faire le maximum de points ?
Solution