Exercice sur la trajectoire circulaire

Auteur: Valérie Ciarletti

Exercice

Difficulté : ☆☆

Vous vous intéressez à la trajectoire du corps fictif 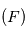(F) de masse 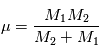$\mu=\frac{M_1M_2}{M_2+M_1}$ qui est en orbite autour du centre de gravité 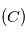(C) du système isolé planète-étoile, ceci dans le cas particulier d'une orbite circulaire.

Question 1)

Utilisez la relation 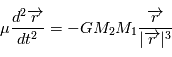$\mu \frac{d^2\overrightarrow{r}}{dt^2}=-G M_2 M_1\frac{\overrightarrow{r}}{|\overrightarrow{r}|^3}$ pour montrer que, dans le cas d'une trajectoire circulaire, la vitesse est constante en module sur toute la trajectoire circulaire suivie par le point fictif 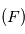(F) autour du centre de masse des deux corps. Exprimez cette vitesse en fonction du rayon 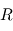du cercle suivi par (F) .

Aide Solution

Question 2)

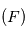Exprimer la période 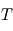de l'orbite (temps mis par le corps pour parcourir une fois le cercle).Vérifier, toujours dans le cas d'une trajectoire circulaire, la deuxième loi de Kepler.

Aide Solution

Question 3)

Dans le cas particulier où ce point est confondu avec le centre de gravité de la planète (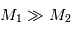 $M_1 \gg M_2$ ), simplifier les expressions obtenues précédemment.

Solution