| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Le problème à deux corps |
On cherche à étudier le mouvement de deux corps de masses 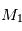 et
et 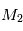 assimilés à deux points matériels localisés aux points
assimilés à deux points matériels localisés aux points 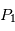 et
et 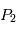 qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel
qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel 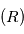 supposé Galiléen d'origine arbitraire.
supposé Galiléen d'origine arbitraire.
Les forces en présence
Lorsque deux corps massiques sont en présence l'un de l'autre, l'effet de la gravitation qui agit sur ces corps se traduit par une force d'attraction. Si ces deux corps sont assimilés à des points matériels localisés en leur centre de gravité, cette force est proportionnelle aux deux masses en jeu et inversement proportionnelle à la distance au carré entre les deux points.
Cette force explique aussi bien la chute des corps sur Terre que le mouvement d'une planète autour de son soleil ou d'une lune autour de sa planète.
On a la force exercée par 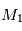 sur
sur 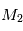 ,
, 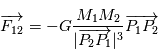 et, par symétrie, la force exercée par
et, par symétrie, la force exercée par 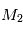 sur
sur 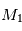 ,
, 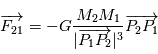
La constante de gravitation universelle est 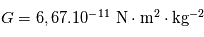
On remarque que 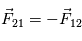 en accord avec la loi de l'action et de la réaction pour un système isolé.
en accord avec la loi de l'action et de la réaction pour un système isolé.
Dans ce référentiel ( ), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
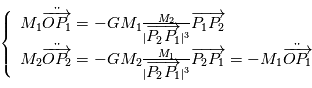
L'objectif est de connaître la position des centres de gravité 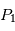 et de
et de 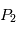 en fonction du temps.
en fonction du temps.
Le choix du référentiel de travail - Réduction à un problème à un corps
Si on considère l'ensemble des deux corps, le centre de gravité (ou barycentre)  est défini de la façon suivante :
est défini de la façon suivante :
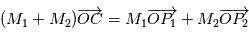
On dérive deux fois par rapport au temps et on utilise le fait que 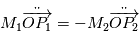 , on obtient alors
, on obtient alors
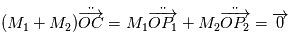
Ce qui traduit le fait que le barycentre  est en mouvement rectligne et uniforme dans le référentiel (
est en mouvement rectligne et uniforme dans le référentiel (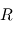 ). Le repère barycentrique (
). Le repère barycentrique (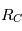 ) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
On choisit de travailler dans le repère (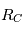 ) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
Les équations du mouvement dans le repère barycentrique (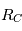 )
)
On note 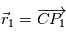 ,
, 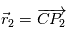
et on introduit 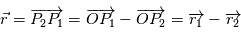
soit 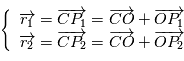
Avec ces notations, les équations du mouvement dans le repère barycentrique deviennent :
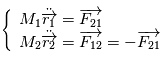
L'expression des forces d'attraction gravitationnelle permet de réécrire ce système sous la forme :
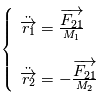 et d'obtenir par différence
et d'obtenir par différence 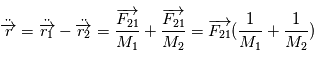
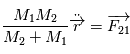
Cette équation peut être interprétée comme l'équation du mouvement d'un corps ponctuel fictif de masse 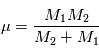 (appeléee masse réduite du système) soumis à la force
(appeléee masse réduite du système) soumis à la force 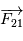 , soit
, soit 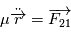 . Dans la suite, ce point fictif sera noté
. Dans la suite, ce point fictif sera noté 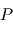 .
.
Le problème à deux corps se réduit donc à un problème à un corps fictif unique. On aboutit à une équation unique pour le mouvement de 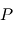 dans laquelle n'apparait que l'inconnue
dans laquelle n'apparait que l'inconnue 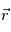 .Cette équation est valable dans le repère baycentrique (
.Cette équation est valable dans le repère baycentrique (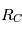 ).
).
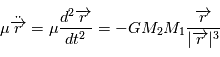
L'expression de la force de gravité permet a priori de modéliser l'interaction entre plusieurs corps (étoiles, planètes, lunes, petits corps ...). Cependant, seul le problème à deux corps peut être mathématiquement résolu sans approximation.