Equation de la trajectoire

Auteur: Valérie Ciarletti

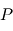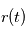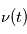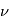Les solutions de l'équation du mouvementpermettent de déterminer la façon dont la position du point déterminée par les deux variables r(t) et $\nu(t)$ évolue au cours du temps. Cependant, la résolution de cette équation différentielle, n'est pas possible analytiquement. Nous allons donc nous focaliser sur la relation entre la distance r et l'angle polaire $\nu$ qui modélise la trajectoire du point 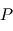dans le plan de l'orbite.

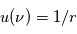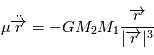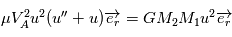
Le résultat recherché est obtenu en utilisant la fonction $u(\nu)=1/r$ introduite précédemment. Avec cette nouvelle variable, l'équation ${\mu}\ddot{\overrightarrow{r}}}=-G M_2 M_1\frac{\overrightarrow{r}}{|\overrightarrow{r}|^3}$ devient ${\mu}V_A^2u^2(u''+u)\overrightarrow{e{_r}}=G M_2 M_1u^2\overrightarrow{e{_r}}$

soit après simplifications : 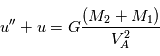$u''+u=G \frac{(M_2+M_1)}{ V_A^2}$

Remarque : Cette équation peut également être obtenue en utilisant la conservation de l'énergie mécanique (cinétique+potentielle) du point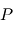

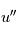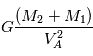L'équation à résoudre est une équation différentielle du second ordre (présence de u'' ) à coefficients constants avec second membre constant $G \frac{(M_2+M_1)}{ V_A^2}$ .

La solution de cette équation est la somme d'une solution particulière de l'équation complète avec second membre et de la solution générale de l'équation sans second membre. On choisit comme solution particulière la solution constante égale à 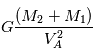$G \frac{(M_2+M_1)}{ V_A^2}$ .

La solution générale de l'équation sans second membre 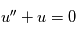u''+u=0 est une fonction sinusoïdale de phase à l'origine et d'amplitude qui dépendent des conditions initiales du problème.

Au final, on obtient donc une solution de la forme 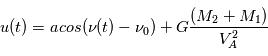$u(t)=a cos(\nu(t)-{\nu}_0)+G \frac{(M_2+M_1)}{ V_A^2}$ .

Il est maintenant possible de repasser à la fonction 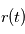r(t) et on obtient l'équation en polaire d'une conique :

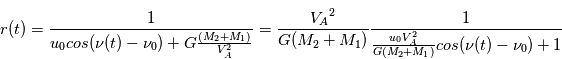
$r(t)=\frac{1}{u_0 cos(\nu(t)-{\nu}_0)+G \frac{(M_2+M_1)}{ V_A^2}}=\frac{ {V_A}^2}{G(M_2+M_1)}\frac{1}{\frac{u_0 V_A^2}{G(M_2+M_1)} cos(\nu(t)-{\nu}_0)+1}$

Par identification aux paramètres de l'équation classique de l'ellipse 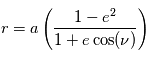$r=a \left( \frac{1-e^2}{1+e \cos(\nu)} \right)$ , on a

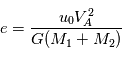$e= \frac{u_0 V_A^2}{G(M_1+M_2)}$ et $a= \frac{\frac{{V_A}^2}{G(M_1+M_2)}}{1-{{(\frac{u_0 V_A^2}{G(M_1+M_2)}})}^2}$