Etude du mouvement

Auteur: Valérie Ciarletti

Démonstration de la loi des aires - Deuxième loi de Kepler

A partir du moment cinétique, il est aussi possible de démontrer la loi des aires.

Nous avons démontré précédemment que la trajectoire du point 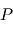restait dans un plan fixe qui est perpendiculaire à la direction du moment cinétique constant. Dans ce plan, il est donc possible de décrire le mouvement en coordonnées polaires. l'angle polaire sera noté ν (il s'agit de l'anomalie vraie définie dans La première loi de Kepler )

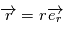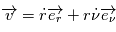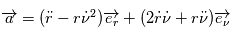
Dans ce système de coordonnées, on a $\overrightarrow{r}=r\overrightarrow{e{_r}}$ , $\overrightarrow{v}=\dot\overright{r}\overrightarrow{e{_r}}+r\dot\overright{\nu}\overrightarrow{e{_\nu}}$ et $\overrightarrow{a}=(\ddot\overright{r}-r\dot\overright{\nu}^2)\overrightarrow{e{_r}}+(2\dot\overright{r}\dot\overright{\nu}+r\ddot{\nu})\overrightarrow{e{_\nu}}$

Il est possible dès à présent de simplifier l'experssion de l'accélération puisque la force n'a pas de composante que selon l'axe 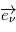$\overrightarrow{e{_\nu}}$ . On a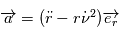 $\overrightarrow{a}=(\ddot\overright{r}-r\dot\overright{\nu}^2)\overrightarrow{e{_r}}$

Avec ces notation, le moment cynétique constant s'écrit 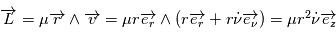${\overrightarrow{L}}=\mu \overrightarrow{r}} \wedge\overrightarrow{v}}=\mu r\overrightarrow{e{_r}}\wedge(\(r\overrightarrow{e{_r}}+r\dot\overright{\nu}\overrightarrow{e{_\nu}})=\mu r^2\dot\overright{\nu}\overrightarrow{e{_z}}$ .

On démontre ainsi, puisque 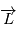${\overrightarrow{L}}$ est un vecteur constant, que la quantité 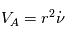$V_A=r^2\dot\overright{\nu}$ (appelée vitesse aréolaire) reste constante lors du mouvement du corps autour du point .

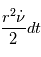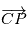Or $\frac{r^2\dot\overright{\nu}}2 dt$ est l'aire balayée pendant la durée dt par le vecteur ${\overrightarrow{CP}}$ .

Géométrie illustrant la loi des aires

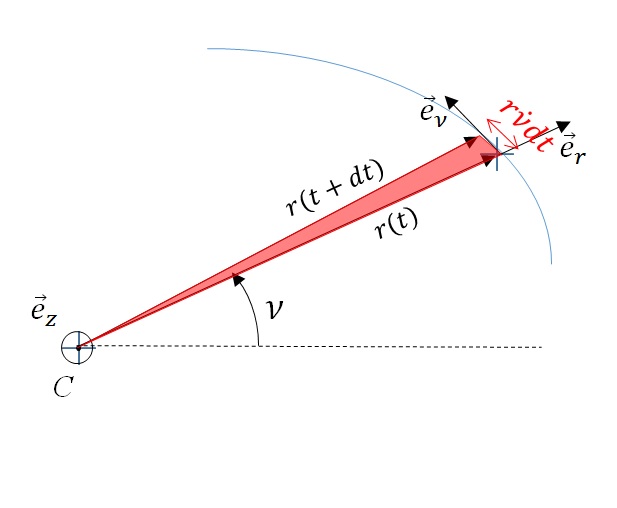
On en déduit donc que la surface balayée (en rouge sur la figure) pendant un temps 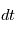donné est constante le long de la trajectoire et égale à 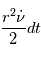$\frac{r^2\dot\overright{\nu}}2 dt$ . C'est la loi des aires de Kepler.

Remarque 1 : On peut également noter que si 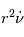$r^2\dot\overright{\nu}$ est une constante, alors le signe de 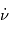$\dot\overright{\nu}$ est constant, ce qui traduit le fait que la rotation s'effectue toujours dans le même sens.

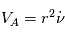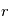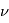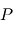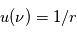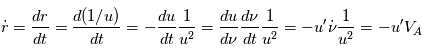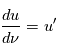
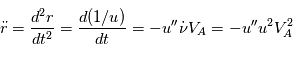Remarque 2 : On peut utiliser la relation $V_A=r^2\dot\overright{\nu}$ pour exprimer les dérivées de et de $\nu$ par rapport au temps et réecrire l'accélération du point en introduisant la fonction $u(\nu)=1/r$ . 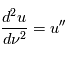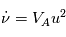$\dot{r}=\frac{dr}{dt}=\frac{d(1/u)}{dt}=-\frac{du}{dt}\frac{1}{u^2}=\frac{du}{d\nu}\frac{d\nu}{dt}\frac{1}{u^2}=-u'\dot{\nu}\frac{1}{u^2}=-u'V_A$ en notant $\frac{du}{d\nu}=u'$ $\ddot{r}=\frac{d^2r}{dt^2}=\frac{d(1/u)}{dt}=-u''\dot{\nu}V_A=-u''u^2V_A^2$ en notant $\frac{d^2u}{d\nu^2}=u''$ $\dot\overright{\nu}=V_Au^2$

L'accélération 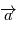$\overrightarrow{a}$ devient alors 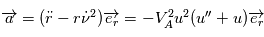$\overrightarrow{a}=(\ddot\overright{r}-r\dot\overright{\nu}^2)\overrightarrow{e{_r}}=-V_A^2u^2(u''+u)\overrightarrow{e{_r}}$ . Cette expression sera utilisée par la suite pour trouver l'équation de la trajectoire du point .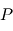