Etude du mouvement

Auteur: Valérie Ciarletti

On part de l'équation obtenue précédemment 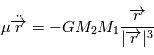${\mu}\ddot{\overrightarrow{r}}}=-G M_2 M_1\frac{\overrightarrow{r}}{|\overrightarrow{r}|^3}$ dans le repère barycentrique ( R_C ).

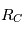Le vecteur position 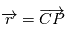$\overrightarrow{r}=\overrightarrow{CP}$ est défini à partir du centre de gravité qui l'origine du repère.

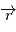$\overrightarrow{r}$ est l'inconnue dont il faut déterminer l'évolution en fonction du temps.

Démonstration de la planeité de la trajectoire - Première loi de Kepler

On démontre en utilisant le théorème du moment cinétique que la trajectoire du point 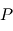est plane. C'est la première loi de Kepler.

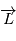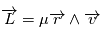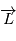Le moment cinétique $\overrightarrow{L}$ d'un point en mouvement est défini, pour un repère particulier et par rapport à l'origine du repère, de la façon suivante ${\overrightarrow{L}}=\mu \overrightarrow{r}} \wedge\overrightarrow{v}}$ . 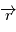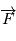Le théorème du moment cinétique (qui se déduit des lois de la mécanique) exprime le fait que la dérivée de ce moment cinétique $\overrightarrow{L}$ est le produit vectoriel du rayon vecteur $\overrightarrow{r}$ et de la force $\overrightarrow{F}$ .

Pour le cas qui nous intéresse, dans le repère barycentrique (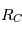 R_C ) au point , on a donc

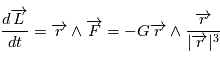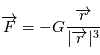
$\frac{d\overrightarrow{L}}{dt}=\overrightarrow{r}} \wedge\overrightarrow{F}}=-G \overrightarrow{r}} \wedge\frac{\overrightarrow{r}}{|\overrightarrow{r}|^3}$ puisque $\overrightarrow{F}=-G \frac{\overrightarrow{r}}{|\overrightarrow{r}|^3}$

Le produit vectoriel de deux vecteurs colinéaires étant nul, on obtient 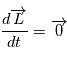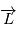$\frac{d\overrightarrow{L}}{dt}=\overrightarrow{0}$ . $\overrightarrow{L}$ est donc un vecteur constant.

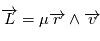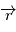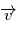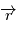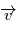Or, du fait du produit vectoriel, le vecteur ${\overrightarrow{L}}=\mu \overrightarrow{r}} \wedge\overrightarrow{v}}$ doit être orthogonal à chacun des vecteurs $\overrightarrow{r}$ et $\overrightarrow{v}$ . On montre ainsi que le plan défini en tout instant par les deux vecteurs $\overrightarrow{r}$ et $\overrightarrow{v}$ est invariant (orthogonal à l'axe défini par ce vecteur constant 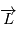$\overrightarrow{L}$ ). C'est le plan dans lequel le point évolue.

En conclusion, la trajectoire du point 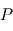est bien plane.