| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Conclusion pour le problème à deux corps |
Dans un référentiel galiléen quelconque de centre 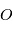 , le mouvement de l'étoile
, le mouvement de l'étoile 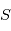 en fonction du temps peut s'écrire:
en fonction du temps peut s'écrire:
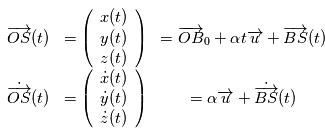
Où 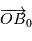 est la position du barycentre
est la position du barycentre 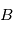 du système {Etoile, Planète} à
du système {Etoile, Planète} à 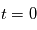 ,
, 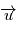 est la direction du mouvement de
est la direction du mouvement de 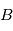 et
et 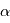 son module.
son module.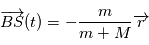 où
où 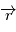 vérifiel'équation de Newton
vérifiel'équation de Newton 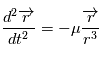 , qui est une équation différentielle de degré deux sur l'espace. Lorsque
, qui est une équation différentielle de degré deux sur l'espace. Lorsque 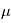 est fixé et la position et la vitesse à
est fixé et la position et la vitesse à 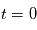 ,
, 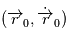 sont connus, la position et la vitesse sont données par le flot:
sont connus, la position et la vitesse sont données par le flot: 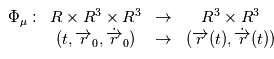 . En d'autres termes, les sept paramètres
. En d'autres termes, les sept paramètres 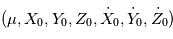 définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple
définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple 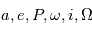 et
et 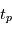 , qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
, qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
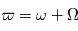 : la longitude du périhélie
: la longitude du périhélie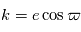
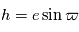
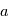 : le demi-grand axe
: le demi-grand axe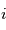 : l'inclinaison
: l'inclinaison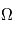 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant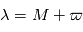 : la longitude
: la longitudeCes éléments sont des fonctions continues de l'inclinaison et de l'excentricité.