Exercices

Auteur: Nathan Hara & Jacques Laskar

Conservation de l'énergie

Difficulté : ☆☆

Question 1)

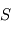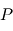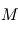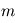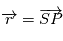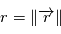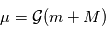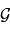Pour établir l'équation du mouvement, les conservations du moment cinétique et du vecteur eccentricité suffisent. On a une autre intégrale du mouvement: l'énergie. Considérons deux points matériels et de masses respectives et . On pose $\overrightarrow{r} = \overrightarrow{SP}$ , $r = \|\overrightarrow{r}\|$ et $\mu = \mathcal{G}(m+M)$ où $\mathcal{G}$ est la constante universelle de gravitation.

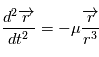
Montrer que $\frac{d^2\overrightarrow{r}}{dt^2} = -\mu \frac{\overrightarrow{r}}{r^3}$
Calculer l'énergie potentielle associée à la force de gravitation
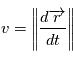On note $v = \left\| \frac{d \overrightarrow{r}}{dt} \right\|$ . Déduire du théorème de l'énergie mécanique que 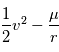$\frac{1}{2} v^2 - \frac{\mu}{r}$ est une quantité constante au cours du mouvement
Quel est le point de l'orbite où la vitesse de l'étoile est la plus élevée ? la moins élevée ?