| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Changement de référentiel |
Les observations sont disponibles dans un référentiel 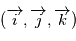 où
où 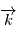 est la direction d'observation et
est la direction d'observation et 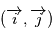 sont choisis de sorte que le repère est orthonormé direct. Le repère
sont choisis de sorte que le repère est orthonormé direct. Le repère 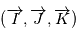 est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
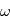 d'axe
d'axe 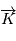 (parallèle au moment cinétique), cet angle est appelé argument du périastre. Le repère obtenu par cette rotation est noté
(parallèle au moment cinétique), cet angle est appelé argument du périastre. Le repère obtenu par cette rotation est noté 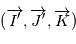 .
. 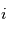 d'axe
d'axe 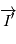 , c'est l' inclinaison
, c'est l' inclinaison 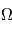 d'axe
d'axe 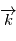 , c'est l'ascension droite au noeud ascendant
, c'est l'ascension droite au noeud ascendant
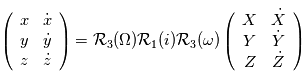
Où:
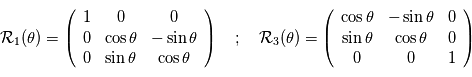
Soit 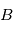 le barycentre du système {planète+étoile}, on note
le barycentre du système {planète+étoile}, on note 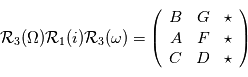 où
où 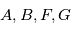 sont appelées les constantes de Thiele-Innes. On conserve la notation classique pour ces constantes, qui sautent quelques lettres de l'alphabet pour une raison inconnue des auteurs. La notation
sont appelées les constantes de Thiele-Innes. On conserve la notation classique pour ces constantes, qui sautent quelques lettres de l'alphabet pour une raison inconnue des auteurs. La notation 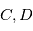 n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que
n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que 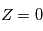 , ils n'apparaissent jamais dans les calculs
, ils n'apparaissent jamais dans les calculs
On peut caractériser l'orbite par les éléments suivants:
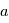 : le demi-grand axe
: le demi-grand axe 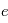 : l'excentricité
: l'excentricité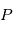 : la période
: la période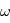 : l'argument du périastre
: l'argument du périastre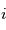 : l'inclinaison
: l'inclinaison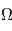 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant
Ces éléments donnent la géométrie de l'orbite. Pour déterminer la position de la planète à un instant 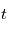 donné, il faut de plus connaître l'instant de son passage au périastre
donné, il faut de plus connaître l'instant de son passage au périastre 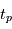 . On peut alors calculer
. On peut alors calculer 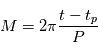 connaisant
connaisant 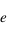 on peut calculer l'anomalie excentrique
on peut calculer l'anomalie excentrique 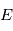 par l'équation de Kepler, puis l'anomalie vraie
par l'équation de Kepler, puis l'anomalie vraie 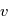 . On en déduit la position sur l'ellipse par l'équation donnée page "Loi des aires",
. On en déduit la position sur l'ellipse par l'équation donnée page "Loi des aires", 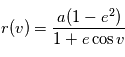 . Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.
. Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.