Géométrie de l'orbite

Auteur: Nathan Hara & Jacques Laskar

Géométrie du mouvement elliptique

Le mouvement est dans le plan $(\overrightarrow{P}, \overrightarrow{Y})$

Les quantités conservées définies page précédente permettent de donner une description géométrique de l'évolution de 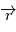$\overrightarrow{r}$ .

On déduit de la conservation du moment cinétique que le mouvement est plan. En effet, 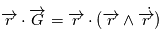$\overrightarrow{r}\cdot\overrightarrow{G} = \overrightarrow{r} \cdot (\overrightarrow{r} \wedge \dot{ \overrightarrow{r}) }$ et comme 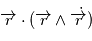$\overrightarrow{r} \cdot (\overrightarrow{r} \wedge \dot{ \overrightarrow{r}) }$ est un produit mixte, il est invariant par permutation circulaire: 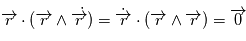$\overrightarrow{r} \cdot (\overrightarrow{r} \wedge \dot{ \overrightarrow{r}) } = \dot{\overrightarrow{r}} \cdot (\overrightarrow{r} \wedge \overrightarrow{r}) } = \overrightarrow{0}$ car le produit vectoriel de deux vecteurs colinéaires est nul. 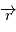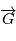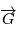Le vecteur $\overrightarrow{r}$ est orthogonal à $\overrightarrow{G}$ à tout instant, autrement dit le mouvement est dans un plan orthogonal à $\overrightarrow{G}$ .

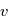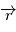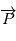Notons l'angle entre $\overrightarrow{r}$ et $\overrightarrow{P}$ et posons 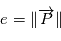$e = \|\overrightarrow{P} \|$ . Alors comme 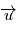$\overrightarrow{u}$ est unitaire, 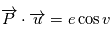$\overrightarrow{P} \cdot \overrightarrow{u} = e \cos v$ d'autre part en remplaçant 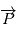$\overrightarrow{P}$ par sa définition, on a 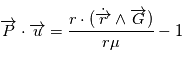$\overrightarrow{P} \cdot \overrightarrow{u} = \frac{\overrightrarrow{r} \cdot ( \dot{\overrightarrow{r}} \wedge \overrightarrow{G} )}{r \mu} -1$ et comme 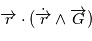$\overrightarrow{r} \cdot ( \dot{\overrightarrow{r}} \wedge \overrightarrow{G} )$ est un produit mixte, 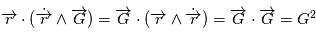$\overrightarrow{r} \cdot ( \dot{\overrightarrow{r}} \wedge \overrightarrow{G} ) = \overrightarrow{G} \cdot ( \overrightarrow{r} \wedge \dot{\overrightarrow{r}} ) = \overrightarrow{G} \cdot \overrightarrow{G} = G^2$ . où 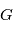est la norme de 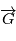$\overrightarrow{G}$ . On obtient alors 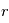en fonction de :

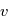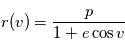
$r(v) = \frac{p}{1+e \cos v}$

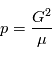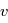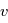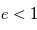Où $p = \frac{G^2}{\mu}$ , qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de , appelée anomalie vraie. Cependant, nous voulons exprimer la solution en fonction du temps, l'objet de la page suivante est d'exhiber une relation entre et le temps. On sait que lorsque e < 1 , il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que 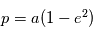p = a(1-e^2) où 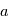est le demi-grand axe de l'ellipse. 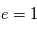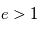Si e = 1 ou e>1 , la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.

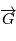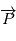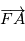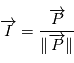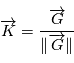L'orbite est dans un plan perpendiculaire à $\overrightarrow{G}$ , et le vecteur $\overrightarrow{P}$ est parallèle à $\overrightarrow{FA}$ . Notons $\overrightarrow{I}= \frac{\overrightarrow{P}}{\|\overrightarrow{P} \|}$ et $\overrightarrow{K}= \frac{\overrightarrow{G}}{\|\overrightarrow{G} \|}$ . On introduit un vecteur 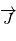$\overrightarrow{J}$ de sorte que 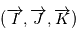$(\overrightarrow{I}, \overrightarrow{J}, \overrightarrow{K})$ forme une base orthonormale.