Loi des aires

Auteur: Nathan Hara & Jacques Laskar

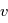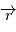Nous avons montré que la solution au problème des deux corps est plane, et peut s'exprimer en fonction de l'anomalie vraie , angle entre le vecteur excentricité et le vecteur $\overrightarrow{r}$ .

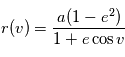
$r(v) = \frac{a(1-e^2)}{1+e \cos v}$

Afin d'exprimer 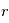en fonction du temps on va introduire successivement deux variables, 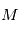et 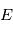appelées respectivement 'anomalie moyenne et 'anomalie excentrique.

Loi des Aires

Avec les notations précédentes, 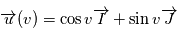$\overrightarrow{u}(v) = \cos v \overrightarrow{I} + \sin v \overrightarrow{J}$ , donc 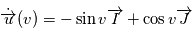$\dot{\overrightarrow{u}}(v) = -\sin v \overrightarrow{I} + \cos v \overrightarrow{J}$ en remplaçant dans, 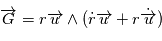$\overrightarrow{G} = r \overrightarrow{u} \wedge (\dot{r}\overrightarrow{u}} + r \dot{\overrightarrow{u}})$ on obtient:

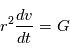
$r^2 \frac{dv}{dt}=G$

Cette équation s'appelle la Loi des aires et signifie que 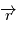$\overrightarrow{r}$ balaie les aires à vitesse constant 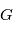. En particulier l'aire totale de l'ellipse est parcourue en un certain temps 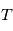fixe: le mouvement est périodique. L'aire de l'ellipse vaut:

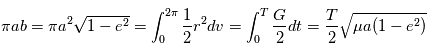
$\pi a b = \pi a^2 \sqrt{1-e^2} = \int_{0}^{2\pi} \frac{1}{2} r^2 dv = \int_{0}^T \frac{G}{2}dt = \frac{T}{2} \sqrt{\mu a (1-e^2)}$

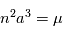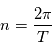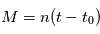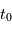On retrouve bien la troisième loi de Kepler : $n^2 a^3 = \mu$ avec $n = \frac{2 \pi}{T}$ . On définit alors l'anomalie moyenne par M = n(t-t_0) où t_0 est le temps de passage au périastre ( 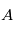sur la figure), qui est proportionnelle à l'aire 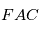FAC (voir figure).