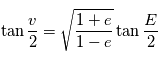Solutions en fonction du temps

Auteur: Nathan Hara & Jacques Laskar

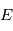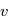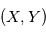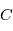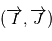Il reste à trouver une relation entre et , ce qui s'obtient aisément en exprimant la position (X,Y) de dans le plan $(\overrightarrow{I}, \overrightarrow{J})$ :

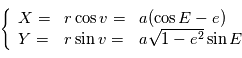
$\left\{ \begin{array}{l l l} X =& r \cos v =& a(\cos E - e) \\ Y =& r \sin v =& a \sqrt{1-e^2} \sin E\end{array}$

On en déduit les relations utiles: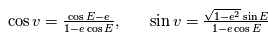 $\begin{array}{l l} \cos v = \frac{\cos E - e}{1 - e \cos E}, \quad & \sin v = \frac{\sqrt{1-e^2} \sin E}{1 - e \cos E} \end{array}$

A ce point, rappelons que l'objectif est d'exprimer la position et la vitesse de l'étoile comme des observables. En exprimant 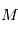en fonction de 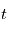puis 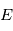en fonction de 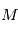on a la position du corps à un instant quelconque. En ce qui concerne l'astrométrie, on peut s'arrêter aux équations ci-dessus et simplement faire un changement de référentiel, c'ést à dire exprimer la projection de 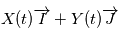$X(t)\overrightarrow{I} + Y(t)\overrightarrow{J}$ sur la sphère céleste et choisir un jeu de paramètres 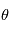$\theta$ à ajuster. Pour les vitesses radiales nous avons besoin de 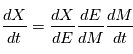$\frac{dX}{dt} = \frac{dX}{dE} \frac{dE}{dM} \frac{dM}{dt}$ . En dérivant l'équation de Kepler par rapport à 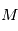on obtient:

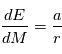
$\frac{dE}{dM} = \frac{a}{r}$

D'où:

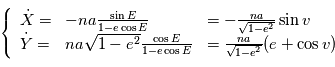
$\left\{ \begin{array}{l l l} \dot{X} =& -na\frac{\sin E}{1-e \cos E} &= -\frac{na}{\sqrt{1-e^2}} \sin v \\ \dot{Y} =& na\sqrt{1-e^2}\frac{\cos E}{1-e \cos E} &= \frac{na}{\sqrt{1-e^2}} (e+\cos v) \end{array}$

En pratique, il n'est pas nécessaire de calculer 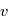en fonction de 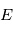. Les expressions ci-dessus suffisent. Pour mémoire, en remplaçant 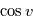$\cos v$ dans la formule trigonométrique 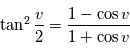$\tan^2 \frac{v}{2} = \frac{1-\cos v}{1+\cos v}$ , on obtient:

$\tan \frac{v}{2} = \sqrt{\frac{1+e}{1-e}} \tan \frac{E}{2}$