Equation de Newton
Les planètes et l'étoile ont un certain volume. Cependant, on peut montrer que lorsque la distance entre deux corps en intéraction gravitationnelle augmente, leur comportement se rapproche de plus en plus de celui de deux points matériels. On néglige aussi les effets relativistes, de sorte que l'on est ramené à la modélisation de l'intéraction de deux points matériels, dont la résolution va suivre.
Considérons deux points matériels 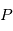 (planète) et
(planète) et 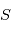 (pour "star" de sorte à éviter un conflit de notation avec l'anomalie excentrique
(pour "star" de sorte à éviter un conflit de notation avec l'anomalie excentrique 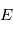 ) de masses respectives
) de masses respectives 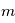 et
et 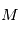 et
et 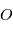 l'origine d'un repère Galiléen. Le principe fondamental de la dynamique s'écrit:
l'origine d'un repère Galiléen. Le principe fondamental de la dynamique s'écrit:
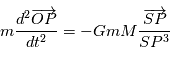 où
où 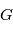 est la constante universelle de gravitation.. En posant
est la constante universelle de gravitation.. En posant 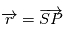 et
et 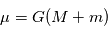 on obtient:
on obtient:
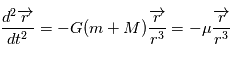
On va montrer que la solution de cette équation décrit une conique plane, une ellipse dans le cas des planètes liées à une étoile. On suppose que le système est isolé, on peut donc choisir comme origine du repère le barycentre du système, ce qui permet d'obtenir facilement 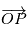 et
et 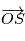 par la relation
par la relation 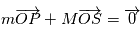 .
.
On suppose que le système est isolé, donc le mouvement du barycentre du système {Etoile+planètes} est rectiligne uniforme dans un référentiel galiléen (par exemple le référentiel barycentrique du système solaire).
Quantités conservées
L'équation de Newton est une équation différentielle de degré deux sur des vecteurs de 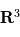 . Pour la résoudre il faut trouver six quantités conservées au cours du mouvement (ou intégrales premières du mouvement) indépendantes. En l'occurrence on peut facilement montrer que deux vecteurs sont conservés au cours du mouvement (ce qui fait deux fois trois composantes, on a bien six scalaires conservés).
Notons
. Pour la résoudre il faut trouver six quantités conservées au cours du mouvement (ou intégrales premières du mouvement) indépendantes. En l'occurrence on peut facilement montrer que deux vecteurs sont conservés au cours du mouvement (ce qui fait deux fois trois composantes, on a bien six scalaires conservés).
Notons  , où
, où 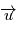 est un vecteur unitaire (et donc
est un vecteur unitaire (et donc 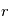 est la norme de
est la norme de 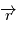 ) et
) et 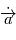 la dérivée par rapport au temps d'un vecteur
la dérivée par rapport au temps d'un vecteur 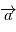 .
On a la conservation du moment cinétique par unité de masse
.
On a la conservation du moment cinétique par unité de masse 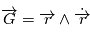 et du vecteur excentricité
et du vecteur excentricité 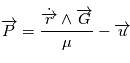 au cours du mouvement c'est à dire leur dérivée temporelle est nulle
au cours du mouvement c'est à dire leur dérivée temporelle est nulle
En effet, soit 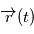 une solution de l'équation de Newton. Alors
une solution de l'équation de Newton. Alors 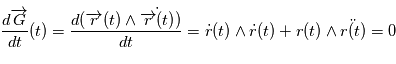 car d'après l'équation de Newton,
car d'après l'équation de Newton, 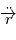 est colinéaire à
est colinéaire à 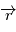 . D'autre part,
. D'autre part, 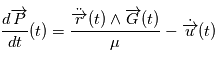 , or
, or
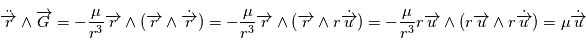
Donc  .
.
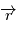 .
.
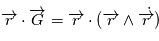 et comme
et comme 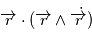 est un produit mixte, il est invariant par permutation circulaire:
est un produit mixte, il est invariant par permutation circulaire: 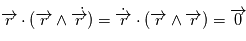 car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur
car le produit vectoriel de deux vecteurs colinéaires est nul. Le vecteur 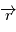 est orthogonal à
est orthogonal à 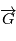 à tout instant, autrement dit le mouvement est dans un plan orthogonal à
à tout instant, autrement dit le mouvement est dans un plan orthogonal à 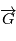 .
.
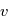 l'angle entre
l'angle entre 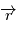 et
et 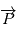 et posons
et posons 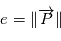 . Alors comme
. Alors comme 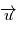 est unitaire,
est unitaire, 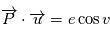 d'autre part en remplaçant
d'autre part en remplaçant 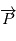 par sa définition, on a
par sa définition, on a 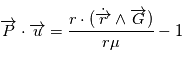 et comme
et comme 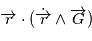 est un produit mixte,
est un produit mixte, 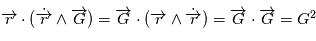 . où
. où 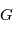 est la norme de
est la norme de 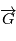 . On obtient alors
. On obtient alors 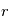 en fonction de
en fonction de 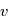 :
:
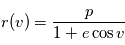
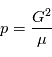 , qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de
, qui est l'équation polaire d'une conique du plan. Cette équation donne une paramétrisation de la solution en fonction de 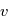 , appelée
, appelée 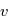 et le temps.
On sait que lorsque
et le temps.
On sait que lorsque 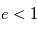 , il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que
, il s'agit de l'équation d'une ellipse. On peut montrer géométriquement que 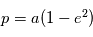 où
où 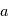 est le demi-grand axe de l'ellipse. Si
est le demi-grand axe de l'ellipse. Si 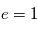 ou
ou 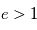 , la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
, la trajectoire est respectivement parabolique ou hyperbolique. Dans ces deux cas le mouvement n'est pas borné, il concernerait une planète en phase d'éjection, événement dont l'observation est très improbable et indiscernable d'une planète à très longue période ou du mouvement propre sur les données actuelles.
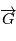 , et le vecteur
, et le vecteur 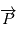 est parallèle à
est parallèle à 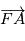 . Notons
. Notons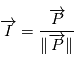 et
et 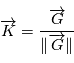 . On introduit un vecteur
. On introduit un vecteur 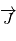 de sorte que
de sorte que 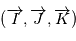 forme une base orthonormale.
forme une base orthonormale.
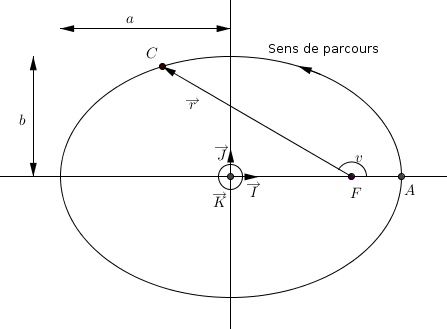
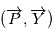
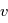 , angle entre le vecteur excentricité et le vecteur
, angle entre le vecteur excentricité et le vecteur 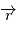 .
.
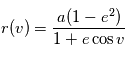
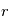 en fonction du temps on va introduire successivement deux variables,
en fonction du temps on va introduire successivement deux variables, 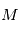 et
et 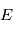 appelées respectivement '
appelées respectivement '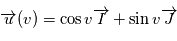 , donc
, donc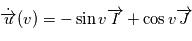 en remplaçant dans,
en remplaçant dans, 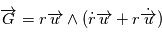 on obtient:
on obtient:
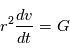
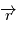 balaie les aires à vitesse constant
balaie les aires à vitesse constant 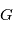 . En particulier l'aire totale de l'ellipse est parcourue en un certain temps
. En particulier l'aire totale de l'ellipse est parcourue en un certain temps 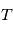 fixe: le mouvement est périodique. L'aire de l'ellipse vaut:
fixe: le mouvement est périodique. L'aire de l'ellipse vaut:
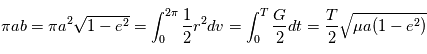
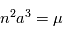 avec
avec 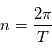 . On définit alors l'
. On définit alors l'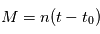 où
où 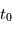 est le temps de passage au périastre (
est le temps de passage au périastre (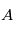 sur la figure), qui est proportionnelle à l'aire
sur la figure), qui est proportionnelle à l'aire 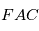 (voir figure).
(voir figure).
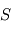 et
et 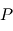 de masses respectives
de masses respectives 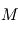 et
et 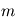 . On pose
. On pose 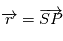 ,
, 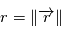 et
et 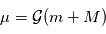 où
où 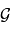 est la constante universelle de gravitation.
est la constante universelle de gravitation.
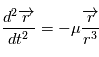
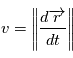 . Déduire du théorème de l'énergie mécanique que
. Déduire du théorème de l'énergie mécanique que 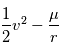 est une quantité constante au cours du mouvement
est une quantité constante au cours du mouvement 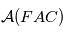 est proportionnelle à l'anomalie moyenne
est proportionnelle à l'anomalie moyenne 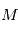 .
.
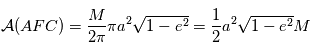
 de rapport
de rapport 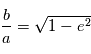 . Donc
. Donc
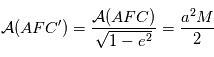
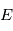 l'angle
l'angle 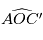
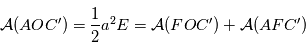
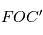 s'obtient facilement car
s'obtient facilement car 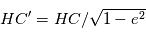
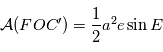
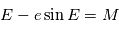
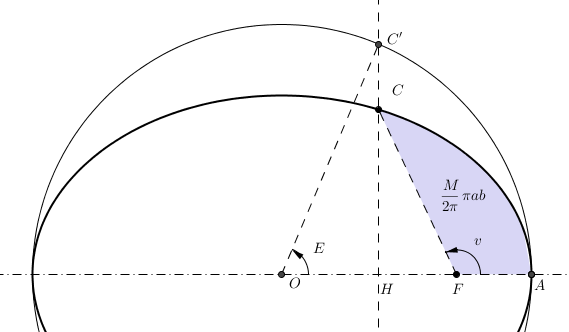
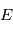 en fonction de
en fonction de 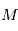 . Cependant, on peut développer
. Cependant, on peut développer 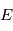 en puissances de
en puissances de 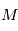 .
.
 , excentrique
, excentrique 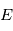 et moyenne
et moyenne 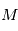 .
.
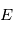 et
et 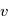 , ce qui s'obtient aisément en exprimant la position
, ce qui s'obtient aisément en exprimant la position 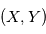 de
de 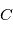 dans le plan
dans le plan 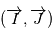 :
:
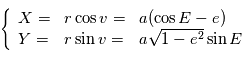
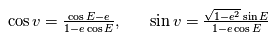
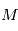 en fonction de
en fonction de 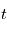 puis
puis 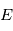 en fonction de
en fonction de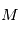 on a la position du corps à un instant quelconque. En ce qui concerne l'astrométrie, on peut s'arrêter aux équations ci-dessus et simplement faire un changement de référentiel, c'ést à dire exprimer la projection de
on a la position du corps à un instant quelconque. En ce qui concerne l'astrométrie, on peut s'arrêter aux équations ci-dessus et simplement faire un changement de référentiel, c'ést à dire exprimer la projection de 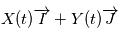 sur la sphère céleste et choisir un jeu de paramètres
sur la sphère céleste et choisir un jeu de paramètres 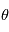 à ajuster. Pour les vitesses radiales nous avons besoin de
à ajuster. Pour les vitesses radiales nous avons besoin de 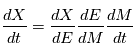 . En dérivant l'équation de Kepler par rapport à
. En dérivant l'équation de Kepler par rapport à 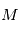 on obtient:
on obtient:
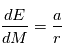
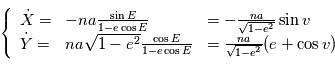
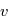 en fonction de
en fonction de 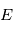 . Les expressions ci-dessus suffisent. Pour mémoire, en remplaçant
. Les expressions ci-dessus suffisent. Pour mémoire, en remplaçant 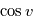 dans la formule trigonométrique
dans la formule trigonométrique 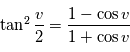 , on obtient:
, on obtient:
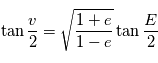
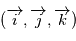 où
où 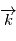 est la direction d'observation et
est la direction d'observation et 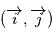 sont choisis de sorte que le repère est orthonormé direct. Le repère
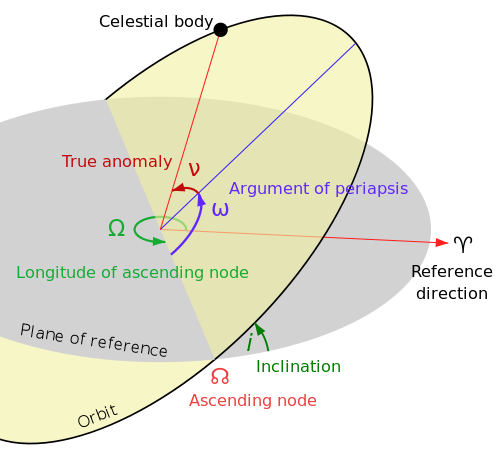
sont choisis de sorte que le repère est orthonormé direct. Le repère 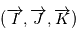 est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
est lui aussi orthormé direct. La matrice de passage du repère orbital au repère d'observation est donc une rotation, que l'on décompose en trois rotations dont les angles ont des noms usuels.
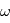 d'axe
d'axe 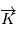 (parallèle au moment cinétique), cet angle est appelé
(parallèle au moment cinétique), cet angle est appelé 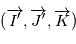 .
. 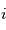 d'axe
d'axe 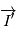 , c'est l'
, c'est l' 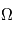 d'axe
d'axe 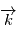 , c'est l'
, c'est l'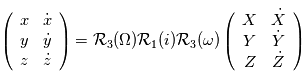
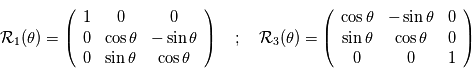
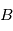 le barycentre du système {planète+étoile}, on note
le barycentre du système {planète+étoile}, on note 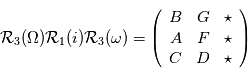 où
où 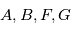 sont appelées les
sont appelées les 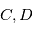 n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que
n'est en revanche qu'une convention pour ce cours et ne se trouve pas spécialement dans la littérature. On ne donne pas de nom particulier aux éléments de la dernière colonne de la matrice car étant donné que 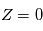 , ils n'apparaissent jamais dans les calculs
, ils n'apparaissent jamais dans les calculs
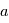 : le demi-grand axe
: le demi-grand axe 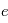 : l'excentricité
: l'excentricité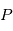 : la période
: la période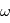 : l'argument du périastre
: l'argument du périastre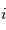 : l'inclinaison
: l'inclinaison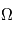 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant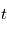 donné, il faut de plus connaître l'instant de son passage au périastre
donné, il faut de plus connaître l'instant de son passage au périastre 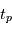 . On peut alors calculer
. On peut alors calculer 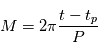 connaisant
connaisant 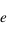 on peut calculer l'anomalie excentrique
on peut calculer l'anomalie excentrique 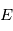 par l'équation de Kepler, puis l'anomalie vraie
par l'équation de Kepler, puis l'anomalie vraie 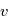 . On en déduit la position sur l'ellipse par l'équation donnée page
. On en déduit la position sur l'ellipse par l'équation donnée page 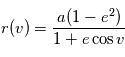 . Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.
. Enfin, la position sur l'orbite est donnée par les rotations explicitées ci-dessus.
 , le mouvement de l'étoile
, le mouvement de l'étoile 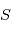 en fonction du temps peut s'écrire:
en fonction du temps peut s'écrire:
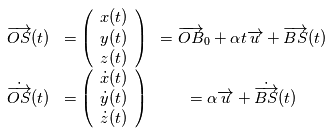
 est la position du barycentre
est la position du barycentre  du système {Etoile, Planète} à
du système {Etoile, Planète} à 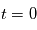 ,
, 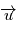 est la direction du mouvement de
est la direction du mouvement de 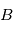 et
et 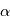 son module.
son module.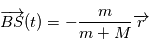 où
où 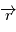 vérifie
vérifie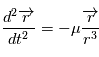 , qui est une équation différentielle de degré deux sur l'espace. Lorsque
, qui est une équation différentielle de degré deux sur l'espace. Lorsque 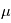 est fixé et la position et la vitesse à
est fixé et la position et la vitesse à 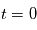 ,
, 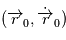 sont connus, la position et la vitesse sont données par le flot:
sont connus, la position et la vitesse sont données par le flot: 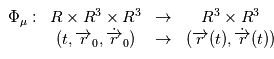 . En d'autres termes, les sept paramètres
. En d'autres termes, les sept paramètres 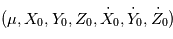 définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple
définissent une orbite de manière univoque. On peut faire un changement de variables pour décrire l'orbite par un autre jeu de sept paramètres, par exemple 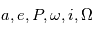 et
et 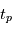 , qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
, qui sont les paramètres classiques présentés dans la section précédente. La plupart des auteurs les utilisent pour ajuster le mouvement des planètes, mais ils ont l'inconvénient d'être très sensibles aux erreurs pour de faibles excentricités et inclinaisons. Pour palier à ce problème on définit:
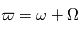 : la longitude du périhélie
: la longitude du périhélie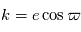
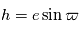
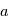 : le demi-grand axe
: le demi-grand axe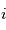 : l'inclinaison
: l'inclinaison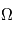 : l'ascension droite au noeud ascendant
: l'ascension droite au noeud ascendant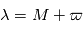 : la longitude
: la longitude