| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Bruits |
Dans le modèle 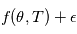 , le symbole
, le symbole 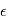 désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
A une expérience donnée, 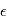 prendra une valeur
prendra une valeur 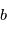 imprévisible. La probabilité que la valeur de
imprévisible. La probabilité que la valeur de 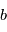 soit comprise entre
soit comprise entre 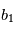 et
et 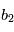 est
est 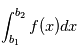 où
où 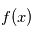 est la densité de probabilité de
est la densité de probabilité de 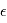 . Dire que
. Dire que 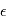 est un bruit gaussien veut dire que sa densité est de la forme
est un bruit gaussien veut dire que sa densité est de la forme 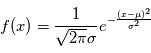 où
où 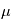 et
et 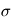 sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de
sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de 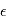 . On note souvent
. On note souvent 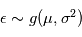 , qui signifie "
, qui signifie "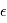 suit une loi gaussienne de moyenne
suit une loi gaussienne de moyenne 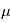 et de variance
et de variance 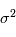 . Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
. Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
Dans le modèle, des bruits d'origines différentes s'additionnent. Sachant que le résidu de l'activité stellaire que nous n'avons pas ajusté 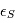 et le bruit de mesure
et le bruit de mesure 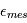 suiven une certaine loi, quelle loi suivra
suiven une certaine loi, quelle loi suivra 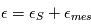 ? Nous pouvons déjà dire que la moyenne de
? Nous pouvons déjà dire que la moyenne de 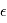 sera égale à la somme des moyennes de
sera égale à la somme des moyennes de 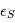 et
et 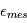 car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de
car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de 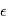 est égale à la somme des variances de
est égale à la somme des variances de 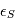 et
et 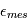 . Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé,
. Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé, 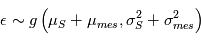 en l'occurrence
en l'occurrence 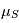 et
et 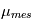 sont nulles.
sont nulles.
Lorsqu'on dispose de plusieurs mesures, à l'expérience numéro 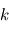 on a un certain bruit
on a un certain bruit 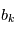 réalisation d'une variable
réalisation d'une variable 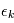 de densité
de densité 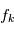 . La plupart du temps, on fait l'hypothèse que les brutis
. La plupart du temps, on fait l'hypothèse que les brutis 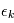 sont indépendants, c'est à dire que la probabilité d'obtenir le bruit
sont indépendants, c'est à dire que la probabilité d'obtenir le bruit 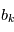 à l'expérience
à l'expérience 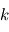 ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur densité spectrale de puissance. Un certain profil de densité spectrale correspond à une "couleur" du bruit.
ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur densité spectrale de puissance. Un certain profil de densité spectrale correspond à une "couleur" du bruit.
A retenir: la somme de variables gaussienne indépendantes 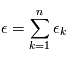 où
où 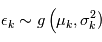 est une variable gaussienne suivant la loi
est une variable gaussienne suivant la loi 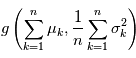 .
.