| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Processus stochastique et Densité spectrale de puissance |
La notion de densité spectrale de puissance (DSP) n'est pas simple à définir, cependant très utilisée dans la littérature de traitement du signal. Nous donnons une définition mathématique pour qu'il n'y ait pas d'ambiguités mais compte tenu de la sophistication des notions introduites, le lecteur pourra se référer à la description qualitative suivante.
La densité spectrale de puissance est une propriété relative à plusieurs variables aléatoires. Les familles de variables aléatoires peuvent par exemple représenter des mesures sur lesquelles on a une incertitude. A chaque instant de mesure on associe une variable alétoire qui a une certaine densité de probabilité. En physique théorique ou en économie, on rencontre des processus stochastiques continus - typiquement le mouvement brownien, qui représente des mouvements d'atomes ou des fluctuations de prix. Formellement, un processus stochastique est une famille de variables aléatoires indexées par un ensemble totalement ordonné 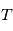 , toutes définies sur le même espace de probabilité (
, toutes définies sur le même espace de probabilité (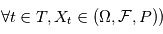 . Dans ce cours on aura seulement besoin de
. Dans ce cours on aura seulement besoin de 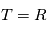 ou
ou 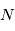 . On note
. On note 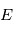 l'espérance mathématique.
l'espérance mathématique.
Dans le cas général, la densité de probabilité de la variable aléatoire 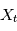 (pour
(pour 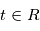 ) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que
) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que 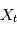 vaut une certaine valeur réelle
vaut une certaine valeur réelle 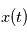 avec la probabilité 1, la DSP en une fréquence
avec la probabilité 1, la DSP en une fréquence 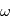 est égale à
est égale à 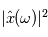 , où
, où 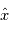 est la transformée de Fourier de
est la transformée de Fourier de 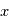 . Si maintenant
. Si maintenant 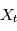 est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de
est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de 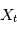 .
.
Pour définir cette notion mathématiquement, on doit d'abord introduire les notions de convergences et intégrales en moyenne quadratique. Pour plus de précision le lecteur peut se référer au cours de Timo Koski à KTH.
Rappelons d'abord que si 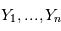 sont des variables aléatoires et
sont des variables aléatoires et 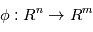 une fonction mesurable alors
une fonction mesurable alors 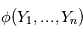 est une variable aléatoire. En particulier, si
est une variable aléatoire. En particulier, si 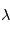 est un scalaire,
est un scalaire, 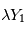 et
et 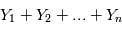 sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.
Soit 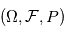 un espace de probabilités, on dit que la suite de variables aléatoires
un espace de probabilités, on dit que la suite de variables aléatoires 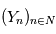 telle que
telle que 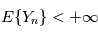 , définies sur cet espace converge en moyenne quadratique si et seulement si:
, définies sur cet espace converge en moyenne quadratique si et seulement si:
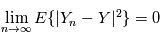
Soit 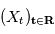 un processus stochastique continu (
un processus stochastique continu (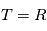 ) tel que chacune des variables aléatoires
) tel que chacune des variables aléatoires 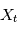 a une espérance finie (
a une espérance finie (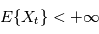 ). L'intégrale en moyenne quadratique du processus
). L'intégrale en moyenne quadratique du processus 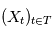 sur l'intervalle
sur l'intervalle ![[a,b]](../pages_ind-vr/equations_etoile/equation44.png) est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:
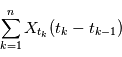
Pour 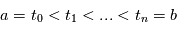 et
et 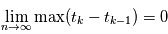 . On la note alors
. On la note alors 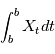 .
.
On définit alors la densité spectrale de puissance comme:
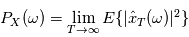
Où 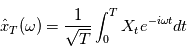
Cette définition un peu complexe peut être vue comme une généralisation de la transformée de Fourier à des processus stochastiques. En effet, lorsque le processus 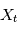 est telle que
est telle que 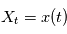 avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors
avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors 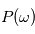 est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle
est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle 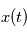 . Dans le cas où les
. Dans le cas où les 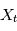 sont aléatoire,
sont aléatoire, 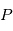 est le carré de la transformée de Fourier "en moyenne" des réalisations de
est le carré de la transformée de Fourier "en moyenne" des réalisations de 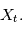 Par exemple si
Par exemple si 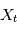 modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant
modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant 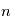 profils de tension
profils de tension 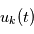 à l'expérience
à l'expérience 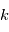 (des réalisations du processus stochastique
(des réalisations du processus stochastique 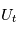 ), la moyenne des carrés du module des transformées de Fourier des
), la moyenne des carrés du module des transformées de Fourier des 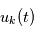 notée
notée 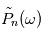 sera approximativement égal à
sera approximativement égal à 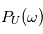 . Si le nombre d'expérience
. Si le nombre d'expérience 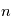 tend vers l'infini
tend vers l'infini 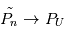 en norme 2.
en norme 2.
Dans le cas d'un processus stationnaire discret (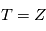 ), on peut directement définir
), on peut directement définir 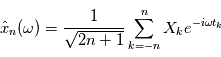 et
et 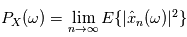 .
.
La densité spectrale de puissance a une définition plus simple lorsque le processus est stationnaire, c'est à dire lorsque le processus 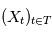 vérifié:
vérifié:
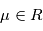 tel que
tel que 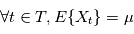
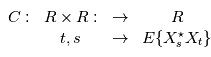 ne dépend que de
ne dépend que de 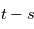 , i. e.
, i. e. 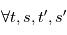 tels que
tels que 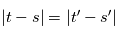 , on a
, on a 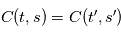 . On note appelle alors habituellement la fonction d'autocorrélation
. On note appelle alors habituellement la fonction d'autocorrélation 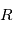 , telle que
, telle que 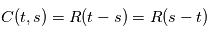
Les processus stationnaires modélisent des phénomènes qui ont une certaine invariance dans le temps, en particulier la covariance ne dépend pas de 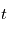 de manière absolue, mais de manière relative à un autre instant. Dans ce cas, la densité spectrale de puissance est égale au carré du module de la transformée de Fourier de la fonction
de manière absolue, mais de manière relative à un autre instant. Dans ce cas, la densité spectrale de puissance est égale au carré du module de la transformée de Fourier de la fonction 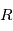 . L'équivalence avec la définition de la densité spectrale de puissance donnée plus haut est établie par le théorème de Wiener-Khinchin.
. L'équivalence avec la définition de la densité spectrale de puissance donnée plus haut est établie par le théorème de Wiener-Khinchin.